数学家的“数学”墓碑（上）

墓碑是人们用来纪念逝去之人的标志，上面往往记载着墓主一生的经历与功过。大到帝王将相，小到百姓庶民，去世后使用墓碑供后人景仰或祭奠，并不足为奇；耐人寻味的是，大凡数学家留下的墓志铭都言简意赅，也最发人深省。下面，就向大家介绍几位著名数学家的墓碑。

阿基米德的墓碑

阿基米德是古希腊杰出的数学家（图1），也是举世公认的最伟大的数学家之一，其贡献大大超越了他所处的时代，因而在数学史上占有重要地位，他与牛顿、高斯三人同为历史上最伟大的数学家。值得一提的是，阿基米德对数学的执着赢得了全世界的尊重。

公元前212年，古罗马军队入侵叙拉古（又被译为锡拉库萨，在今意大利西西里岛）。在阿基米德的倾力相助下，叙拉古城得以坚守三年之久才失陷。城破之时，75岁的阿基米德还在潜心研究画在沙盘上的几何图形。破城而入的罗马士兵闯入了阿基米德的房间，举剑向他刺去。在生命的最后时刻，阿基米德还在大喊：“不要动我的图！”令人遗憾的是，这位粗鄙的罗马士兵并不认识声名显赫的阿基米德，刀剑挥处，伟大的数学家倒在了血泊里。

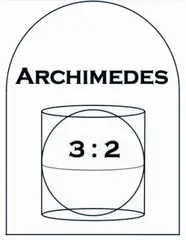
得知阿基米德被杀，统帅罗马大军的将军马塞拉斯痛惜万分，不仅处决了凶手，而且为阿基米德举行了隆重的葬礼，并建造陵墓，以示敬仰。137年后的公元前75年，时任西西里市政官的著名政治家、哲学家西塞罗游历叙拉古时，慕名前往阿基米德墓，发现陵墓早已湮没于荒草之中。众人开出一条小路，最终发现一座坟墓，被风雨侵蚀的墓碑上只依稀可见“圆柱内切球”这个几何图形（图2）。此图形是在圆柱体内放置一个圆球，该球可谓“顶天立地”，四周碰边。为什么阿基米德的墓碑上会刻着这样一个图形呢？

原来，阿基米德一生中发现了许多定理，他本人最得意的就是有关圆柱体和球的体积定理：如果在圆柱内有一个直径与圆柱体等高的内切球，则球的表面积和体积分别等于圆柱体的表面积和体积的三分之二。阿基米德希望在他死后，把一生中最引以为豪的“球内切于圆柱”的图形刻在自己的墓碑上。当年建造阿基米德墓时，罗马将军马塞拉斯之所以这样做，正是为了表达对阿基米德的钦佩和尊敬。

见到此图，西塞罗非常激动，感慨不已，同时命人修复了阿基米德墓。可惜的是，2000多年的岁月流逝，使得阿基米德墓再次湮没于历史长河中。1965年，叙拉古一家在建的饭店挖掘地基时，挖出过一块石碑，上面刻着一个内切于圆柱体的圆球的图形，不过，人们并不能确定此处就是阿基米德墓。如今，我们只知道阿基米德的墓碑上刻有“圆柱内切球”几何图形，但并没有找到实物。当然，这丝毫不影响这一数学定理成果广为人知。

丢番图的墓碑

丢番图是古希腊著名的数学家（图3），以高超的解题技巧著称。他的著作《算术》是一本非常有名的数学问题集，具有高度的创造性；可惜的是，这部著作未能完整地保存下来，现仅存6卷（原书共有13卷）。《算术》一书第一次系统地使用代数符号，提出了各种不定方程的巧妙解法，在数学史上被称为“代数的开山之作”。自毕达哥拉斯学派之后，数学的理论系统一直披着几何的外衣；但丢番图的数学思想完全脱离了几何形式，将代数从中解放出来，自成体系，成为单独的学科。这在古希腊数学史上可谓独树一帜。因此，丢番图被誉为“代数学的鼻祖”。

丢番图的著作成为包括费马、欧拉、高斯等在内的许多数学家进行数论研究的起点。比如，著名的费马大定理就是费马在阅读《算术》第二卷命题8时在页边写下的批语。谁能想到，这寥寥数语竟然令跨越了几个世纪的无数数学家折腰。

关于丢番图的生平，后人几乎一无所知，他唯一的简历是《希腊诗文选》（The Greek Anthology）中麦特罗尔写的有关丢番图的墓碑（图4），上面用诗歌的形式写成一段谜一样的碑文，使我们可以对丢番图的一生有一个大略了解。碑文如下：“过路的人啊！这里埋着丢番图。下面的数字多么令人惊讶，它忠实地记录了丢番图一生的坎坷历程。他生命的1/6是幸福的童年；再活了一生的1/12，他的唇上长出了细细的胡须；其后，丢番图结婚了，可是还不曾有孩子；这样又度过了一生的1/7。再过5年，他有了一个儿子，感到很幸福，可是这个孩子的寿命只有他父亲的一半。儿子死后，这位老人在深深的悲痛中又活了4年，才结束其尘世生涯。”

显然，该碑文实际上是一道蕴含深意的数学题，它让人们在祭奠之时不免思索、计算丢番图的年龄，感慨这位数学家是至死也离不开数学的“另类”。

鲁道夫和欣克斯的墓碑

众所周知，古今中外的数学家一直为了求得圆周率精度较高的准确值而不断努力。公元前3世纪，古希腊著名学者阿基米德最先得出π≈3.14。到公元150年左右，古希腊天文学家托勒密最先给出π小数点后4位的准确值；在263年前后，我国魏晋时期的数学家刘徽利用割圆术也求得π≈3.1416。在480年前后，我国南北朝时期杰出的数学家祖冲之最早确定出π小数点后7位的准确值，即π介于3.1415926和3.1415927之间，这个数值保持世界纪录近1000年。

直到1424年，阿拉伯数学家阿尔·卡西计算出π=3.141592653589793251596，才打破祖冲之的纪录。16世纪，荷兰籍德国人鲁道夫·范·科伊伦加入竞争行列，他通过计算圆外切与圆内接正230边形，将π值精确到小数点后15位。后来，他把正多边形的边数增加到262，于1610年算出π的35位小数，一举创造了新的世界纪录。这一工作几乎耗费了鲁道夫（图5）的毕生心血，他为自己不虚此生而自豪，并留下遗言：将精确到小数点后35位的π值刻在他的墓碑上。于是，鲁道夫的墓碑上铭刻着：π≈3.14159 26535 89793 23846 26433 83279 50288（图6）。

随后，π的准确数值纪录一次次被刷新：1706年，人们计算出的π的小数点后数值越过百位大关；1842年，达到了200位；1854年，突破400位……英国数学家威廉·欣克斯采用无穷级数的方法，经过20年不懈努力，于1973年将π算到惊人的707位小数。在电子计算机问世之前，这可算得上是手工演算时代的最高纪录。欣克斯自认无人可比，并以此为荣，还嘱托家人，在他死后将这一结果刻在墓碑上。此后半个世纪，人们对欣克斯的计算结果深信不疑，以致在1937年巴黎世界博览会的发现馆中，依然在最明显的地方刻着这个π值。

令人悲哀的是，到了1945年，英国数学家弗格森发现，欣克斯的π值的第528位小数值有误，应为4，结果误为5，这意味着之后的数值全都是错的。一个小小的疏忽让欣克斯白白浪费了十多年的光阴，实在令人惋惜，但这并不能否定欣克斯在特定年代、特定环境下所做出的表率和贡献。

莱布尼茨的墓碑

莱布尼茨是德国最著名也最重要的自然科学家、物理学家、历史学家、哲学家，他和牛顿同为独立发明微积分的创始人（图7）。这位举世罕见、才华横溢的科学全才，对丰富人类科学知识宝库做出了不可磨灭的贡献，被誉为“17世纪的亚里士多德”。

莱布尼茨生于莱比锡，自幼丧父的他博览群书，涉猎广泛，对语言、古典文学、史学、法律、逻辑学和哲学等诸多学科都有着浓厚的学习兴趣。这使得莱布尼茨思想活跃，不盲从，有主见。年仅20岁时，他就写出了题为《论组合的技巧》的论文，创立了关于“普遍特征”的“通用代数”，即数理逻辑的新思想。随后，莱布尼茨还与英国数学家、物理学家牛顿分别独立地创立了微积分学，其严密性与系统性比牛顿更胜一筹。他所创设的微积分符号也远优于牛顿创设的符号，因而被数学界和数学教材普遍接受及广泛使用。

更值得一提的是，莱布尼茨是第一位认识到二进制记数法重要性的人，并系统地提出了二进制数的运算法则。尽管欧美数学家都认为，二进制记数法的诞生应归功于莱布尼茨，但事实上，莱布尼茨并不是这种记数法的发明人。在他之前，已经有人提出过这种记数法：17世纪初，英国代数学家哈里奥特在其未发表的手稿中提到了该方法；1670年，意大利数学家卡瓦利埃里又一次重复了这一发现。莱布尼茨重新发现二进制的时间是在1672年至1676年。1679年3月15日，他撰写了题为《二进算术》的论文，对二进制进行了充分的论述，并建立了二进制的表示及运算。

在他看来，一切数都可以由0和1创造出来，这正可以作为《圣经》所说上帝从“无”创造“有”的象征。也就是说，从二进制中，莱布尼茨发现了“上帝创造世界”的证据。莱布尼茨的这些研究结果表明，他并未借助前人的论述和研究，而是独立发现了二进制。正是在他的大力提倡和阐述下，二进制才逐渐被人们普遍关注。从某种意义上说，把二进制与莱布尼茨联系在一起，也无不妥之处。

1701年，莱布尼茨将关于二进制的论文提交给法国科学院，但要求暂不发表。两年后，也就是1703年，他将修改后的论文再次送交法国科学院，并要求公开发表。自此，二进制开始被公之于众。如今，时代和科技的发展已经用事实证明，二进制对于200多年后计算机的发展产生了深远的影响，莱布尼茨也因极具前瞻性的研究名垂青史。

牛顿的墓碑

伊萨克·牛顿是英国著名的物理学家、数学家（图9），百科全书式的“全才”，在影响人类历史人物风云榜上始终位列前茅。

1661年，牛顿考入著名的剑桥大学。1665年，从大学毕业的牛顿正准备留校继续深造之时，恰逢鼠疫席卷英国，牛顿被迫两次回到故乡避灾，这恰恰是牛顿一生中最重要的转折点。在家乡安静的环境里，牛顿专心致志地思考数学、物理学和天文问题。在短短18个月里，牛顿就孕育形成了流数术（微积分）、万有引力定律和光学分析的基本思想。这时的他不过23岁。

1684年，牛顿通过计算完善了1666年发现的万有引力。1687年，他完成了人类科学史上少有的科学巨著《自然哲学的数学原理》，用数学方法建立起完整的经典力学体系，轰动全世界。法国科学家拉普拉斯评价该书为“人类智慧产物中最卓越的杰作”。