一种高精度星敏感器抗地气光星图预处理算法

摘要：      近地空间飞行器所搭载的星敏感器易受地气光影响， 导致星点提取精度较低进而影响天文导航的精度。 针对这一问题， 本文提出了一种高精度的抗地气光星图预处理算法。 通过分析地气光的传播机理， 建立地球大气散射以及地表反射模型， 构建了一种精确的地气光辐射强度模型。 通过分析星敏感器像面上局部范围内所接收地气光的传输路径与像素坐标之间的关系， 对辐射强度模型进行变换得到了局部邻域内的地气光背景灰度模型， 进而利用背景估计法实现对地气光影响下的杂散光背景的精确估计与补偿。 最后， 通过仿真以及实拍星图对算法性能进行验证， 结果表明所设计算法能有效提升星图信噪比以及质心提取精度， 并且具有较好的抗干扰能力。

关键词：     星敏感器； 地气光； 大气散射； 背景估计； 星图预处理; 导航

中图分类号：     TJ760; V448    文章编号：     1673-5048（2023）04-0091-07

文献标识码：    A    DOI： 10.12132/ISSN.1673-5048.2022.0224

0引言

星敏感器是一种以恒星作为观测对象的天体敏感器， 具有自主性好、 测量精度高、 无累积误差、 体积和质量小等优势［1］， 在航空航天飞行器上有广泛应用。 星敏感器工作时， 除了接收到目标恒星的辐射能量外， 还会受到太阳光、 月光、 地气光、 地球热等杂散辐射的影响［2］。 其中， 地气光是太阳光经复杂的大气散射及地表反射后形成的［3］， 会在星敏感器像平面上形成非均匀背景灰度， 进而降低像平面的对比度以及恒星的信噪比， 影响星点质心的提取精度及天文导航精度。 因此， 对于近地空间飞行器所搭载的星敏感器而言， 如何消除地气光对星图的影响是天文导航亟待解决的一项关键技术。

目前消除地气光对星图影响的方法有三类： 频域特征消除法、 空间域特征消除法和背景估计消除法。 频域特征消除法是利用星点在频域中呈现的高频特性， 与低频的背景进行区分， 进而去除地气光导致的背景灰度［4-5］。 但由于星图中地气光背景的频谱范围广， 星点与地气光背景在频域上存在混叠［6］， 使得该方法对地气光去除的效果不佳； 由于星点在空间域上表现出“凸起”的特点， 而地气光背景在空间域上变化较为平缓， 因此， 空间域特征消除法是利用星点与地气光背景在空间域上的差异， 使用形态学滤波或灰度前向差分等算法去除地气光背景［7-9］。 但对于地气光影响下的低信噪比星图而言， 星点通常被背景淹没导致其形态特点不显著， 该方法会将星点的部分区域视为背景予以去除， 进而破坏星点的能量分布， 影响质心提取精度； 背景估计消除法是基于局部区域内地气光背景灰度值的相关性， 将背景灰度建模成一个平面， 再利用相邻像素的灰度值对星点处的背景灰度进行估计与补偿［10-12］， 进而消除地气光对星图的影响。 由于星点成像的几何位置集中， 在背景估计时可以通过设计模板对星点进行规避［10，  13］， 使得该算法对星点能像分布的破坏程度较小， 具有较好的预处理效果。 但实际的地气光是经复杂的散射以及反射后形成的， 其在像平面上的分布规律复杂多变， 难以使用平面背景模型对其进行精确描述， 导致对地气光背景的估计精度不佳， 制约了其对地气光背景的去除效果。

本文通过分析太阳光经过地球-大气系统的散射以 及反射，  构建了一种精确的地气光辐射强度模型， 并分析地气光背景灰度在星图中的分布规律， 进而设计了一种基于三次曲面模型的抗地气光星图预处理算法。

1地气光辐射强度模型

地气光会在星敏感器像平面上形成非均匀的背景灰度， 影响星点质心的提取精度及天文导航精度。 为定量分析其在星敏感器像平面上的分布规律， 需建立地气光的辐射强度模型，  以分析像平面上各像素所接收到的地气光辐射强度。

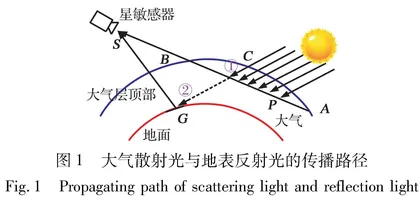
太阳光经过地球大气散射与地表反射作用后形成地气光。 实际上，  由于大气密度随高度和大气层温度变化较大， 受非均匀大气的折射作用， 光线沿曲线传播， 但大气折射所导致的光线偏折角小于38′， 对光线的辐射强度影响及其分布规律影响不大。 因此， 为简化分析过程， 对光线到达星敏感器入瞳平面的路径采用了直线假设， 其传播路径如图1所示。

图中， 路径①为大气散射光的传播路径， 太阳光从大气C处射入， 在大气中P发生散射， 再从A点穿出大气层到达星敏感器入瞳平面S。 路径②为地表反射光的传播路径， 太阳光经大气C处射入， 穿过大气到达地球表面G， 在地表反射后穿出大气层达到星敏感器入瞳平面S。

大气散射光与地表散射光叠加后形成地气光。 为建立地气光的辐射强度模型， 可先分别建立大气散射光与地表散射光的辐射强度模型。

1.1大气散射光辐射强度模型

为建立大气散射光的辐射强度模型， 以一束大气散射光线为例， 其在大气中的传播路径如图2所示。

太阳光从C点射入大气， 在P点以散射角θ发生散射， 散射后光线从A点射出大气。

光线在大气中传输， 受大气的吸收和散射作用后发生衰减， 根据朗伯-比尔定律［13］ ， 可计算得到P点的光线辐射强度为

IP=IsT（CP）（1）

式中： Is为大气表面的太阳光辐射强度； T（CP）是衰减系数， 表示光线在CP路径上传输过程中的衰减程度， 可表示为

式中： β（λ）为散射系数； D（CP）为路径CP的光学距离； ρ（h）为不同高度处的大气密度； s为光线传输路径长度。

光线在P点发生散射， 散射光沿路径PA传播， 经大气影响衰减后从A点射出大气， 其辐射强度为

IPA=IPS（λ，  θ，  h）T（PA）（4）

式中： S为散射方程，  S=β（λ）ρ（h）γ（θ）， γ（θ）为散射的相位函数； T（PA）为光线在路径PA上的衰减系数。

在实际过程中， 太阳光在路径AB上各点都发生了散射， 因此将式（4）的单束散射光在A点的辐射强度沿散射路径AB积分， 可得A点射出的大气散射光辐射强度表示为

式中： l为散射路径长度。

根据A点的大气散射光辐射强度， 可计算得到以不同散射角散射的光线辐射强度。

1.2地表反射光辐射强度模型

太阳照射在地球表面形成阳照区， 阳照区内的地表面元向外反射太阳光， 穿出大气后形成地表反射光。 取地表G点处的面元i进行分析， 在该面元处发生反射的光路如图3所示。

式中： d为日地距离； BRDFi为该地表面元沿着目标方向的双向反射分布函数， 可由参数化的BRDF模型计算得到［15］； 面元i的面积为dAi； θr为反射光与法线的夹角。

反射光线受大气影响衰减后从A点射出大气， 其辐射强度为

exp{－β（λ）［D（CG）+D（GA）］}dAi（9）

综合考虑大气散射效应及地表反射效应， 对式（5）的大气散射光辐射度与式（9）的地表反射光辐射强度求和， 得到从A点处射出大气的地气光辐射强度模型：

IA=IA， s+IA， r（10）

基于式（10）的地气光辐射强度模型， 可探究影响地气光辐射强度的因素， 进而分析地气光背景在星敏感器像平面上的分布规律。

2地气光辐射强度特性分析

地气光由地表反射光与大气散射光共同构成， 但由于地球对导航星的遮挡作用， 地表反射光所影响的星图区域内不存在星像点， 因此地表反射光不会影响星点的成像。 星图中星像点的背景灰度主要由大气散射光所导致， 它是影响星点成像的主要因素， 需对其辐射强度特性进行分析。

如式（5）所示， 大气散射光的辐射强度模型描述为

由于大气的厚度远小于地球半径， 且大气层的曲率较小， 太阳光入射路径CP的长度远小于出射路径PA的长度。 此外， 太阳光入射所处的高度较高， 大气稀薄， 因此， 光线传输过程的光学距离D（CP）远小于D（PA）。 为简化分析过程， 可忽略D（CP）项， 将式（11）简化为

如图4所示， 根据几何关系， 可得散射路径长度的微分dl与散射点高度的微分dh间的关系：

dl=k（hP1－hP2）=kdh （13）

式中： k=secφ， φ为散射路径方向矢量与散射点的位置矢量之间夹角的补角。

由于光线传输路径长度远小于地球半径， 散射路径上各点所对应的φ变化幅度较小， 不超过5°， 可视为常值。 对式（13）积分， 可得散射路径长度l与高度h间的关系， 即

式中： hs为散射路径的高度。

大气密度ρ与高度h近似成指数关系［16］， 即

式中： ρ0为高度h0处的大气密度； H为密度标尺高度。

将式（13）～（15）代入D（PA）， 则

将式（16）代入式（12）中， 并将积分变量散射路径长度l替换为散射高度h可得

由上式可知， 大气散射光的辐射强度可表示为光线波长λ、 散射角度θ以及散射高度hs的函数。

将地球和大气视为理想的球体， 则根据几何关系， 可得散射高度hs和散射路径长度l间的关系， 即

式中： Re为地球半径； datm为地球大气厚度。

由此可将大气散射光辐射强度模型中的f（hs）表示为散射路径长度l的函数f（l）。

对星敏感器而言， 其所能敏感的光线波长固定， 即β（λ）为常数。 令传输系数T（l）=β（λ）f（l）， 则可将大气散射光辐射强度模型改写为

IA， s=Isγ（θ）T（l） （19）

式（19）表示了大气散射光的辐射强度IA， s和日光辐射强度Is、 散射角θ以及散射路径长度l的关系。 由于日光辐射强度为常数， 可知大气散射光的辐射强度仅与散射角以及散射路径长度相关， 即影响星点成像的地气光的辐射强度受散射角和散射路径长度的影响。

3基于地气光背景灰度模型的预处理算法

基于以上对地气光辐射强度特性的分析， 探究了地气光背景在星图中的分布规律， 进而构建了局部区域内的地气光背景灰度模型， 然后基于该模型设计了一种抗地气光的星图预处理算法， 如图5所示。

利用星图中某点的相邻像素的灰度值， 对局部范围内背景灰度模型的相关参数进行估计， 进而计算得到该点的背景灰度值。 再从原始星图中减去该灰度值， 以实现地气光背景的补偿， 得到预处理后星图。

3.1局部范围的背景灰度模型

天文导航中使用的导航星光高度通常高于20 km［16］， 相对应区域内大气散射光的散射路径长度l与传输系数T（l）的关系如图6所示。

在背景估计过程中， 取像素邻域的范围为10 pixel×10 pixel。 对于近地空间飞行器而言， 其飞行高度通常低于200 km， 在局部像素邻域范围内所接收到的地气光在大气中的散射路径长度变化幅度不超过300 km， 因此， 可用三次函数对图6中的传输系数进行分段拟合， 即

T（l）=k1l3+k2l2+k3l+k4（20）

式中： ki（i=1，  2，  3，  4）为模型系数。