云环境下一种联盟形成博弈的虚拟机迁移算法

摘要：虚拟化被认为是云数据中心实现计算资源多样化和系统管理高效化的关键技术。然而，虚拟机的不当放置方式导致了资源分配的不平衡。虚拟机迁移是一种帮助云服务提供商有效、自主地管理云资源的方法。虚拟机迁移问题被建模为联盟形成博弈（VMM-CFG算法） ，并提出了一种合并和拆分算法来实现虚拟机迁移。仿真结果表明，VMM-CFG算法在负载平衡方面表现良好。

关键词：虚拟机迁移;虚拟化;云计算;联盟形成;联盟博弈

中图分类号：TP301.6   文献标识码：A

文章编号：1009-3044（2022）20-0108-03

1 引言

云计算作为一种新兴的计算模型受到了广泛的关注和应用。服务供应商越来越愿意将服务从本地集群迁移到云数据中心。云数据中心将虚拟化技术作为实现计算资源多样化、促进系统管理高效化的关键技术。虚拟机通过虚拟化技术创建，被部署在物理机上。在云场景中，服务供应商请求资源，平台将任务请求部署到资源池的主机中。但是，云数据中心通常无法高效运行。效率低下主要是因为虚拟机的分配方式不合理，导致物理机资源负载不平衡，一些物理机过载，一些物理机无法充分利用[1]。虚拟机迁移算法是一种帮助云供应商提供有效、自主管理云资源的方法。虚拟机迁移使用迁移技术将负载从一台物理机转移到另一台物理机，以平衡物理机之间的负载，提高物理机利用效率。

在虚拟机迁移过程中要考虑两个关键问题。一方面，如何从高载物理机中选择出待迁移的虚拟机。云平台中，两个位于不同物理节点的虚拟机的通信成本比位于同一个物理节点的要高，因为数据通过内存传输比通过网络传输成本低。因此，无论是迁移还是保留高载物理机中的虚拟机，都应该考虑通信成本。另一方面，应该选择哪个低载物理机来放置待迁移的虚拟机。当有许多虚拟机需要迁移，并且有多个低载物理机满足迁移条件时，待迁移虚拟机和低载物理机的映射关系就要考虑。

虚拟机迁移算法很多，如装箱算法[2-3]、遗传算法[4-5]、蚁群优化算法[6]等。本文提出了一种基于联盟形成博弈的虚拟机迁移算法（简称VMM-CFG） 。联盟博弈是一个设计公平、稳健和高效协作策略的非常强大的理论[7]。联盟形成博弈是联盟博弈论的一个分支，与经典博弈和联盟图博弈不同，网络结构和合作成本在联盟形成博弈中起着重要作用。本文将虚拟机迁移问题建模为基于合并和拆分算法的联盟形成博弈。首先，从高载物理机中筛选出待迁移的虚拟机。接着，待迁移的虚拟机根据相应的约束自主形成联盟结构。待迁移的虚拟机可以通过不断执行合并和拆分操作来更新联盟结构，直到形成稳定的联盟结构。联盟结构中的每个联盟都映射到相应的低载物理机。最后，根据待迁移的虚拟机和低载物理机之间的映射，执行迁移。

2 问题模型

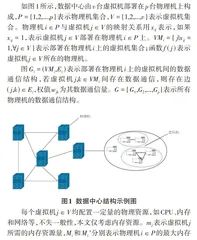
如图1所示，数据中心由[v]台虚拟机部署在[p]台物理机上构成，[P={1，2，...，p}]表示物理机集合，[V={1，2，...，v}]表示虚拟机集合。物理机[i∈P]与虚拟机[j∈V]的映射关系用[xij]表示，如果[xij=1]，表示虚拟机[j∈V]部署在物理机[i∈P]上。[VMi={j|xij=1，∀j∈V}]表示部署在物理机[i]上的虚拟机集合;函数[f（j）]表示虚拟机[j∈V]所在的物理机。

图[Gi=（VMi，Ei）]表示部署在物理机[i]上的虚拟机间的数据通信结构，若虚拟机[j，k∈VMi]间存在数据通信，则存在边[（j，k）∈Ei]，权值[wjk]为其数据通信量。[G={G1，G2，...，Gp}]表示所有物理机的数据通信结构。

每个虚拟机[j∈V]均配置一定量的物理资源，如CPU、内存和网络等，不失一般性，本文仅考虑内存资源。[mj]表示虚拟机[j]所需的内存资源量，[Mi]和[Mi′]分别表示物理机[i∈P]的最大内存容量和负载安全阈值，[mi]表示物理机[i∈P]实际的内存使用量，即：

[mi=j∈VMimj] （1）

若[Mi′<mi≤Mi]，则称物理机[i∈P]是高负载的;否则是低负载的。高载物理机集合表示为[H={i|Mi′<mi≤Mi，i∈P}]，低载物理机集合表示为[L={i|mi≤Mi′，i∈P}]。虚拟机迁移最主要的目标是最小化高载物理机数目[H]，实现负载均衡[1]。

3 基于联盟形成博弈的虚拟机迁移方法

考虑到动态迁移的实时性以及时间性能要求，本文研究设计一种基于联盟形成博弈的迁移方法，具体方法如图2所示。1） 制定选择规则，从高载物理机中筛选出待迁移的虚拟机;2） 待迁移虚拟机之间运用联盟形成博弈理论自主演化形成稳定的联盟，最终完成联盟与低载物理机间的映射，并实现迁移。

3.1 虚拟机选择算法

待迁移虚拟机选择算法目标有两个：1） 使高载物理机的实际资源使用量不高于负载安全阈值;2） 使通信紧密的虚拟机保留在原物理机，即将与其他虚拟机无通信或通信较少的虚拟机迁出。算法的具体描述见算法1。对于每个高载物理机[i∈H]，首先计算每个虚拟机[j∈VMi]的通信量[cj]，即与该物理机中其他虚拟机之间的数据通信量之和：

[cj=（j，k）∈Eiwjk] （2）

然后，根据通信量[cj]进行升序排列。如果序列中第一个虚拟机迁出，该物理机仍然高载，则将该虚拟机加入待迁移虚拟机集合[VMList]，继续判断下一个虚拟机，直到该物理机低载。依次遍历所有高载物理机。

[算法1  虚拟机选择算法 输入：[H，G]

输出：[VMList]

1. [VMList←∅]

2. for [i∈H] do

3.   for [j∈VMi] do

4.     [cj=（j，k）∈Eiwjk]

5.   end for

6.   [VMi′←{j|cj is sorted by an ascending sort}]

7.   for [j∈VMi′] do

8.     if [k∈VMi′＼{j}mk≥Mi′] then

9.       [VMList←VMList⋃{j}，VMi′←VMi′＼{j}]

10.     end if

11.   end for

12. end for ]

3.2 虚拟机联盟形成算法

筛选出待迁移的虚拟机集合后，要考虑如何将这些虚拟机迁移到低载物理机，即待迁移虚拟机与低载物理机间的二次映射问题，类似于装箱问题[2]和二次分配问题[8]，是NP难问题。在映射过程中，既要考虑物理机的内存容量，又要考虑网络通信成本。

本节运用联盟形成博弈理论，让待迁移虚拟机自主形成虚拟机群，整体映射到同一个低载物理机。下面给出一些定义：

定义1：待迁移虚拟机集合[VMList]的任意子集称为联盟[C⊆VMList]，若存在一个低载物理机[i∈L]，使得[j∈Cmj≤Mi′-mi]，则联盟[C]为有效联盟。[VMList]的一个划分称为联盟结构[∏={C1，C2，...Ch}]，满足[Cg⋂Cl=∅，∀g，l∈{1，2，...，h}，g≠l且k∈{1，2，...，h}Ck=VMList]。[Σ（Π）]表示所有可能的联盟结构。同样，若联盟结构[∏]内所有联盟均为有效联盟，则[Π]称为有效联盟结构。

定义2：给定联盟结构[Π∈Σ（Π）]，其值[v（Π）]定义为所有虚拟机之间总的通信成本，即：

[v（Π）=j∈Vk∈V，j≠kd（f（j），f（k））·wjk] （3）

[d（f（j），f（k））]表示物理机[f（j）]和[f（k）]的单位通信成本，如果[j]和[k]部署在同一个物理机，则[d（f（j），f（k））=0]。

定义3：给定联盟结构[Π]和[Π]，[∏]优于[∏]当且仅当[v（Π）<v（Π）]，记为[Π≻Π]。给定有效联盟结构[Π]以及两个集合[C1={j=1kCj}]和[C2={C1，C2，...，Ck}]，定义两种比较操作：合并[⊳m]和分割[⊳s]。

[[C2⊳mC1⇔v（Π＼C2⋃C1）≻v（Π）]

[C1⊳sC2⇔v（Π＼C1⋃C2）≻v（Π）]

[∀Ci，i=1，2，...，k]是有效联盟。 （4） ]

依据上述两种操作，联盟形成过程如下：首先，将每个待迁移虚拟机视为单一联盟，形成初始联盟结构。接着随机选择两个联盟并判断能否合并，若满足合并条件则合并，直到不存在任意两个联盟能合并为止。在某个低载物理机中的资源足以支持新联盟的条件下，新联盟被映射到相应的低载物理机中。映射过程由算法2中的MapProcess（·）执行。随后遍历任意联盟，判断是否存在其划分满足分割条件，若满足则进行分割，将分割的联盟分别映射到低载物理机。最后，迭代执行上述合并和分割过程，直到达到迭代次数或联盟结构无变化为止。算法的具体描述见算法2。

[算法2  待迁移虚拟机联盟形成算法 输入：[VMList]

输出：[Π]

1. [Π={{j}j∈VMList}]

2. repeat

//Merge Process

3.   repeat

4.     Select coalition [Ci，Cj∈Π] randomly

5.     MapProcess（[Ci⋃Cj]）

6.     if [Ci⋃Cj⊳m{Ci，Cj}] then

7.       [Ci←{Ci，Cj}，Cj←∅]

8.     end if

9.   until There are no two coalitions satisfying the merging condition

//Split Process

10.   for all [Ci∈Π] and [|Ci|>1] do

11.     for all the partitions [{Cj，Ck}] of [Ci] where both [Cj，Ck] are effective coalitions do

12.       MapProcess（[Cj]）， MapProcess（[Ck]）

13.       if[{Cj，Ck}⊳sCi]then

14.         [Ci←Cj，Π←Π⋃Ck]

15.       end if

16.     end for

17.   end for

18. until [Π] no change or loop number is reached ]