基于双曲线渐近线与TDOA的定位模型研究

摘要：针对传统双曲线定位模型求解计算较为复杂，低端微处理器无法满足实时定位运算需求的问题。该文对传统双曲线定位模型做出改进，研究了一种基于双曲线渐近线和TDOA的二维平面定位模型，并据此提出了一种三维空间目标定位的设计方案。利用Matlab软件分别对二维平面和三维空间的定位模型进行仿真验证，在STM32单片机上进行二者的运算速度对比，结果表明，该文所提出的定位模型在整体运算速度上要比传统模型快33%左右。

关键词：双曲线定位算法;TDOA;双曲线渐近线;三维空间目标定位

中图法分类号：TN802      文献标识码：A

文章编号：1009-3044（2022）25-0011-04

开放科学（资源服务） 标识码（OSID） ：

双曲线定位是传统导航手段当中一种简单易行的方法[1]，虽然随着科技的发展，各类定位技术涌现，如目前常见的质心定位法、三角定位法、航卫推算法、粒子群定位算法、神经网络定位算法等[2-4]，但由于传统双曲线模型原理简单，且易于实现，如今在航海、航空领域、室内定位仍广泛使用[5]。

定位的指标主要有两点：一是精度，二是实时性。在双曲线定位模型的基础上，对于精度的改良，许多学者都进行了大量的研究。文献[6]提出了利用双曲线定位和广义互相关法来提高定位精度，文献[7]提出了在室内定位中，可添加N个信标点，采用最大似然估计法来提高定位准确度，虽然提高了定位精度，但却给双曲线定位模型引入了新的计算因子，MCU处理器计算目标点坐标的时长增加，定位实时性下降。在目前高端芯片供不应求的情况下，低端处理器运算性能无法满足实时定位的运算需求，采用传统双曲线定位的系统在定位实时性上难以达到较好的效果。

为解决上述问题，本文以传统双曲线定位算法为基础，并加以改善，旨在研究出一个合适的新模型，并提出相对应的算法，简化双曲线定位模型的计算量，提高整体模型的计算效率，进而提高整体系统的定位实时性。

1 基本原理

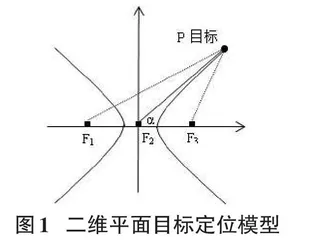
本文提出了一种基于TDOA与双曲线渐近线的二维平面目标定位模型，具体如下图1所示。图中P为目标，且处于第一象限，在同一直线上的F1、F2和F3处安置信号接收器，一般接收来自目标P所传递的声信号、光信号或电磁波等信号，设线段F1F2 = F2F3=d。

首先测得目标P到F1和F3的时间差为∆t1，P到F2和F3的时间差为∆t2，并且通过测量可知声信号、光信号或电磁波信号的传播速度为v，所以有关系式|PF1-PF3|= v∆t1，即目标P必在以F1和F3为焦点、F2为坐标原点、v∆t1为实轴长的双曲线上，列出双曲线的标准方程。

[x2a2-y2b2=1]              （1）

其中实轴长2a=v∆t1，焦点长2c=F1F3=2d，根据关系式a2+b2=c2可求出虚轴b，最终可求得渐近线与x轴的夹角[α=arctanba]。根据双曲线性质，若目标P距离F1和F3足够远时，目标所在的双曲线与其渐近线非常趋近，而在实际测量时，目标往往都离测量设备较远，此时可以认为目标P在渐近线上，即此时目标P与x轴的偏角等于渐近线与x轴的偏角，所以PF2与F2F3的夹角为：

[α=arctan（2d2-vΔt122vΔt1）]         （2）

式（2）中的d、v和∆t1皆为可测物理量，因此α可以由式（2）计算得出。

设目标P的坐标为（x，y），根据直角三角形的三边关系可得以下几个关系式：

[y=xtanα]             （3）

[PF22=x2+y2]               （4）

[PF32=x-d2+y2]          （5）

由所测目标P到F2和F3的时间差∆t2，可得到|PF2-PF3|=v∆t2，因此联立上面三式可得：

[x=-d2+vΔt22d+vΔt2tanα2+12vΔt22-2d2+2vΔt22tanα2]  （6）

[x=-d2+vΔt22d-vΔt2tanα2+12vΔt22-2d2+2vΔt22tanα2]  （7）

式（6）为P处于y轴右侧计算公式，式（7）为P处于y轴左侧的计算公式，即所求坐标结果有两个解，之后与传统双曲线定位模型处理过程一样，通过相位差、幅度差等方式，判断在双曲线的某条边上，进一步筛选出真实值。

在此基础上[8-10]，本文提出了一种三维空间目标定位模型的设计方案，如图2所示。图中P为目标，坐标为（x，y，z） ，首先在Z轴上依次安置三个信号接收器（F1、F2和F3） ，在Y轴的正半轴安置一个信号接收器（F4），其中F2为三维空间直角坐标系的坐标原点，设线段F1F2 = F2F3= F2F4=d，目标P到各接收器的距离分别为PF1、PF2、PF3、PF4。

首先测得目标P到F1和F3的时延差为∆t1，P到F1和F2的时延差为∆t2，P到F2和F4的时延差为∆t3，并且已知目标P所传递的光信号、声信号或电磁信号的传播速度为v。以三维空间直角坐标系的第一象限为例，若仰角和目标P到原点F2的距离确定，此时不管方位角为多少度，声源的z坐标都为定值，取声源与Z轴的截面图，如图3所示。

研究对比发现，此时的三维空间截面（图3） 与二维平面（图1） 一致，并满足二维平面目标定位模型的所有条件，若假定的目标P处于第一象限，因此利用二维平面目标定位模型推导出z的值如下：

[z=-d2+vΔt22d+vΔt2tanα2+12vΔt22-2d2+2vΔt22tanα2]  （8）

上式（8）中的参数d、v、∆t2和α皆为已知变量，因此可求得z，并根据三角关系求出[PF2=zcos（α）]。

在三维空间直角坐标系中，如图2所示，存在以下几个关系式：

[x2+y2+z2=PF22]           （9）

[x2+y-d2+z2=PF42]          （10）

[|PF2-PF4|=vΔt3]           （11）

联立以上三式可以求得：

[x=-d4+4（dPF2）2-4PF2Δt3vd2+2（dΔt3v）2-4（dz）2-4（PF2Δt3v）2+4PF2（Δt3v）3-（Δt3v）42d]

（12）

[y=d2-（Δt3v）2+2PF2Δt3v2d]          （13）

式（12）和式（13）中的参数d、PF2、∆t3、v和z都已知，因此可以根据二式，求出目标P的x坐标和y坐标，至此求出目标P在三维空间直角坐标系中的坐标（x，y，z） 。

2 定位模型的仿真验证与分析

本次实验在Matlab中进行，且为理想条件。为了验证上述模型，下文所述二维平面定位模型简称二维模型，三维空间定位模型简称三维模型，文中无单位标注的物理量，所用单位均为国际标准单位。

搭建如图1和图3所示模型，假设目标P为声源，在不考虑声音传播的衰减、混响、噪声等情况下，即声源P到各个信号接收器之间为理想传播，利用Matlab进行声源定位模型仿真，设置F1、F2、F3和F4之间间距d为0.02m，声速为340m/s。

2.1 定位模型验证

在二维平面目标定位中，如图1所示，因为实验条件是理想传播，即可认为，通过声源P到各个接收器之间的距离关系计算所得的理论值∆t1和∆t2，等于各个接收器最终检测所得的实际时间差数值（三维空间验证中同理） 。以第一象限为例，在其中选取一组二维平面中的随机点作为声源P的坐标，并记为实际坐标（x，y），将参数d、v、∆t1和∆t2带入式（3）和（6）中，计算所得坐标，记为公式坐标（x0，y0），并记坐标误差（x0-x，y0-y），验证后的结果整理至表1中，单位均为国际标准单位。

由表1可看出随着x的增大，理论上误差越来越小现象，并未出现，而造成这一现象的原因便是角度误差，不同的角度对应的坐标所产生的误差各不相同，后续会加以验证。

在三维空间中，如图2所示，验证过程与二维平面一致，以第一象限为例，选取一组随机点记为实际坐标（x，y，z），再将参数d、v、∆t1、∆t2和∆t3带入式（8）、（12）和（13）中，计算所得坐标，记为公式坐标（x0，y0，z0），并记坐标误差（x0-x，y0-y，z0-z），验证后的结果整理至表2中。

由表2可看出三维模型所产生的现象与二维模型相一致，原因在于前者是在后者基础上建立的，因此具备了由后者带来的误差，这一点从图3和式（8）、（12）和（13）可知。三维空间的误差主要是由于二维平面的误差造成的，因此下面对二维平面的误差产生原因做出验证。

2.2 误差分析

本文所提出的模型如图1所示，误差原因是利用了双曲线性质：当目标P距离F1和F3足够远时，目标所在的双曲线与其渐近线非常趋近。而上述理论中的趋近一词并不意味着相等，用渐近线与x轴的夹角（以下简称渐近线夹角），代替双曲线上的点和原点的连线与x轴的夹角（以下简称双曲线夹角），此过程中产生了理论误差。

记双曲线夹角为[α1]，渐近线夹角为[α2]，记角度误差∆[α]=[α2]-[α1]，由于[0≤α1≤90]，则以每10°分为一个小段，并从每个小段中随机选定一个角度作为[α1]的值，求出随着x的增大，对应的角度误差∆[α]，验证后的数据记录至图4中。

观察图4可知随着x的增大，不同[α1]下的∆[α]都呈下降趋势，满足随着距离的增大，双曲线和渐近线愈加趋近这一特性。从图4可知，不同角度下的∆[α]曲线在x为0.5～1.5m之间区别较大，而1.5m之后，各曲线之间的误差相对较小。为求出理论上的最大误差，在x=1m的条件下，[α1]处于0～90°之间，以1°为基本单位，对所有角度下的误差∆[α]进行对比，整理实验数据至图5中。

从图5中可以看出30°下存在最大误差，于是按前文定位模型验证中的方式计算对应的坐标误差，并记

[误差结果=x-x0x*100%]

y方向的误差结果计算方式与上式相同，经计算发现当实际值x为20米时，测量值的横坐标和纵坐标误差结果约为0.075%，当x为200米时，误差结果约为0.0075%，对于大多数定位场合而言，此时误差可忽略不计。

3 定位模型的计算速度对比实例

如文献[11]中所述，传统双曲线定位模型示意图如图6所示。

图中P为目标，在同一直线上的F1、F2和F3处安置信号接收器，一般接收来自目标P所传递的声信号、光信号或电磁波等信号，设线段F1F2 = F2F3=d。首先测得目标P到F1和F2的时间差为∆t1，P到F2和F3的时间差为∆t2，并且通过测量可知声信号、光信号或电磁信号的传播速度为v，那么令目标P的坐标为（x，y），则有方程组：

[vΔt1=x2+（y-d）2-x2+y2vΔt2=（x-d）2+y2-x2+y2]