剥开编程教学中“生活算法”的坚硬果壳

生活中的算法无处不在，如去医院要取号排队、调查问卷要分类筛选、家务劳动要统筹分治……生活中的算法也许与计算机的算法并不一致，但我们不能忽视信息科技对生活方式的革新，将生活中的思想方法与算法结合，对算法的学习也大有意义。

扑克中的“插入排序”算法思想

扑克中也蕴含着算法思想。在玩扑克时，通常要先洗牌，将牌打乱成无序状态，然后每个人轮流摸牌，为了方便出牌，每摸取一张牌，我们都会将其插入到手中已排好顺序的牌中，最终一堆无序的牌变成了我们每个人手中有序的牌，这是如何做到的呢？每摸一张牌，比手中的牌大就放后边，小就放前边；当手中的牌多起来，只需要将其插入到合适的位置即可，这就是插入排序算法的思想及其运用。

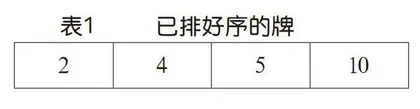
插入排序的过程

插入排序这的确是算法，程序设计中的插入排序跟玩扑克的排序方式是一模一样的，现在一起来回顾摸牌的过程，体验插入排序的原理：在开始抓牌之前，我们手中并没有牌，当摸取到第一张牌时，手中的牌就已经有了顺序。当摸取第二张牌时，一般习惯于按升序的方式来排列，如果这张牌比第一张小，就要放在前边，如果大就放在后边。例如，第一张是4，第二张是5，顺序就是4，5。第三张、第四张、第五张……以后的牌越来越多，要比较的次数就更多。假如你现在手中有4张排好序的牌（如表1），现在又摸了一张7，如何将这张牌插入到有序的序列中呢？我们可以将这张牌与最后一张比较，如果这张牌比10大，就直接放在10之后，如果小就与10之前的5比较，如果比5大就插到5之后（如表2）。

插入排序代码实现

在理解了插入排序思想并运用自如之后，代码就水到渠成了（如下页图1）。

可见，如果用生活中贴近计算机的算法案例让学生在玩中学、学中玩，往往会取得事半功倍的效果。

用“枚举”算法解密街头骗术

街上经常会见到一些摊位写着“不说话，猜你的姓氏，不准不要钱”“黄雀算命”等字样，这些看似输赢都是靠运气的游戏，吸引了不少人。下面笔者就以摸球游戏为例，探究这种街头游戏的秘密。

1.游戏规则

不透明箱子中有24颗小球（红色、黄色、蓝色各8颗），玩家每次抽取12颗小球，然后根据下页表3奖励金额情况，查看获奖金额。例如，抽到5个红球、7个黄球、0个篮球，就是750组合，奖励给玩家50元。

只有一种“543”的组合需要玩家付给摊主钱，其余都是奖励，一元钱可以玩5次，成本又很低，这就吸引了很多人参与游戏。

2.体验游戏

先尝试一次2元的，摸10次看看输赢情况。我们没有这套装备，可以用计算机程序来模拟一下这个过程，如下页图2所示。

用random随机数的方式模拟随机抽球的过程，a1，a2，a3表示每局游戏抽取三种颜色小球的数量，运行程序看看结果（如图3）。

程序运行两次，其计算结果如下。第一次：1+1+1-20+1+1+1+1-20+1=-32；第二次：1+1-20-20+1-20+1-20-20+1=-95。

3.解密原理

看到前面的游戏体验结果，发现两次游戏玩家都没有赚到钱，反而赔了不少钱，为什么呢？可以先思考如下两个问题：①24颗球抽取12颗有多少种组合情况？②为什么将543的组合设置为罚钱的组合，将840设置为最高奖励组合？先来回答第一个问题，按照程序中a1，a2，a3可能出现的结果，都在图2中有所体现，不过每种组合都可能包含6种情况，如543的组合包含了345，354，453，435，543，534这六种情况。再思考第二个问题，我们不妨大胆猜测是因为543组合出现的概率大，840组合出现的概率小。这是大多数人都能想到的猜测，那么它们的概率大概是多少呢？我们可以把这个解密原理的关键问题抽象出来，即转化为计算游戏中543和840出现的概率问题。

（1）探究问题。计算摸球游戏出现543组合的概率。

（2）算法分析。参考数学中计算抛一枚硬币正面朝上的概率，进行100次实验，统计正面朝上的次数，然后计算出正面朝上的频率。枚举n次实验，其中正面朝上的次数为r，则正面朝上的概率约为r/n，这里用到的就是枚举的算法思想。我们同样可以用这种算法估算出摸球游戏中543组合和840组合出现的概率。也就是枚举一定数量的实验结果，每次实验中统计出543或840组合出现的次数，具体算法流程描述如下：①设置枚举的样本总量n。②随机抽取12个小球。③统计小球的某种组合情况r。④重复第二步操作。⑤计算r/n的值。

（3）验证结果。对于a1，a2，a3是543的组合有6种情况如何判断呢？当然，枚举这6种情况是一种办法，但是条件会比较多，代码看起来会比较繁杂。另一种方法就是使用Python中的成员运算符“in”，只需要判断if（3 in [a1，a2，a3] and 4 in [a1，a2，a3] and 5 in [a1，a2，a3]）是否成立即可。当然，由于每次只抽取12颗球，a1+a2+a3的和为12是固定的，所以条件也可以优化为只判断两个数字即可，也就是if（3 in [a1，a2，a3] and 4 in [a1，a2，a3]），参考代码如图4所示。

运行程序记录结果如表4所示。

（4）得出结论。543组合出现的概率约是49%，也就是每两局游戏就可能会出现一次543，840出现的概率约是0.02%，从数学的角度去看原来摊主做的是稳赚不赔的买卖啊！