用长方形面积图来解决归总问题课堂教学探索

摘 要：本文的教学内容：过山车里的数学问题——平均速度。教学目标：1.经历几何模型的操作过程，进一步理解平均数的意义，掌握求平均速度的基本方法。2.通过独立思考与思辨式合作等学习方式，培养学生良好的思维习惯和数形结合能力。3.经历数学问题的抽象过程，体会数学与生活的密切联系。教学重点：掌握求平均速度的基本方法。教学难点：借助长方形模型理解平均速度问题，体验数形结合解决策略，感悟数形结合。教学准备：多媒体课件、预学单、课堂探究单、练习提升单。

关键词：数学教学; “平均速度”; 教学实录与思考

中图分类号：G623.5            文献标识码：A     文章编号：1006-3315（2019）9-085-002

一、情境引入，激发兴趣

师：今天我们一起学习过山车里的数学问题，学习前先看段视频

1.呈现过山车视频

师：看了这段视频，你觉得坐过山车让你记忆最深的是什么？

生：刺激。

师：这个刺激与我们数学中的什么问题有关？

生：速度。

2.引出学习内容

师：对！今天我们就来研究平均速度。

二、预学反馈，激化矛盾

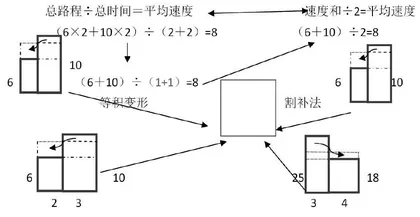
师：昨天老师让你们做了一份预学单，求：李明同学坐过山车，“上山”用了2秒，速度是6米/秒，“下山”也用了2秒，速度是10米/秒，他坐过山车的平均速度是多少米/秒？

师：发现大部分同学是这样列式的，出示预学结果：

你们是根据什么列式的？

生：总路程÷总时间=平均速度。

师：昨天老师请你们结合图说说你列式的想法，并在图中画出平均速度。

出示预学结果：

请同学上台说说找平均速度的理由。

生：左边长方形的长是2，宽是6，那么面积是12，这个面积就是上山的路程，左边长方形的长是2，宽是10，那么面积是20，这个面积就是下山的路程，这两个面积的和除以长（2+2）就是平均速度了。

师：平均速度在哪里？

生：指出

师：这时长方形应该成……

生：就是一个规则的长方形了

师：请你们再观察这2个图形，它们之间有什么联系？

生：面积不变，长不变，宽变了，这是利用等积变形。

2.出示预学成果，形成思辨材料

师：老师还发现另外一种计算平均速度的方法，出示（6+10）÷2=8米/秒，你们觉得这是根据什么列式的？

生：速度和÷2=平均速度。

师：你赞同这种算法吗？为什么？

生：赞同。（生）不赞同

师：我们来看这2个算式，你觉得它们之间有联系吗？

生：把第一个算式同时缩小2倍，就成第二个算式了：

（6×2+10×2）÷（2+2）=8

↓

（6+10）÷（1+1）=8

师：现在你觉得这个算法可行吗？

生：同意。

师：那么我们再来看图，他的想法你理解了吗？

生：我们可以把2秒时间同时缩小2倍，图形就

再利用割补法，它成

师：那么把时间同时扩大2倍回到原图，可行吗？

生：可行。

师：现在的平均速度在哪？

生：就是长方形的宽。

师：对，研究这1秒钟加1秒钟一组数据就能代表整体水平了。

实际速度和÷2=平均速度，就是总路程÷总时间=平均速度。

师：现在我们把2个不等宽长方形转化成一个长方形，面积不变，长不变，宽变了，解决了这个平均速度，那么以后我们求平均速度就用速度和÷2=平均速度好了。

生：行。（生）不行不行，时间不同应该不行。

师：到底行不行，接下来我们就应用长方形面积图来研究，拿出探究单。

【设计意图：借助长方形模型理解相同时间求平均速度的方法，进一步理解求平均速度的实际意义，并利用矛盾冲突，引出探究问题，激发探究兴趣。】

三、自主探究，构建模型

师：请学生拿出探究单：

出示探究要求：

1.请看清题意，独立思考;2.小组合作：（1）大胆说出自己的想法或疑惑;

（2）组员认真倾听并提出建议。3.展示汇报：

生：不能用速度和÷2=平均速度，只能用总路程÷总时间=平均速度，       因为大长方形上面多出来的面积按2：3分

配，2份割补到小长方形的上面，这样就成宽相等的长方形了。

师：不同时间求平均速度问题与相同时间求平均速度问题之间的联系与区别？

生：相同时间求平均速度2个数量关系式，不同时间求平均速度只能用总路程÷总时间=平均速度。

【设计意图：在不同时间求平均速度的操作过程中，进一步培养学生的数形结合能力。】

师：课堂小结：今天老师和你们一起利用2个大小不一的长方形图来解决求平均速度的问题，其实我们很多数学问题都可以用长方形图来解决。平均速度其实是个虚拟的速度是不存在的，但我们生活中有很多情况和求平均速度是一样的，接下来我们就利用长方形图来解决，请你们拿出练习拓展单，就用我们今天学的长方形面积的方法去做。

四、练习提升，深化建模

生：独立完成，用每千克25元的奶糖和每千克18元的水果糖，按奶糖3千克，水果糖4千克混合而成什锦糖。那么什锦糖每千克多少元？

生：用割补法在图中找到什锦糖的单价， 因为大长方形上面多出来的面积按3：4分配，4份割补到小长方形的上面，这样就成宽相等的长方形了。

【设计意图：进一步提升学生运用长方形模型解决相关的数学问题。】

五、全课总结

请同学们看黑板，这节课我们一起研究了什么内容？

生：研究了用2个大小不一的长方形面积来解决平均速度;生：利用了等积变形2个大小不一的长方形面积转化成一个宽相同的长方形，这个宽就是平均速度;生：……

师：是呀！今天我们利用了长方形面积图解决了平均速度问题，其实你只要利用好长方形面积这把利剑，你就能解决很多凝难数学问题。

【教学板书】

【教学反思】

本节上的内容不是经典的问题，是一个不起眼的问题，四年级学生平均数他们都会求，因此求平均速度自然是2个速度相加除以2了，而我们一般都给学生一个数量关系式让学生来解决这类题，可是发现用数来解决这个平均速度好像很抽象，而数学图形与数量关系之间的内在联系对学生来说是十分重要的。因此我就借助长方形面积模型理解平均速度问题，并延伸到求单价等问题来发展学生的思维。

一、经历过程，模块结构

思维的发展要有一个载体，选择了通过操作长方形的面积图来解决平均速度的问题，从而提高学生思维活动的自觉性，因为在课中学生有了在图中找到了相同时间的平均速度的经验，老师就相应的又让学生独立思考，再小组合作去研究，求不同时间过山车过A山的平均速度（用割补或其他的方法在图中找到平均速度），他们通过讨论，操作等手段，借助长方形模型理解相同时间求平均速度的方法，进一步理解求平均速度的实际意义，并利用矛盾冲突，引出探究问题，激发探究兴趣，积极主动地投入到学习中去。

二、重视应用，减少操练

思维要有可操作性，概括（合并同类项）是思维的基础，在教学中抓住概括能力的训练，是作为思维训练的基础，所以课堂练习的拓展求“用每千克25元的奶糖和每千克18元的水果糖，按奶糖3千克、水果糖4千克混合而成什锦糖。问：什锦糖每千克多少元？”借助长方形面积模型找到什锦糖的单价，进一步体验数形结合解决策略，感悟数形结合思想的重要性。

三、应用转化，丰富经验

思维的核心是概括，数学的本质是“类”与“模式”。本节课借助理解平均速度问题是总面积÷（总）长=（平均）宽长方形面积模型，从而让学生拓展到总价÷总数量=平均单价问题。

用长方形面积这把利剑促进学生思维的发展，让学生在小学数学这条道路上走的更顺更远。