聚焦思维提升的数学学习路径设计

促进学生思维发展是数学教学的核心任务之一。笔者以人教版数学四年级数学广角《鸡兔同笼》教学为例，阐述如何基于“课前预学、交流促学、适时导学、反馈展学”的学习路径展开教学，逐步提升学生的思维。

一、课前预学，激活思维

课前自主学习是激活学生思维的有效手段。笔者设计预学单作为学生课前自主学习的支架，激活学生的思维，引导他们生成多元的解决问题方法。

预学单分为“我的目标”和“我的研究”两部分内容。“我的目标”旨在明确预学任务和目标：研读教材第99页，了解“鸡兔同笼”问题；至少学会一种解决“鸡兔同笼”问题的方法。“我的研究”先给出问题情境“笼子里有若干只鸡和兔。从上面数，有8个头；从下面数，有26条腿。鸡和兔各有几只？”，然后提出以下两个问题。

问题1：你能尝试用下面两种方法解决问题吗？

方法1：画图

如果用1个圆圈表示1个头，我来画一画腿。（学生一般用表示兔）

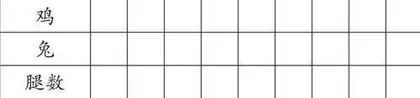
方法2：列表

问题2：你还有别的方法吗？把你的思路和结果记录下来。

课堂上，笔者展示部分学生的预学单，并让他们汇报自己的想法。一名学生说：“根据总腿数是26条以及鸡有2条腿，我画出13个头，但是题目告诉我们只有8个头，因此需要调整，而1只兔比1只鸡多2条腿，多出来5个头也就是多出来10条腿，把10条腿分别加在其中5个头下面，也就是把5只鸡变成5只兔，还剩下3只鸡。经过检验，5只兔和3只鸡正好是8个头和26条腿。”笔者点拨：“你把26条腿全部假设成鸡的腿，然后根据头数进行调整。你很会思考！”另一名学生说：“鸡和兔共8只，我先平均分，分别画4只鸡和4只兔，发现一共有24条腿，腿数少了2条，需要调整。把1只鸡变成1只兔就能增加2条腿，使腿数与题意相符，因此我的结论是笼子里有5只兔和3只鸡。”笔者点评：“你用平均分头数的方法解决问题，并通过鸡和兔的腿数关系很快找到了正确答案。”继而，有学生发现：如果笼子里的8只动物全部是兔，就有32条腿，而题目说明有26条腿，多了6条腿，把1只兔变成1只鸡就可减少2条腿，因此把3只兔变成鸡就能把多的6条腿减去，从而得到3只鸡和5只兔的正确答案。

学生利用数形结合的思想方法，从不同的角度思考，独立解决了问题，他们即使不能快速得出最优答案，也在推理过程中发展了数学思维。

二、交流促学，打通思路

思维发展是数学教学的核心。教师通过互动交流引发学生的共鸣、质疑、辩驳，有利于打通学生的思路，深化学生的认知，提高他们的逻辑思维能力和辩证思维能力。

学生汇报画图法后，笔者让他们交流列表法。一名学生说：“我采用的是一一列举的方法，假设笼子里全部是兔，就填0只鸡、8只兔，因为1只鸡有2条腿，1只兔有4条腿，所以共有32条腿，这与题意不符；接着调整为1只鸡、7只兔，计算出共有30条腿，这也不符合题意；再调整为2只鸡、6只兔……只有当鸡是3只、兔是5只时符合26条腿的条件。”笔者引导：“还有其他想法吗？”学生思考后提出不同的想法：“我发现增加1只鸡、减少1只兔，腿数就减少2条，于是我先填1只鸡、7只兔，共30条腿；为了减少腿数，我又填2只鸡、6只兔，共28条腿；继续减少腿数，填3只鸡、5只兔，就有26条腿，这与题目条件相符。”至此，学生的思维被打开。笔者抛出问题：“为什么这名同学没有继续往后写呢？”其他学生马上回答：“因为他已经找到了规律，继续往后写只会比26条腿少，不会再出现26条腿的情况。”笔者点拨：“也就是说，根据这种规律，不会出现第2种答案。看来列表时我们要边观察边思考，只要找到了规律，就可以更简便地解决问题。”此时，一名学生提出不同的想法：“我只列举了3种。如果鸡有1只，兔就有7只，总腿数是30条，不符合条件。于是，我一次调整到鸡有4只、兔有4只，此时总腿数是24条，这与26条相差2条。因为鸡变成兔可增加2条腿，所以我把鸡减少1只、兔增加1只，得出3只鸡和5只兔共有26条腿。”

学生通过交流体会到列表解决问题的灵活性，发现只要找到假设结果与题目条件之间的关系，就能根据规律快速得出正确答案。

三、适时导学，深化思维

数学教学要注重学思融合，教师要根据学情适时抛出关键任务或问题，给予学生尽可能多的表达想法、展示思路的机会，从而深化他们的思维。

为帮助学生实现从画图、列表解决问题到用假设法解决问题的过渡，笔者展示了用假设法解决问题的学生的预学单，并让学生分享解题思路。学生汇报：“假设笼子里全部是鸡，我用8个圆代表8只动物的头。1只鸡有2条腿，我在每个头下面画2条腿，一共画了16条腿，这与题目条件相比少了10条腿。于是我在鸡的头下面继续画腿，每只鸡下面要添2条腿，因为10÷2=5（只），所以要在5只鸡下面添腿，这样把5只鸡变成兔，兔就有5只，鸡就有3只。”在他的启发下，一名学生提出疑问：“继续在鸡的头下面画腿时，为什么每次画2条？”另一名学生解释：“因为假设全部是鸡，1只鸡有2条腿，而1只兔有4条腿，把1只鸡变成1只兔就要增加2条腿。”一名学生追问：“缺少的10条腿是怎么加的？可以讲得清楚一点吗？”笔者提醒学生利用学具在黑板上边演示边讲解。学生这样讲解：“先画鸡，即在每个头下面画2条腿，这时缺少10条腿。把1只鸡变成1只兔，就能增加2条腿。我们先加2条腿，把1只鸡变成1只兔。继续增加腿，我们可以发现，要加10条腿，就要把5只鸡变成5只兔。” 最后，笔者小结：“先假设8只都是鸡，算出总腿数，然后找到假设总腿数与题目中总腿数的差，最后通过1只鸡与1只兔的腿数差为2，即4-2=2（条），发现缺少的10条腿正好可以使假设的5只鸡变成5只兔，即10÷2=5（只），从而解决这个问题。我们把这种方法叫作‘假设法’。”

以上教学体现了以学生为主体，笔者适时引导学生以画图法为基础，用数学语言表达与交流，抽象出假设法解题的关键点，从而使假设法的理解和掌握水到渠成。

四、反馈展学，延伸思维

课堂尾声是学生思维提升的关键阶段，笔者在这一教学阶段着重引导学生建立知识点之间、学习方法之间的内在联系，促进学生思维延伸。

学生建立假设法的模型后，笔者引导：“回顾一下，画图法和假设法有没有相互联系的地方？”学生通过观察，发现假设法是在画图的基础上形成的。笔者指着板书抛出问题：“你能看出假设法和列表法之间有什么联系吗？”学生思考后提出：“当鸡是0只、兔是8只时，就是假设法的一种情况。”一名学生补充：“我发现表中兔最开始是0只，它由0只到5只的增加过程反映的就是假设法中的一个算式“10÷2=5（只）”，假设法中的算式“4-2=2（条）”反映的就是表中腿数的变化规律——每次减少2条腿。”

通过三种方法的勾连，学生不仅直观地找到了假设法与画图法、列表法的内在联系，还感悟到从特殊到一般的推理方式。

文字编辑  刘佳