依托“数学广角”渗透数学思想方法

人教版小学数学教材编排“数学广角”板块，旨在向学生渗透数学思想方法，发展他们的数学思维，帮助其逐步形成有序、严密思考问题的能力。本文以《搭配（二）》例3的教学为例，从单元整体教学视角阐述渗透数学思想方法的教学策略。

一、强化关联，关注整体

1.关注知识结构的整体性

数学教学要把握知识的生长点与延伸点，把每个课时的教学置于知识体系的整体建构中考量，处理好知识点与知识体系之间的关系，帮助学生建构结构化的知识。三年级《搭配（二）》是在二年级《搭配（一）》的基础上学习的，但问题中的数据加大了，问题情境更加复杂。因此，教师教学《搭配（二）》要带领学生回忆“搭配问题”的学习之旅，让他们体会到本节课知识是前面知识的延续，是“数学广角”知识整体架构的重要一环。

2.关注思想方法的一致性

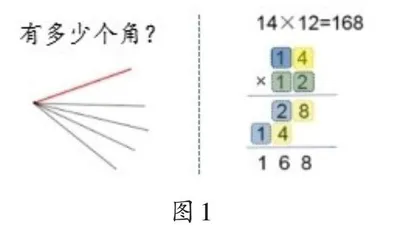
数学课程标准在教学建议中明确指出，教师“应揭示知识的数学实质及其体现的数学思想，帮助学生理清相关知识之间的区别和联系”。其实，之前的数学学习已经涉及“搭配问题”要着力渗透的有序思考的思想方法。教学例3时，教师可以适时出示图1，展示之前学习中遇到的数角的个数问题、两位数乘两位数笔算乘法计算过程等，启发学生思考这些内容中隐含着什么样的“搭配”，加深学生对不同知识所蕴含的相同数学思想方法的感知。

通过交流，学生感知到上述问题中蕴含的搭配技巧、有序思考的思想方法有助于问题解决。这些素材给学生提供了新的视角，让学生对前面学习的知识有了新的认识，重构了知识网络。

二、深度建构，关注过程

教学例3时，教师关注数学结果的形成和表达过程，通过精心设计的教学情境引导学生在已有知识基础上探索新的数学奥秘，通过多样化的教学方法和活动促进学生主动参与知识的构建过程，让数学知识不再是孤立的点，而是相互交织的知识网络。

从例3的教材内容来看，教师要重点聚焦问题情境的数学内涵，引导学生关注足球赛制，思考“每2个班级踢一场”的意思，这是学生正确理解题意、顺利解决问题的关键。课堂汇报时，有的学生认为“每2个班级踢一场”就是“2个班级踢一场比赛，不能3个班级一起比赛”，有的学生认为“每个班级都要和其他3个班级比赛一次”。在学生获得初步理解后，教师让学生用写一写、画一画的方式自主探究“一共要踢多少场”。由于学生已经学习了例1和例2，他们的记录形式多种多样，有用列举法记录每场比赛双方的，有连线表示比赛场次的。教师选择具有代表性的连线法组织全班学生交流。

学生的连线作品呈现出“方形”（如图2-1）和“直线型”（如图2-2）两种样态。<E：＼2020排版新＼教育教学＼2024＼12＼2024-12内文＼Image＼005.jpg>     图2-1                 图2-2

教师先让画出“方形”作品的学生复述连线过程。为放大学生的思维活动过程，学生演示连接从“1班”到“2班”的第一条线时，教师追问“这条线表示什么意思”，让大家体会一条线就代表一场比赛。然后，教师告诉学生：每连一条线就记一个数，边数边记录就能避免连完后数错的情况。在学生演示连接从“1班”到“3班”的第二条线时，教师追问“第2场比赛为什么还是从1班开始”，让大家在辨析中体会先安排好1班的所有比赛再安排其他比赛更有序。在学生演示从“2班”引出线时，教师追问“2班为什么没有和1班再连”，帮助大家形成2班再跟1班比就不满足“每2个班级踢一场”的规则，进而完善对足球赛制的理解。学生继续演示，最终连出6条线，得到共有6场比赛的结论。

“直线型”连线的结果如何呢？教师让学生在黑板上画一画、连一连，并说一说。在学生连出从“1班”引出的3条线并记录下比赛场次“3”时，教师引导大家关注2班，并追问：“从‘2班’出发连了几条线？要记录几场比赛？”有的学生认为从“2班”出发连了3条线，就应该记录3场比赛；有的学生认为3条线中有1条是从“1班”连出来的，重复了，因此只能记录2场比赛。通过辨析，学生的思考变得更加全面，并发现从“3班”出发的线只有1条，只记录1场比赛即可。最后，教师追问：“4班呢？比赛几场？记录几场？”有了前面的经验，学生清楚地知道“4班”分别与“1班、2班、3班”的连线所表示的3场比赛都是重复的，不用记录，进而总结出“3+2+1”的比赛场次计算规律，学会了在数形结合的基础上有序、全面地思考问题。

三、提升思维，强化思想方法

“数学广角”的教学有利于落实课程标准提出的“培养学生的抽象思维和推理能力”的目标。据此，教师教学例3时设计了有梯度的思维活动，助推学生在外化思维的过程中逐步提升抽象能力和推理能力，强化有序、全面思考问题的思想方法。

具象化思维活动。学习《搭配（二）》例1和例2后，学生已经掌握了列举、连线等解决问题的方法。在例3的教学中，教师首先让学生迁移运用列举、连线的方法分析与解决问题。

条理化思维活动。教师在分析学生作品环节用多个追问引导学生反思自己连线和记录比赛场次的过程和结果，从而改进连线方式，尝试有序连线，体会有序思考数学思想方法的价值。

推理性思维活动。在分析“直线型”连线环节，教师重点提出“参与了几场比赛”和“需要记录几场比赛”的问题，让学生感知其区别，明确记录的数据应该是要参与的比赛场次数，而不是聚焦一点看到的所有连线的条数，帮助他们进一步理解“每2个班级踢一场”的含义。课堂上，学生得出“1班记录3场，2班只用记录2场，3班只用记录1场，4班不用记录”的结论，实现了从具象分析到推理计算的思维提升，感悟到数形结合、有序思考的数学思想方法的妙处。

延展性思维活动。除了完成教材中的练习，教师还在课堂最后设计如下“为儿童节制作抽奖道具”作业，引导学生打破思维定式，把握解决问题的关键策略。

用红、黄、蓝、绿4种颜色制作抽奖道具。

①制作抽奖转盘。在以上4种颜色中选择2种，给图3涂色（每个区域只能涂1种颜色），有几种涂法？

②制作飞镖圆盘。在以上4种颜色中选择2种，给图4涂色（每个区域只能涂1种颜色），有几种涂法？

问题①的道具是转盘，左右区域颜色的交换对涂色结果没有影响。问题②的道具是掷飞镖的圆盘，2种颜色分别涂在内圈或外圈是有区别的。这两道题形成鲜明对比，有助于学生打破思维定式，把握“顺序对结果是否有影响”这个关键点，提高辨别与解决不同类型“搭配问题”的能力。

（作者单位：武汉经济技术开发区实验小学）

责任编辑  刘佳