对运算的一致性的理解及教学建议

【编者按】“数与运算”是“数与代数”领域的两大主题之一，是小学数学教学的重要组成部分。《义务教育数学课程标准（2022年版）》首次系统性地提出了“数与运算的一致性”，其中包含了数的概念的一致性与运算的一致性。帮助学生感悟运算的一致性，对于其运算能力、推理意识、符号意识等核心素养的发展有着重要意义。教师如何厘清运算的一致性的本质，以整体的视角观照数学教学，帮助学生实现核心素养的发展？本期话题围绕小学数学运算的一致性研究展开。

【摘 要】运算的一致性是《义务教育数学课程标准（2022年版）》对运算教学提出的新要求，其内涵主要表现为加法、减法、乘法、除法在整数、小数、分数运算中算理、算法的一致。落实好运算的一致性，需要厘清教学的要求，清晰其教学是一个循序渐进的过程；需要更系统、更到位地突出计数单位在运算教学中的实际作用和价值；需要结合小学生的实际直观表征算理和算法；需要从基础课和比较课两个层面把握关键课的教学；还需立足单元视角把握运算教学。

【关键词】运算 一致性 计数单位

运算的一致性是《义务教育数学课程标准（2022年版）》（以下简称《课程标准》）对运算教学提出的新要求。因此，在接下来的小学数学教材编写及教学中，突出运算的一致性应当成为运算教学的重要任务。作为一线数学教师，在基于《课程标准》编写的新教材还没有使用之前，正确理解运算的一致性，并在使用现行教材的过程中积极践行运算的一致性亦是非常重要的任务。

一、对运算的一致性的理解

运算的一致性，即加法、减法、乘法、除法在整数、小数、分数运算中算理、算法的一致。

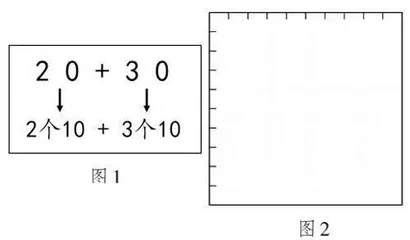
如20+30、0.2+0.3、[27]+[37]，这三个加法算式在运算时都会经历“2+3”（2+3的运算属于“基本事实”，是所有加减运算的基础）的过程。在现实背景中，这三个“2+3”的意义是不一样的，但如果将算式再抽象（算式本身就是抽象的结果）到运算更本质的算理与算法层面，就可以发现这四个加法算式之间的关系，能够感悟到加法运算本质上的一致性。20+30=2×10+3×10=（2+3）×10=5×10=50；0.2+0.3=2×0.1+3×0.1=（2+3）×0.1=5×0.1=0.5；[27]+[37]=2×[17]+3×[17]=（2+3）×[17]=5×[17]=[57]。在这里，10、0.1、[17]都是计数单位，2、3是计数单位上的数字（即计数单位的个数）。因此，加法运算的一致性就体现为：相同计数单位上的数字相加，计数单位不变。

减法是加法的逆运算，因此其运算的一致性又与加法一致。于是，加减法运算的一致性可以体现为：相同计数单位上的数字相加减，计数单位不变。

乘除法运算的一致性体现为：计数单位与计数单位相乘除，计数单位上的数字与计数单位上的数字相乘除。以乘法为例，0.2×0.3=（0.1×2）×（0.1×3）=（0.1×0.1）×（2×3）=0.01×6=0.06。其中“0.1×0.1”是计数单位与计数单位相乘产生新的计数单位，“2×3”（2×3也属于“基本事实”）是计数单位上的数字与计数单位上的数字相乘得出一共有几个新的计数单位。

二、对运算的一致性的教学建议

许多教师对运算的一致性的教学产生了困惑甚至质疑。比如，前文所述20+30的计算方法，用这样的方法教学20+30可行吗？当然不行！所以，关于运算的一致性，理解其内涵是一个方面，如何基于小学生的认知特点开展教学又是另一个方面。为此，笔者站在一线的视角，对运算的一致性提出如下教学建议。

（一）厘清教学要求

以“运算的一致性”作为关键词进行搜索，在《课程标准》中的相关表述一共出现了9次，分别出现在“课程目标”“课程内容”和“学业质量”部分中。仔细分析这9次描述，可以得到一些关于运算的一致性的教学要求。

1.运算的一致性的教学要循序渐进。

在《课程标准》关于运算的一致性的描述中，2次是在第二学段，6次是在第三学段。其中第二学段的关键词是“了解”，第三学段的关键词是“感悟”。

由此可见，运算的一致性的教学是一个循序渐进的过程，即在第二学段是了解——能借助具体实例进行说明；在第三学段是感悟——具有初步的理性认识。

之所以会有这样的循序渐进过程，一是与学生对数的认识是一个循序渐进的过程有关，二是与对运算的一致性的认识是在比较中实现的有关。

第一，对数的认识。学生对数的认识影响着他们对运算的认识。小学阶段学生对数与运算的认识分布大致如下表所示（以人教版为例）。

表1 小学阶段学生对数与运算的认识分布

[学段 年级 认识数 认识运算 要求 第一学段 一年级 100以内的数 整数加法、减法 100以内 二年级 万以内的数 整数乘法、除法 表内 第二学段 三年级 整数加法、减法 万以内 整数乘法 多位数乘一位数

两位数乘两位数 整数除法 除数是一位数 分数初步认识 分数加法、减法 同分母 小数初步认识 小数加法、减法 一位小数 四年级 万以上的数 整数乘法 三位数乘两位数 整数除法 除数是两位数 小数的意义 小数加法、减法 多位小数 第三学段 五年级 小数乘法、除法 分数的意义 分数加法、减法 异分母 六年级 分数乘法、除法 ]

从上表可以清晰看出，学生对运算的认识是从第二学段开始丰富起来的，这与一年级下册学习了“万以内的数”有着直接的关系。之后，在学习了分数之后，对应着逐步学习分数的加法、减法、乘法和除法，小数也是如此。

由此可见，学生对数的认识决定了学生对运算的认识，进而决定了学生对运算的一致性的了解与感悟。显然，这是一个循序渐进的过程，不可能一蹴而就。由此亦可明白，让学生感悟运算的一致性是一个长期的过程。《课程标准》指出，对数的认识不断加深，对数的运算的要求逐步提高，最后使学生感悟运算的一致性，便很好地佐证了上述观点。

第二，在比较中实现。一致，是没有分歧的意思，也可理解为是对于两个或两个以上的对象进行比较后的统一。这就是说，运算的一致性，不是在认识某一种运算时感悟到的，而是在学习了两种或两种以上的运算后进行比较而感悟到的。上表已经给我们启示，到第二学段学生对运算的认识开始丰富起来，此时对于运算进行比较的可行性开始显现，到第三学段随着学生对于运算的认识进一步丰富（包括学习了运算定律），进行比较的条件进一步充足，就能更好地让学生感悟运算的一致性了。

综上所述，强化运算的一致性的教学是整个运算教学的任务，不是某一种运算的任务，是一个长期坚持、循序渐进的过程。更进一步说，这里的一致性是对整个义务教育阶段的运算而言的，要使学生了解不同的数及四则运算之间的联系，感悟算理的一致性。

2.“感悟”是运算的一致性教学的最终目标。

在《课程标准》关于运算的一致性的描述中，有5次的行为动词是“感悟”，且都在第三学段。同时在“附录2：有关行为动词的分类”中对“感悟”的解释为：在数学活动中，通过独立思考或合作交流，获得初步的理性认识。也就是说，运算的一致性的教学，最终是要帮助学生对它的认识上升到理性层面，即要求教学要使学生从根本上去把握住运算的本质规律和内在联系，而不仅仅是停留在理解算理和得出算法层面。

（二）突出计数单位

通过对运算的一致性的内涵分析可以发现，感悟运算的一致性，核心是计数单位，即要突出计数单位在算理和算法中的意义。换言之，如果计数单位的教学不到位，那么就会给学生感悟运算的一致性带来一定的困难。

关于计数单位在运算中的意义，在我们当前的运算教学中是有体现的，但还不够系统和到位，这当然与之前没有强调运算的一致性有关。因此，在强调运算的一致性背景下，要在运算教学中更系统、更到位地突出计数单位的地位。

第一，更系统。更系统地突出计数单位，包含两个层面：一是在教学数的认识的时候更加突出计数单位的意义，使学生更好地理解整数、小数、分数都是由计数单位构建的；二是在认识运算的初期就开始突出计数单位在运算中的实际意义，让学生从一开始便在运算中感受到计数单位的作用，接触运算的本质规律。

第二，更到位。更到位地突出计数单位，即不是将计数单位作为理解算理和得出算法的桥梁，更不能过河就拆桥，而是要将计数单位作为运算的核心——体现本质规律和内在联系的关键。如将加法的运算方法在合适的时机提炼为相同计数单位上的数字相加，计数单位不变，便是更到位的体现。

（三）直观表征方式

20+30=2×10+3×10=（2+3）×10=5×10=50，显然不能用这样的方式教“20+30”。那么怎么办？其实我们以前也是这样教的，只是换了一种方式（如图1所示）。这样，就将“2×10”以“2个10”的方式表征，虽都是乘法分配律的意义，但后者显然更为直观，学生就能理解其中的道理。当然，为了学生能更好地理解，在得出“2个10”之前，一般还有10根1捆的小棒图作为过渡，逐步抽象。

在对运算的一致性的感悟中，涉及运算定律的运用，这对于尚未学习相关知识的学生而言，自然是一条走不通的路，因此需要改变表征方式。即使到了第三学段学生已经学习了运算定律，同样不建议直接采取运用运算定律再抽象后的形式化推理，而要引导学生经历探索直观表征的过程后再进行抽象。

如0.2×0.3，不能简单地将0.2×0.3看成（0.1×2）×（0.1×3），然后结合运算定律推理得出（0.1×0.1）×（2×3）=0.01×6=0.06，而是要引导学生探索其中的道理，借助几何直观进行表征。就如，为学生提供图2的学习工具进行探索、表征。通过画图，学生就能直观地看到0.1×0.1=0.01，产生了一个新的计数单位，2×3是在计算新的计数单位的个数，在此基础上再结合运算定律进行推理表达。

这样的探索过程不能忽视，更不能忽略。

（四）把握关键课例

在数学教学的过程中，不论哪个内容的知识，总有一些关键课。这些关键课中承载的知识教好了，后续的相关教学就会顺利。运算的一致性教学也是如此，比如在整数加减法教学中，一年级“两位数加减一位数”便是一节关键课，因为在这节课中首次涉及“数位对齐”，而“数位对齐”的本质便是“相同计数单位上的数字相加减”，这与加减法运算的一致性直接关联。

根据前文中关于运算的一致性的相关分析，与此相关的关键课大致可以分为两类。

第一类，关键基础课，即为后续感悟运算的一致性奠定知识基础的课。如上述一年级“两位数加减一位数”便是加减法中的关键基础课，因为在这节课中学生将比较正式地触及加法运算中的“计数单位”“相同计数单位上的数字相加减”等与运算的一致性紧密相关的知识。在乘法中，三年级“两位数乘两位数”也可理解为是一节关键基础课，因为在这节课中学生将首次遇到“计数单位与计数单位相乘产生新的计数单位”，这一知识将为学生后续进一步学习乘法和感悟乘法运算的一致性奠定基础。

第二类，关键比较课，即为了感悟运算的一致性而进行算理、算法比较的课。如三年级“分数的加减法”便是一节关键比较课，因为在理解了这节课中的算理和算法之后，便可将其与整数加减法进行比较，使学生初步了解加减运算的一致性。后续在学习了“小数的加减法”之后又可以进行比较，如此就可让学生感悟到加减法在整数、分数、小数运算中的一致性了。当然，比较也未必一定要在新授课中实施，也可以在复习中开展。到了六年级下学期总复习时，还可开展更为数学化的比较，帮助学生更好地感悟运算的一致性。

一般而言，开展一种新的运算教学时，或者是每一次数系扩充后的运算教学，可以理解为是运算的一致性的关键课。上好这些关键课，就可以帮助学生更好地感悟运算的一致性。

（五）立足单元视角