新课程背景下高中数学课时教学过程设计的探究与实践

［摘 要］新课程、新教材于2019年在五省（市）试点后逐渐在全国范围内铺开。文章重点探究新课程背景下高中数学课时教学过程的设计。首先，提出课时教学过程设计的界定及特征；其次，创造性地提炼出课时教学过程设计的四大原则；再次，依据课时教学过程设计的原则总结出课时教学过程“四环教学”模式；最后，依据课时教学过程设计原则对一节概念课做教学设计案例分析。

［关键词］新课程背景；高中数学；课时教学过程设计

［中图分类号］    G633.6        ［文献标识码］    A        ［文章编号］    1674-6058（2023）08-0013-04

新一轮的课程改革已经进入第四个年头，高中数学新课程提出单元教学理念和要求。单元教学体现了教学的整体性、主体性、发展性和境脉性，是发展学生学科核心素养的有效途径。在新课程背景下，教师应聚焦单元教学，有效实施课时教学设计。课时教学设计包含教学过程设计、教学目标设计、教学重难点设计、教学方法设计、教学环节设计等，本文主要研究课时教学过程设计。

一、课时教学过程设计的界定及特征

课时教学过程设计是指依据一定的教学理论、学习理论及传播理论，对一节课的教学内容进行精心设计、巧妙布局，形成一个操作性强、各环节紧密衔接的教学流程。课时教学过程设计应该具有科学性、创新性、整体性、衔接性和操作性等特征。

（一）科学性

课时教学过程设计的科学性体现在认真贯彻新课程理念及精神，符合学科教学的内在规律和学生的认知规律，同时保证传授知识的正确性，避免出现知识性错误。一个好的教学设计应依标合本，具有科学性。

（二）创新性

课时教学过程设计的创新性一般体现在两个方面：（1）教师能开创性地使用教材，教学设计灵活多样；（2）教师能广泛涉猎多种教学参考资料，充分利用各种教学资源，吸取同行的经验，结合个人的教学体会，巧妙构思、精心编排，设计出有别于他人的教学设计。

（三）整体性

课时教学过程设计的整体性体现在所传授知识的完整性和传授知识过程的完整性。知识的引入、发生、形成、表征及应用的教学要设计成一个有机整体，各个教学环节的设计也应该自然形成一个系统。

（四）衔接性

课时教学一般由若干个环节构成，虽然各个环节从形式上看是相互独立的，但同时又是有前后顺序的，因此，在设计课时教学过程时各环节之间要过渡自然、紧密衔接，避免相互脱节，影响教学的整体性和操作性。

（五）操作性

课时教学过程设计其实就是教师教学活动的“剧本”。教师依据课时教学过程设计开展课堂教学，落实教学目标，践行新课程理念，因此课时教学过程设计应具有较强的操作性。

二、课时教学过程设计的原则

经过多年的实践研究，笔者总结提炼出了高中数学课时教学过程设计的原则主要有知识的引入与发现、知识的形成与表征、知识的辨析与建构以及知识的应用与迁移。

（一）知识的引入与发现

新课程理念提倡让学生在了解知识的发现、产生、形成过程，这样学生才能更好地了解知识的来龙去脉，理解知识的内在本质；而引入是新知教学的第一步，也是新知识形成的基础，因此，在学习过程中，新知识的引入至关重要。当然，这里的引入教学不是为了“引入而引入”，应该杜绝那些照本宣科式的简单的引入课题的引入。教师应在引入教学中体现知识的产生、形成过程，引领学生发现新知识，并能带着愉悦的心情投入到新知识的学习中。

（二）知识的形成与表征

在通过“引入教学”让学生对新知识的产生、形成过程有了一定的认识后，教师引导学生进行互动交流，学生经过独立思考、自主探究、合作交流，了解知识的产生、形成过程，对知识有了一定的理解，但这并不等于学生就已经掌握了新知识，学生还必须能用某种形式将新知识表达出来，这就是表征学习。表征是认知心理学的核心概念之一，主要是指信息在人脑中记载和呈现的方式[[1]]。表征数学知识的方式，对于学生理解和应用数学知识至关重要。全美数学教师理事会编著的《美国学校数学教育的原则和标准》中指出“表征是数学学习的中心”[[2]]，这足以说明他们对数学知识的表征学习的重视程度。学生首先要会用文字语言描述新知识的内涵，其次要会用符号语言或图形语言表达新知识的外延，为应用新知识并形成新的基本技能打下坚实的基础。

（三）知识的辨析与建构

建构主义心理学认为，学生用自己的观点解读了教材的内容，从而在自己头脑中建构出一个新的概念，而且建构是和教学同步进行的，学生的学习是自己建构的过程，这种学习是探索性、研究性、理解性的学习过程[[3]]。知识所反映的对象来自客观世界，它不依赖人们的认识而存在，因此，知识也是客观性与主观性的对立统一。人们只有通过了解知识的产生、形成及发展过程才能感悟知识的内在本质，才能将知识接收于主观意识中，这就是知识的内化与建构过程。学生对新知识的内化需要通过知识的辨析教学来完成。辨析教学实际就是教师引导学生依据新知识的内涵与外延对一些具体的事例进行是非判断。辨析教学可让学生能够更加准确地理解和把握知识的本质，避免对知识的客观内容产生主观曲解，建构更加完整的知识体系，为知识的应用做好铺垫。

（四）知识的应用与迁移

学习的迁移是学习心理学中的概念，是指一种学习对另一种学习产生的影响[[4]]。任何学习都是在学习者已经具有的知识经验和认知结构、已获得的动作技能、习得的态度等基础上进行的，这种原有的知识结构对新的学习的影响就形成了知识的迁移，这是一种顺向迁移。知识迁移应该是双向的，即应用所获得的新知识、新技能解决问题的过程也是一种知识的迁移过程，叫作逆向迁移。学生掌握的学科知识都不是孤立、零散的，而是一个科学的、系统的整体，这个学习过程是漫长的日积月累的过程，需要不断增加知识量并将新的知识迁移同化到已有的知识体系中。

三、课时教学过程“四环教学”模式的建立

依据课时教学过程设计的四个原则，课时教学可分成与之相对应的四个教学环节，即新知导入教学、新知表征教学、新知辨析教学及新知应用教学，这一模式我们称为课时教学过程“四环教学”模式。

（一）新知导入教学

《普通高中数学课程标准（2017年版2020年修订）》指出：“高中数学教学以发展学生数学学科核心素养为导向，创设合适的教学情境，启发学生思考，引导学生把握数学内容的本质。”［5］ 基于这样的理念，教师应该主动创设真实、开放的数学教学情境，诱发、驱动学生主动参与新知识的学习。这里，数学教学情境指的是在数学教学过程中为了达到既定的教学目的，激发学生的学习热情，引发学生的情感体验，加强学生对新知识的感性认识而创设或营造的可以呈现数学教学内容的相应场景或氛围。常见的教学情境有生活情境、科学情境、文化情境和时事情境等。依据“知识的引入与发现”教学原则，教学情境还应该具有关联性、启迪性、可感性和目的性等特征，因此，我们称之为“导入式情境”。创设“导入式情境”不仅是为了引入新知和凸显教学目标，激发学生的学习兴趣和参与动机，更重要的是体现知识的发生、发展过程，让学生感悟到新知识从何而来、是如何形成的。

（二）新知表征教学

表征教学的目的是让学生应用简洁的数学语言准确地表述所学新知。首先，让学生自己组织文字语言表述新知；然后，教师给予反馈评价并给出准确规范的表述；最后，教师用适当的图形语言和符号语言对所学新知做进一步的表述，达到数与形的统一，便于学生对知识的应用，提升学生的数学素养。

（三）新知辨析教学

新知辨析一般分为正面辨析和反面辨析两类。首先是正面辨析，教师设计一组正面辨析题让学生依据所学新知进行判断，可以通过辨析新知的内涵得到肯定性结论；其次是反面辨析，教师可设计一组反面辨析题，其结论是否定的。当然，教师也可将两类辨析题合并呈现，让学生进行判断。

（四）新知应用教学

行为主义心理学认为，学习是学生头脑中某种联结的形成，通过反复练习形成某种技能。教师在教学时常先出示例题，然后由学生进行讨论，接着进行讲解，最后再让学生做练习。在很多情况下，经过反复的练习，不但能让学生形成某种技能，而且能巩固学生对新知识的理解与掌握，这种教学方法是教师经常强调和侧重应用的。依据这一教学原理，新知应用教学可按照“例题讲解→总结提炼→针对训练→反馈提升”的流程进行，但是教师在设计新知应用教学时应注意以下三点：一是定位要准确，要做好学情分析，依据学生的实际情况设置试题的难度、深度和广度，同时要依据教材的要求进行设计；二是针对性要强，主要以所学新知为背景设计题目；三是要有梯度性，题目设计除了要从易到难、从简单到复杂，还要由正用到逆用、由变用到综合应用。只有做到以上三点，才能达到学以致用、同化迁移的目的。

四、课时教学过程设计案例

按内容分类，新授课可以分为概念课、公式法则课和性质定理课三种课型。本文以“充分条件与必要条件”的概念课为例，对课时教学过程“四环教学”模式进行探讨。具体教学案例如下：

一、概念的引入与发现

（一）情境引入，回顾旧知

教师展示《相思》：红豆生南国，春来发几枝？愿君多采撷，此物最相思。提问：这是唐代诗人王维的诗《相思》，在这四句诗中，哪句可作为命题？

评析：从学生已有的知识经验出发提出问题，引导学生在“最近发展区”发现概念，符合学生的认知规律。从古诗文引入，体现学科融合，能有效激发学生的学习欲望，弘扬中华优秀传统文化，增强学生的文学素养。

（二）思考判断，发现新知

教师引导学生思考判断下列语句是否是命题，并判断真假。

（1）若平行四边形的对角线互相垂直，则这个平行四边形是菱形。

（2）若两个三角形的周长相等，则这两个三角形全等。

（3）若[x2-4x+3=0]，则[x=1]。

（4）若平面内两条直线[a]和[b]均垂直于直线[l]，则[a][∥][b]。

评析：从学生熟悉的命题出发，引入新的命题表述方式。在判断“若[p]，则[q]”形式的命题的真假的过程中，明确“命题的真假”与“由[p]推出[q]”的关系，顺利实现由“已有的知识结构”转入“新知建构”，从而发现“充分条件和必要条件”的形成过程。另外，充分条件和必要条件的学习涉及命题的真假，通过具体的例子有助于学生对这两个概念的理解。

二、概念的形成与表征

定义：如果“若[p]，则[q]”为真命题，我们就说：由[p]可以推出[q]，记作“[p⇒q]”，并且[p]是[q]的充分条件，[q]是[p]的必要条件。

如果“若[p]，则[q]”为假命题，我们就说：由[p]不能推出[q]，记作“[p⇏q]”，并且[p]不是[q]的充分条件，[q]不是[p]的必要条件。

评析：让学生能用文字语言与符号语言准确表述充分条件与必要条件的概念。

三、概念的辨析与建构

辨析题1：若小曹是台湾人，则小曹是中国人。

提问：这个命题的条件和结论分别是什么？命题是真是假？

结论：条件[p]“小曹是台湾人”是条件[q]“小曹是中国人”成立的充分非必要条件。

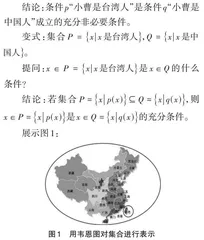
变式：集合[P=xx是台湾人]，[Q=xx是中] [国人]。

提问：[x∈P=xx是台湾人]是[x∈Q]的什么条件？

结论：若集合[P=xp（x）⊆Q=xq（x）]，则[x∈P=xp（x）]是[x∈Q=xq（x）]的充分条件。

展示图1：

总结：当两集合有子集关系时，小范围成立能推出大范围成立，即小范围成立是大范围成立的充分条件，大范围成立是小范围成立的必要条件。