核心素养下表现性目标的制订、实施与评价

［摘 要］以北师大版数学教材五年级上册“多边形的面积”单元为例，通过确定单元主题和核心素养、制订素养导向的单元目标、核心任务的设计与实施、单元整体的测评分析等环节，不仅有效落实了表现性目标的制订、实施与评价，为教师提供一个清晰的教学框架，还从“教—学—评”一致性的角度，激发学生学习的积极性和主动性，使学生了解自己的学习进度和不足之处，在数学学习上获得更好的发展。

［关键词］核心素养；“教—学—评”一致性；多边形；表现性目标

［中图分类号］ G623.5 ［文献标识码］ A ［文章编号］ 1007-9068（2025）03-0015-03

《义务教育数学课程标准（2022年版）》（以下简称“数学新课标”）以学科核心素养作为本学科的育人目标，倡导“教—学—评”一致性。这里的“教—学—评”一致性，指以清晰的目标为基础，教师的教学、学生的学习和对学习的评价是一致的。可见，清晰的目标是“教—学—评”一致性的前提和灵魂。下面以北师大版数学教材五年级上册“多边形的面积”单元为例，谈谈如何基于核心素养进行表现性目标的制订、实施与评价，实现“教—学—评”一致性。

一、确定单元主题和核心素养

北师大版数学教材五年级上册第四单元“多边形的面积”，属于第三学段图形与几何领域中“图形的认识与测量”的内容，对应的核心素养有量感、空间观念和推理意识等。这节课的教学目标是让学生运用割补、倍拼和分割等方法，将新图形转化为已学过的图形，从而计算出新图形的面积。

二、制订素养导向的单元目标

以素养为导向的单元目标，包括对单元内容的结构化分析、数学知识和基本素养内涵的确立，以及核心目标和具体表现的确定等。在进行单元内容结构化分析时，教师要将单元内容与前后知识联系起来；在确立数学知识和基本素养内涵时，教师要将单元知识与核心素养、关键能力的主要表现联系起来；在确定核心目标与具体表现时，教师要参考数学新课标中本单元的“学段目标”“内容要求”“学业要求”等，并比较不同版本教材的单元目标。

1.单元内容结构化分析

“多边形的面积”单元有比较图形的面积，认识底和高，探索平行四边形、三角形和梯形的面积，解决有关面积计算的实际问题等内容。“比较图形的面积”的教学，意在引出数方格的直观方法，为探索图形的面积积累经验。考虑到底和高在平行四边形、三角形与梯形的面积计算中的重要作用，“认识底和高”单独设为一课，为后续探索特殊的平面图形的面积奠定基础。探索平行四边形、三角形和梯形的面积是在学生掌握了图形特征与长方形、正方形面积的基础上学习的，其中平行四边形的面积是研究其他图形面积的基础。通过这些内容的学习，学生既可以运用变换思想推导出图形面积的计算公式，积累数学活动经验，又可以在探索组合图形面积等活动中发展空间观念，为进一步了解圆的面积和立体图形的表面积打下基础。

2.数学知识与核心素养内涵

“多边形的面积”单元对应的核心素养有推理意识，具体表现是能够运用化归的方法形成局部的演绎推理。如用格子图探索平行四边形的面积时，学生知道如何处理不是整格的情况，能利用数正方形和割补成长方形等方法求出平行四边形的面积；探索三角形的面积时，学生发现运用割补法不能直接得到三角形的面积，需要用倍拼法把两个完全一样的三角形转化成平行四边形；探索梯形的面积时，学生尝试把梯形转化成已学过的长方形、平行四边形或三角形。

3.核心目标与具体表现

对“多边形的面积”单元，数学新课标提出的“学段目标”是学习计算几何图形面积的方法，培养量感、空间观念和几何直观；“内容要求”是学习和掌握平行四边形、三角形与梯形面积的计算公式，进一步培养量感、空间观念和几何直观；“学业要求”是能够计算平行四边形、三角形和梯形的面积，并使用相应的面积公式解决实际问题；“教学提示”是帮助学生运用转化的思想推导平行四边形、三角形、梯形等平面图形的面积公式，培养空间观念和推理意识。

4.比较不同版本教材的单元目标

在比较北师大版数学教材和人教版数学教材中的“多边形的面积”单元目标后，确定本单元的核心目标是探索和掌握多边形面积的计算方法，将新图形转化为已学过的平面图形并计算其面积。核心目标具体表现在以下两个方面：一是具有转化意识，即学生先尝试通过割补法把平行四边形转化为长方形，再根据长方形的面积推算出平行四边形的面积；二是掌握转化方法，即学生发现用割补法不能计算出三角形的面积，所以先尝试用倍拼法将两个完全一样的梯形拼成一个平行四边形，利用梯形的面积是平行四边形面积的一半来推算梯形的面积，再通过梯形上底的动态变化，思考当上底是0时梯形就变成了三角形，由此得到三角形的面积。

三、核心任务的设计与实施

核心任务的设计与实施，包括单元学习路径分析、单元内容教学安排、核心目标制订等。

1.单元学习路径分析

为了更好地了解学生的学习起点，教师要设计开放性的前测题，真实地了解学生的思考过程。前测题的设计要基于单元核心目标，重点了解学生已经具备了哪些知识、方法和生活经验，特别要关注学生存在哪些疑惑，以此来分析学生达成单元核心目标需要经历的学习路径。

本单元教学，从转化意识和转化方法这两个角度对本班56位学生进行前测。通过前测，将学生的表现分成四个水平层次：水平0，8.9%的学生不会转化；水平1，32.1%的学生能把方格中的图形转化为平行四边形；水平2，26.8%的学生能把方格中的图形转化为三角形和长方形等，并做到转化前后图形面积不变；水平3；32.2%的学生至少能用2种方法计算出三角形的面积。

基于以上分析，对“多边形的面积”单元的学习路径做了相应的调整与优化：一是探索平行四边形的面积时，引导学生回忆已经学过的图形的面积计算，有目的地把新图形转化成会求面积的图形；二是探索梯形和三角形的面积时，引导学生思考并总结出将新图形转化成会求面积的图形有哪些方法，并比较这些方法之间的异同。

2.单元内容教学安排

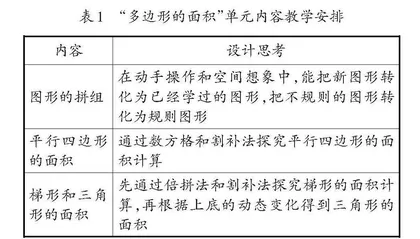
单元内容安排必须遵循两个原则：一是不能完全按照课本例题来安排，而应该按照核心目标中的核心任务来安排；二是要根据学情和学生的个体差异做适当调整。“多边形的面积”单元内容教学的具体安排见表1：

3.核心目标及核心任务的设计与实施

根据具体的表现性目标和学习路径，就可以在核心目标的统领下设计每节课的核心任务，并充分考虑教学活动的实施。核心任务的设计应结合核心目标的具体表现来设计，任务要与具体表现相对应；在设置学习任务时，要充分考虑教学活动的实施，根据不同的任务与对象预设学习方式、反馈方式和评价方式，确保“教—学—评”一致性。“多边形的面积”单元的学习目标和学习任务设计见表2：

四、单元整体的测评分析

单元整体备课的测评分析，包括后测题设计与后测题分析。后测题的设计指向单元核心目标的达成，分析可以从定性和定量两个维度进行，为诊断和改进教学提供依据。

教学“多边形的面积”单元后，通过后测题，对学生进行了后测，并将学生的后测表现分成四个水平层次：水平0，不会转化；水平1，5.4%的学生能把新图形转变成已学图形，即能把新图形转化为平行四边形；水平2，23.2%的学生掌握一种转化方法；水平3，71.4%的学生掌握不同的转化策略，即至少能用2种方法计算新图形的面积。

“教—学—评”一致性视角下的素养评价方式，既为教师提供了一个清晰的教学框架，从最终的教学目标出发来设计整个教学过程，又强调了“以评促学”和“以评促教”的原则，有利于教师及时发现教学中存在的问题，进而调整教学策略，极大地促进了学生的深入学习和教师的专业发展。通过确定单元主题和核心素养、制订素养导向的单元目标、核心任务的设计与实施和单元整体的测评分析等环节，将核心素养下表现性目标的制订、实施与评价在课堂中落地，有助于学生通过评价了解自己的学习进度和不足之处，在数学学习上获得更好的发展。

［ 参 考 文 献 ］

[1] 刘元跃.小学生逆向思维能力培养的探究：以“多边形的面积”教学为例[J].小学教学参考，2024（8）：52-54，58.

[2] 陈巧娟.统整理念下小学数学单元作业设计的思考与实践：以“多边形的面积”单元为例[J].小学数学教育，2024（9）：16-17.

[3] 李佳，李国良.一题一课，让思维深度发展：基于多边形面积单元拓展课“等积变形”的实践研究[J].小学教学研究，2024（11）：9-11.

（责编 杜 华）