以“精准活实”教学促“减负增效”学数学

【摘 要】“精准活实”教学是通过教师“四精（精打细算、精挑细选、精耕细作、精益求精）”、学生“两主（积极主动学、自主选择学）”，取得“两活（学习方法活、思维创新活）两实（学业基础实、素养提升实）”教学成效。以“精准活实”教学法对2002年高考数学压轴“剪拼题”进行探究教学，有助于激发学生的学习兴趣和学习动力，促进学生深度学习，培养学生实践能力和解决问题的能力，实现“减负增效学数学”。

【关键词】精准活实；减负增效；创新实践；教学感悟

【中图分类号】G633.6  【文献标志码】A  【文章编号】1005-6009（2023）16-0068-07

【作者简介】董裕华，江苏省海安高级中学（江苏海安，226600）校长，正高级教师，江苏省数学特级教师。

江苏省海安高级中学通过教师“四精”、学生“两主”，取得“两活两实”教学成效，形成“精准活实”教学特色，受到社会关注。2002年高考数学压轴“剪拼题”历久弥新，至今仍切合新课改理念。现笔者以该题教学实践为例，探究如何通过“精准活实”教学，激发知识迁移、激活脉络关联、激励主动创造，促进学生深度学习，更好体现学科育人价值，实现学科减负增效。

2002年全国I卷文科第22题：

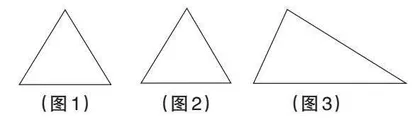
（1）给出两块面积相同的正三角形纸片（如图1、图2），要求用其中一块剪拼成一个正三棱锥模型，另一块剪拼成一个正三棱柱模型，使它们的全面积都与原三角形的面积相等，请设计一种剪拼方法，分别用虚线标示在图1、图2中，并作简要说明； （4分+4分）

（2）试比较你剪拼的正三棱锥与正三棱柱的体积的大小； （4分）

（3）如果给出的是一块任意三角形的纸片（如图3），要求剪拼成一个直三棱柱模型，使它的全面积与给出的三角形的面积相等，请设计一种剪拼方法，用虚线标示在图3中，并作简要说明。（本小题为附加题，如果解答正确，加4分，但全卷总分不超过150分）

这道题是整卷的压轴题，受答卷时间和心理压力的影响，有些考生未能发挥正常水平。但满分16分的试题，全国均分只有2.48分，着实让人匪夷所思。对于第（1）问，只要取三角形三条中位线（如图4），就可以折成正四面体（如图5），4分不难取得。学生感觉题目新、没想到、不适应，而权威部门对本题褒奖有加，认为它具有探索性，蕴含创意、精彩独特，是为数不多的“对于培养考生的实践能力和创新意识有重要的意义”的好题，它不仅考查学生的空间想象、动手（拼图）能力和类比、迁移的思想方法，还着重考查学生的创新能力，体现了“创设问题、提出问题→操作实验、探索规律→应用、解决问题”的研究性学习方式，有利于培养学生的空间想象能力，充分发挥其主观能动性和创造性。［1］

笔者多次尝试让高一新生完成这道题的第（1）（3）两问，学生给笔者很多惊喜，也让笔者思考：我们的课堂到底应该怎样培养学生的空间想象力、动手操作力、探究创造力？这既是老问题，也是常抓常新的问题。

一、“精准活实教学”的意蕴

“精准活实”是江苏省海安高级中学在长期的教学实践中形成的教学特色。我们始终把“怎样用尽可能‘少’带来尽可能多的‘好’”作为研究主题，“减负增效学数学”既是我们的主攻目标，也是我们的实践成果。

教师“四精”和学生“两主”，是“精准活实”教学的重要特征，其成果体现在学生的“两活两实”。

1.教师 “四精”

（1）精打细算。精心设计教学内容和环节，力求“教—学—评”一致；要求学生完成的练习，教师先试水、筛选，力戒错题、废题、无效题。

（2）精挑细选。充分挖掘优秀教学素材的生长、扩展和联通功能，由题及类、触类旁通、举一反三，发展学生观察、想象、探索和实践能力。

（3）精耕细作。通过对课堂和作业生态的实时监测和数据分析，既节省教师的时间和精力，又能及时发现学生的薄弱环节，提高教育教学的针对性和有效性。

（4）精益求精。准确把握学习起点，灵活取舍教学内容，突出整体驾驭和精讲精练，突出学科素养和能力提升，将因材施教落到实处。“准”以“精”为条件，“精”以“准”为标志，“精”“准”紧密相连，是教学减负增效的基础。

2.学生“两主”

（1）积极主动学。课堂上，90%以上的学生积极参与教学全过程，所学内容90%以上能被学生掌握。每节课的这两个“90%”，就能保证90%以上的学生取得理想成绩。尽管这三个“90%”只是教学质量评价的部分指标，但好的教学效果是对课堂教学的基本要求。

（2）自主选择学。学会选择是精准教学的基础。教师要帮助学生弄清自己有什么、要什么，再考虑给什么、怎么给，这是学生自主选择的保障。学生要学会权衡取舍，把主要精力集中在“跳一跳够得着”的有典型意义的问题上。

3.学生的“两活两实”

减负增效的成效主要体现在学生的“两活两实”。

（1）学习方法活。死记硬背和机械刷题容易使思想僵化。学生自主预习、钻研、归纳总结，自主模拟命题，制订评分细则，在“不经意间”也能达成教学目标，甚至超出预期。

（2）思维创新活。数学的本质是思维，思维又是创新的基础。培养思维能力是数学教学的重要任务。对学生而言，无论是问题还是结论，只要是他们发现的，都属于创新成果。要让学法活起来，让思维活起来，就要让数学真正用起来。“活”是“用”的目的，只有“用”才能“活”。

（3）学业基础实。没有扎实的基础，就难以形成核心竞争力。高考的80%题目考查基础，难题只有20%。但多数学生在占80%的基础内容上只用了20%的时间，却把80%的时间用在20%的难题上，不但做了许多无用功，连本来能得的分数也丢了不少，得不偿失。

（4）素养提升实。鼓励学生有效整合学科知识，运用学科方法，高质量地认识、分析、解决真实情境中的问题，提升能力素养，以适应当前和今后发展的客观要求。

二、“一道初中生能解的高考数学难题”教学过程［2］

1.激发知识迁移，完成基础剪拼

教师告知学生正三棱锥和正三棱柱的剪拼要求：正三棱锥由一个正三角形和三个全等的、底边长等于正三角形的边长等腰三角形构成（如图6）；正三棱柱由两个全等的正三角形和三个全等的、一边长等于正三角形边长的矩形构成（如图7）。

学生从小就进行过“折剪拼”的训练，绝大多数人拼出如图4、5的正三棱锥，也有不少人将剪拼正三棱锥的方法迁移到正三棱柱（如图8），先沿三角形中位线剪出1和2两个正三角形，将剩下的平行四边形变成矩形（三角形3移到4的位置），再将矩形分成3个全等的小矩形即可；或者如图9，先剪出正三角形1，再剪出矩形，剩下的两个直角三角形2和3拼成和正三角形1全等的三角形。大多数考生是可以做出第（1）问的。

2.激活脉络关联，拓展思维空间

教师引导：以前，我们怎样把矩形剪拼成无盖的长方体？

学生：只要在四个角都剪去同样大小的正方形，就可以达成目标。（如图10）

教师：怎样剪拼成有盖的长方体呢？

学生苦思冥想仍不得法。

教师提醒：正三棱柱是怎么剪拼的？能不能参照它的方法？

有学生想到先对折矩形，剪出两个正方形做底面，剩下部分再对折成四个侧面（如图11），就可以做成有盖的长方体。

教师追问：你是怎么想到的？

学生：正方形的四条边都相等，做侧面就比较方便，跟剪拼正三棱柱差不多。

教师用模型示意：把无盖的正三棱柱盒子剪开，平放到桌面上，能不能想象出它的形状？

学生很快画出图12，也知道这个形状由一个正三角形和三个全等的矩形构成。

教师又追问：这个“秃头秃脑”的形状，似乎缺了三个“角”，谁来补上？

学生自然想到了图13。

教师继续追问：图13中，阴影部分小三角形的顶点在大三角形的什么位置？

学生讨论后形成一致意见：尽管正三角形的三条高、三条中线、三条角平分线重合，但这里用到的只是角平分线，因为这里的小三角形顶点到大三角形两边的距离都相等。学生作出如图14的示意图，O点是作为△ABC的内心。

教师再追问：刚刚补上的三个角能不能拼成盒子的盖子？

学生讨论后发现，在图14中，从O点作△DEF三边的垂线，只要补上的三个“角”凑起来与△DEF重合，也就是D，E，F分别处在OA，OB，OC的中点时就能满足要求。

顺着这个思路，把一般三角形剪拼成直三棱柱就易如反掌。（如图15）

弄清整个剪拼的来龙去脉，把握关键点，第（3）问也不是高不可攀。

3.激励主动创造，提升能力素养

教师引导：将一般三角形剪拼成直三棱柱，还有其他方法吗？

受图8—图11的影响，学生通过作中位线，得到两个全等三角形1、2和一个平行四边形3。如图16的难点是把平行四边形3剪拼成一边长等于三角形1周长的矩形。

在教师的鼓励下，学生继续探究发现：如图17，在 ABCD中，如果AF（＜AC）的长度等于规定长度，将图中区域1移到2的位置， ABEF就满足要求。如果AC的长度还不符合规定，将 ABEF继续剪拼，经过有限次操作，总能让其边长达标。再用图8中三角形3移到4的方法，将平行四边形变成矩形。

教师引导：刚才，大家发现了一个重要结论：任何平行四边形，都可以剪拼成一边长符合规定的矩形。那么，一般三角形能否剪拼成一边长等于规定长度的平行四边形呢？

学生：同样利用中位线，把图18中的区域1移到2，区域3移到4，原来的三角形变成了矩形，再用图17的方法就行了。

教师：如果我们规定的边长比AB和AD都小，又怎么办呢？

学生：经过AD中点和BC中点作直线，将 ABCD一分为二。再将其上部拆移到下部的右侧。

教师：如果还不符合要求呢？

学生：重复刚才的做法直到满足条件。

教师继续引导：如果把三角形换成多边形，也能变成一边长等于规定长度的矩形吗？

学生豁然开朗：通过对角线将多边形分割成三角形，就可以按照上述方法，将每个三角形都变成规定长度的矩形，如图19，将区域1、2、3分别变成区域4、5、6，就能实现目标。

教师激励：刚刚，我们经历了一个伟大发现的过程——任何两个面积相等的多边形都可以通过有限次割补让它们全等。1833年，匈牙利数学家波尔约证明了这个结论，这个结论也称为波尔约-格维也纳定理。那么，这个结论能不能再推广到空间，怎么表述呢？

学生：任何两个体积相等的多面体都可以通过有限次割补的方法让它们全等。

教师：非常好！你们已经和大数学家具有同样的思维，真不简单！这种类比和猜想是创新思维的基础。1900年，德国数学家希尔伯特在巴黎国际数学家代表会上提出了23个数学问题，其中的第3个就是它。只不过直觉告诉希尔伯特，这个结果不一定正确。也就是说：两个体积相等的多面体不一定能通过割补的方法让它们全等。这个结论提出的当年，希尔伯特的学生就给出了证明。由此看来，直觉类比不一定可靠，还得经过严格的证明，否则还只是一个猜想。

有学生意外发现和图11差不多的思路：如图20，先把一般三角形变成矩形，再将矩形分割出两个正三角形，剩下部分三等分，就可以做成正三棱柱。

教师再激励：真没想到，你们不仅将一般三角形剪拼成直三棱柱，还直接拼成了正三棱柱，同学们真不简单！我们再思考一个问题。刚才，大家抓住特殊点、特殊线，让问题变简便。如果不用中点、中位线，这个问题还能不能解决呢？不妨设正三角形的边长为2，剪出的小三角形边长为x（x<1），如图21、22，又怎么做呢？