融合信息技术的高中物理创新微课程设计

摘   要：以“运动的合成与分解”章节中的“绳”模型速度关联问题为例，基于SOLO分类理论设计了多维素养递进式微课程，并进行了实践。探讨在TPACK视角下融合信息技术的高中物理创新教学及评价方式，以期更有效地落实物理学科核心素养的培养。

关键词：高中物理；创新微课程；信息技术；速度关联；TPACK

中图分类号：G633.7 文献标识码：A     文章编号：1003-6148（2024）10-0084-3

收稿日期：2024-04-15

基金项目：广东省中小学教师信息技术应用能力提升工程2.0专项科研课题“在中学物理创新课程中融合信息技术的实践研究”（TSGCKT2023102）。

作者简介：陈宏林（1986-），男，中学高级教师，主要从事中学物理信息化教学研究。

《普通高中物理课程标准（2017年版）》明确指出，高中物理教材应有效地利用信息技术［1］。这包括通过信息技术平台获取课程资源、利用信息技术进行互动交流以及使用信息技术工具进行辅助教学等方面。目前，在国内的中学物理教学中，信息技术的应用主要是以辅助教学为主。例如，在课堂教学中使用PPT或动画演示，或者在物理实验中使用数字采集器等。缺少对信息技术的深度融合，不利于提升学生的信息素养和物理核心素养。本文以“运动的合成与分解”中有约束的“绳”速度关联问题为例，基于TPACK和SOLO理论设计了一套深度融合信息技术的物理创新微课程。

1    TPACK及SOLO理论简介

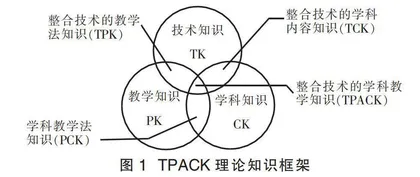
TPACK（Technological Pedagogical Content Knowledge）即整合技术的学科教学知识，由学者科勒和米什拉于2005年在舒尔曼的学科教学知识PCK的基础上提出的［2］。它包含了学科知识、教学知识、技术知识以及它们相互交融衍生出来的整合性知识（图1），它既强调信息技术的有机组成，又深刻指向学科素养，是物理学科信息技术融合教学的重要理论工具。

SOLO分类理论是由皮亚杰的认知阶段理论发展而来，它提供了可观察的学习成果的结构。该理论将学习成果（思维层次）划分为五个边界清晰且易于测量的结构（图2），包括前结构、单点结构、多点结构、关联结构和拓展结构。这五个结构与高中物理学科核心素养的五个水平相对应，可在TPACK框架下作为融合教学评价的理论工具。

2    速度关联问题微课程前设计

在高中物理必修二“运动的合成与分解”中，速度关联是一个难点。特别是在有约束的情况下，学生更难准确解决该难点。其根源在于学生对于运动正交分解的独立性缺乏深刻的理解。基于此，以一道有约束的“绳”模型速度关联问题为例，运用TPACK框架，整合情境问题、SOLO分类理论、视频分析以及计算机数值模拟等多个元素，设计了一套创新的微课程（表1），力求覆盖学生认知发展的所有水平，以促进学生高阶思维的发展。

3    微课程教学环节实施与评价

3.1    “绳”模型速度关联问题简单情境——前结构、单点结构

如图3所示，通过视频和PPT展示简单的“绳”模型速度关联问题。师生共同探讨速度分解的平行四边形法则，研究了小船与绳连接点的速度及方向，并最终确定将连接点的运动分解为沿着“绳”方向的收缩分运动，以及以滑轮为中心且垂直于“绳”的摆动分运动。需要注意的是，摆动分运动对于滑轮和小船之间的绳长变化没有影响。在这个过程中，学生逐渐形成了矢量运算法则、分运动的独立性以及轻绳长度守恒等方面的单点认知。

3.2    有约束“绳”模型速度关联问题——多点结构

如图4甲所示，两根不可伸长的绳索绕过定滑轮系在木箱上端，两人以竖直向下的恒定速度v0拉绳索，当绳索与竖直方向的夹角均为θ时，求木箱速度大小。

方法一：如图4乙所示，令物体上升速度为v，沿两绳分解，分速度为v1，则有：v=2v1cosθ。由速度关联v1=v0，得v=2v0cosθ。

方法二：如图4丙所示，考虑对称情况，等效为物体沿一根竖直杆上升，速度沿绳和垂直于绳分解，v1=vcosθ。由速度关联v1=v0，得v=v0 /cosθ。

以上两种木箱速度的分解方法均依据矢量运算法则，且沿绳分速度关联相等，为何会得到两种不同的结果？通过此环节引入思维冲突，激发学生形成对矢量投影和正交独立性各知识点的关联认知。

3.3    利用视频分析和数值模拟进行实证研究——关联结构

师生共同探讨了对以上结果进行验证的技术手段，包括频闪照相、速度传感器、视频分析软件Tracker以及常用办公软件WPS等。

第一小组学习了如何使用Tracker软件，包括创建质点、自动搜索和分析等步骤。他们录制了视频并将其导入软件进行分析，将质点A的速度进行正交分解，并与质点B的速度进行比较，如图5甲所示。通过分析图5乙的结果，可以得知这两个速度都是变化的，并且变化趋势是一致的。然而，由于软件在角度跟踪分析方面存在误差，手机录像的帧率较低，以及手动拉动物体运动变化不均匀等原因，导致两个速度之间存在差异，无法得出确切的结论。

另一小组则建构了一个理想运动模型，如图6所示。图中，质点A和B分别代表与“绳”关联的两个端点。他们利用WPS进行数值模拟计算，这种方法操作简便易上手，只需在表格中编写公式进行递进运算。虽然这种方法相对比较原始，但它是大型数值计算的基础，有助于提升学生的信息素养水平。

先对系统进行初始化，令d=1 m、v0=1 m/s、θ0=30°，质点B以v0向下匀速运动，计算步进为Δt=0.005 s。质点A的近似速度为v=Δy/Δt，v0 /cosθ和2v0cosθ两值取Δt内初、末时刻速度的均值。对比这三个速度计算值，结果如表2所示。

对表2分析可知，方法二的结果是正确的。若将质点A的速度沿两绳分解，由于两分量并非正交，另一分量对沿绳分量的“收缩”运动有影响。若将此分量进一步投影到绳方向，可得到v1+v1cos2θ=v0。因此，解决此问题的关键在于“绳不可伸长”这个约束条件。从能量角度看，轻绳对两端点连接的物体做功之和为0，即Tvcosθ-T'v0=0。至此，学生可形成对矢量运算相关知识点的关联认知。

3.4    非正交矢量运算问题——拓展结构

通过以上内容的学习，学生能理解垂直于绳子的摆动分速度不影响沿绳的收绳分运动，即正交情况下两个分运动完全独立。这种矢量的正交独立性在其他矢量运算问题中是否也存在呢？

在如图7甲所示的正交力场中，动能定理可以单独“应用”在竖直方向或水平方向。在如图7乙所示的匀强电场中，建立直角坐标系xOy，已知OA=OB=1 cm，φO=1 V，φA=2 V，φB=0 V，θ=30°。由场强与电势差的关系E=U/d，求得y和OB方向的分场强，再合成出合场强的结果是错误的。

在非正交情况下，电势差的变化不仅与该方向的分场强相关，还受到另一方向分场强的影响，即电势在某个方向上的变化是由合电场决定的。通过解决这个问题，关于“矢量正交独立性”的认知由“速度关联问题”拓展到各类矢量运算，使学生的认知达到了更高的层次。

4    结  语

从有约束的“绳”模型速度关联问题出发，拓展到其他矢量投影问题，突破了思维惯性，使学生从低阶思维向高阶认知转变，并利用SOLO分类评价将多个维度的素养整合在一起。开创了高中物理创新微课程的新思路和新方式，有助于物理学科核心素养的培养。

参考文献：

［1］中华人民共和国教育部.普通高中物理课程标准（2017年版2020年修订）［S］.北京：人民教育出版社，2020.

［2］黄全安，郭洋.TPACK视角下高中物理教学的路径优化——以“自由落体运动”教学为例［J］.物理教学，2024，46（2）：16-20.

［3］Deng X M，Wang M H，Chen H L，et al. Learning by progressive inquiry in a physics lesson with the support of cloud-based technology［J］. RESEARCH IN SCIENCE & TECHNOLOGICAL EDUCATION，2019（6）：308-328.

（栏目编辑    贾伟尧）