DIS实验助力模型建构

摘   要：在绳速度分解模型中，辨别绳速度为合速度还是分速度是教学的难点，也是学生的易错点。利用DIS实验装置助力绳速度分解的模型建构，将实验数据图像与正确和错误的理论分析图像进行对比验证，使学生更加直观地感受正确的绳速度分解方式。DIS实验助力课堂理论分析的教学方式有利于加深学生的模型建构能力，培养学生的科学探究和推理论证能力。

关键词：模型建构；绳速度分解模型；DIS实验

中图分类号：G633.7 文献标识码：A     文章编号：1003-6148（2024）11-0051-6

１    引  言

高中物理中，速度分解问题属于运动学的一部分，是分析物体运动规律的基础知识之一，也是高考重要的考点。但是，相关习题的形式多种多样，要求学生灵活运用水平竖直正交分解和按实际效果正交分解的方法。学生常常在判断是否需要按实际效果进行分解，以及如何按照实际效果进行分解两个方面出现问题。尤其是在绳速度分解的问题上，很多学生会不知道如何分解绳的速度，甚至不知道应该分解哪种速度［１］。因此，教学中教师不仅应该带领学生进行理论推导，还应该通过实验的方式，让学生更加直观地感受哪一种绳速度分解才是正确的情况，从而激发学生的学习兴趣。

近年来，随着科学信息技术的发展，数字信息化实验（ＤＩＳ）逐渐被引入实际教学课堂。ＤＩＳ实验通过传感器、数据采集器和计算机等设备实时将实验数据传递到计算机上，具有高灵敏度、高采集速度等优点，因此可以很好地解决传统实验中存在的一些问题［２］。

本文利用ＤＩＳ实验装置，可以很好地观测绳端点速度的变化情况，并对实验结果进行分析，助力学生更加直观地感受绳端点速度是如何分解的，从而提高教学质量。

２    绳速度分解的模型建构

２．１    速度分解

速度分解是指将一个物体的速度按照不同方向分解成多个分速度的过程。在高中习题中，通常可以用两种方式进行分解，即水平竖直正交分解和按实际效果正交分解。

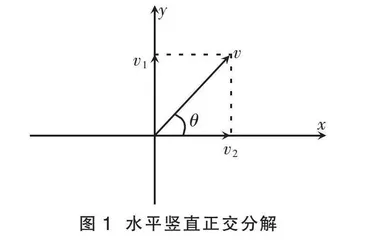
水平竖直正交分解，通常是指将原始速度分解成水平方向和竖直方向上的速度。例如，一个物体以速度v斜向上运动，可以将其速度分解成竖直方向上的分速度v1和水平方向上的分速度v2，如图１所示。

按实际效果正交分解则是根据原始速度的实际现状，分解成两个既不水平也不竖直的速度。如图２所示，一个物体与斜面成一定夹角，以速度v做斜抛运动，可以将其速度分解成沿着斜面方向的分速度v1和垂直于斜面方向的分速度v2来进行研究。

２．２    绳或杆速度分解问题

绳或杆速度分解问题，是运动的合成与分解中的一个难点，也是易错点。解决绳或杆速度分解问题的关键是确定运动对象，判断什么是关联速度。关联速度是指当两个物体通过绳或杆的连接运动时，两物体沿绳或杆方向上有分速度，此时两个分速度的大小相等。绳杆关联速度模型具有三大特点，分别是绳或杆质量忽略不计，绳或杆不可伸长，沿绳或杆方向的速度分量大小相等。

２．３    解决绳或杆速度分解问题的一般步骤

（１）确定对象：确定需要进行运动分解的对象。（２）找关联点：物体和绳或杆的连接点。（３）找出物体实际运动速度：先确定物体的实际运动，即物体的合运动，判断应该对哪一个速度进行分解。（４）分解合速度：确定合运动的两个实际作用效果。一种是沿绳或杆方向的平动效果，这个效果改变速度的大小；另一种是沿垂直于绳或杆方向的转动效果，这个效果改变速度的方向。将合速度按照这两种实际效果进行正交分解，即沿绳或杆方向的速度和垂直于绳或杆方向的速度。（５）进行求解：根据沿绳或杆方向速度的大小相等列方程求解。

２．４    常见的模型

（１）一绳一物模型：如图３所示，绳与物不在同一水平方向上运动，物体沿着轨道向左运动。对物体末端速度ｖ分解，将物体的实际运动速度分解为沿绳收缩方向上的速度ｖ１和垂直于绳方向的速度ｖ２。此时，沿绳方向的分速度ｖ１就是绳子收缩时的速率，即拉绳的速率，v=［３］。

但在日常做题过程中，学生在思维定式的影响下，容易认为所有的运动都可以按照水平和竖直的方向进行分解，错误地认为沿绳收缩方向的速度为合速度v，将绳速度分解为水平和竖直两个方向的分速度（图４），v1=vcosθ。

（２）两物一绳模型：两物通过细绳跨接在定滑轮两侧，同时向左运动。两物与绳的速度均不相同。在定滑轮两侧绳子的速度方向也不相同。在绳子末端两个物体的速度都需要分解。根据前面介绍的绳杆关联速度模型的特点之三，可知两个物体在沿着绳子方向的分速度大小是相等的。如图５所示，即vA2=vB1。

（３）两物一杆模型：在杆两端物体的运动速度不相同，A点向下运动，B点向右运动。将杆的两个端点A、B的速度沿杆和垂直于杆的方向进行分解，则A、B两点沿杆方向的分速度大小相等。如图６所示，vA1=vB2。

３    ＤＩＳ实验助力难点突破

３．１    难点分析

以上介绍的是常见的几种连接体问题的速度分解方法，模型建构清晰，图像也很直观。但是，在教学中往往发现学生还是不知道哪个才是合速度，不清楚应该分解哪个速度。其原因除了可能没有理解速度分解的基本原理，即速度分解应该分解的是物体运动的实际速度，而不是基于思维定式全部按照水平竖直的分解方法进行分解；还可能是问题本身比较抽象，而现实中又没有简便的方法来直观验证正确和错误的速度分解结果，即正确与错误都只是停留在课本和习题答案上。如果教师在教学过程中能将理论推导和实验论证与直观的物理现象联系起来，让学生从理论和实验两个角度来看待同一个问题，可能会加深对物理问题的理解，提升学生的物理思维能力，同时也能提高学生的探究能力和推理论证能力。接下来，我们以一绳一物模型为例，介绍和讨论如何利用ＤＩＳ实验来助力模型建构中的难点突破，让学生“看见”正确的速度分解，从而改善学习效果。

３．２    ＤＩＳ实验

实验装置如图７所示，由两个力学导轨、四个光电门、两个小车、若干铜线、电机组成。

由图３和图４可以看出，假设绳速度为分速度时，绳速度应该小于小车的速度，绳速度应该在小车运动速度的下方；假设绳速度为合速度时，绳速度应该大于小车的速度，绳速度应该在小车速度的上方。具体情况及图像如表１所示。为了更好地让学生直观感受绳速度的分解情况，我们利用ＤＩＳ实验设备将实验结果与理论结果进行对比，就可以更加直观地判断绳速度究竟是分速度还是合速度。

图７ 所示实验装置原理是利用电动机的匀速转动，使得小车Ａ匀速向左运动，并带动小车Ｂ向左运动。设小车Ａ和Ｂ匀速运动的速度分别为vA、vB，小车Ｂ的绳索与水平面的夹角为θ时，小车Ｂ的速度分解为两个效果：一是滑轮与小车Ｂ之间的绳缩短，二是绳绕滑轮转动。因此，将小车Ｂ的速度分解为沿绳方向的速度v∥和垂直于绳方向的速度v⊥，即

v∥ =vBcosθ

v⊥=vBsinθ

由于同一根绳上沿绳方向的速度相等，即

vA=v∥

测量得到小车Ｂ到滑轮顶端的高度为h，力学导轨２上的两个光电门到滑轮正下端的水平距离分别为l1和l2。设小车Ｂ经过光电门３和光电门４时，小车Ｂ的速度分别为vB1和vB2，绳子与水平方向的夹角分别为θ1和θ2，对应的cosθ1与cosθ2的表达式

cosθ1=

cosθ2=

综合上述表达式，我们可以得到vA和vB之间的关系

vB=

vB1=vA

vB2=vA

理论上小车Ａ的速度应该一直保持不变，但是因为实验中摩擦力、绳子张力等因素的影响，光电门１和光电门２测量出来的小车Ａ的速度会不一样。为减小误差，选择将光电门１和光电门２测出的速度vA1、vA2的平均值作为小车Ａ的速度，即

vA=

（１）实验数据收集

在实验开始前，通过直尺测出力学导轨２到滑轮顶端的高度差h=11 cm，光电门３到滑轮的水平距离l1=17 cm，光电门４到滑轮的水平距离l2=37 cm。由此，我们可以得到绳子在光电门３处与水平方向的夹角的余弦为cosθ1=0.839 6，光电门４处与水平方向的夹角的余弦为cosθ2=0.958 5。

在将4个光电门与数据收集器相连接后，遮光片通过不同光电门所用的时间会被传导到计算机，如表2所示。其中，t1、t2、t3、t4分别为通过光电门１、２、３、４所用的时间。

根据t1、t2、t3、t4以及遮光片的宽度2 cm，可以分别得到小车通过4个光电门时的平均速度vA1、vA2、vB1、vB2，如表3所示。

（２）实验数据分析

整理上述数据，并进行理论验算后，得到数据如表4所示。

为了更加直观地感受绳速度分解情况，从三个维度对速度分解情况进行对比分析，分别从绳速度vA与小车通过光电门３的速度v以及光电门３的理论速度v进行对比分析，绳速度vA与小车通过光电门４的速度v以及光电门４的理论速度v进行对比分析，绳速度vA与小车通过光电门４的速度v以及光电门３的速度v进行对比分析，得到图8—图１0。

由图8可见，光电门３的实际速度v（小方块）与以绳速度为分速度计算出的理论速度v（实心原点）相吻合，而与以绳速度为合速度计算出的理论速度v'（倒三角，最下面一条数据线）相差甚远，实验数据很好地验证了一绳一物模型建构的速度分解。

光电门３的理论速度对比分析图

与图8同理，由图9可见，光电门４的实际速度v（小方块，第一条数据线）与以绳速度为分速度计算出的理论速度v（实心圆，第二条数据线）相近，而与以绳速度为合速度计算出的理论速度v'（倒三角，最下面一条数据线）相差甚远，实验数据较好地验证了一绳一物模型建构的速度分解。此处光电门４的实际速度与以绳速度为分速度计算出的理论速度（即第一条数据线与第二条数据线）理应如图8所示的一样重合，但实际上并没有。分析可能的误差来源有三点：①小车在运动过程中绳本身会带有一定的弹性（伸缩性），会影响小车的运动情况；②相比光电门３，光电门４处绳子与水平方向的夹角θ更小，导致测量误差更大；③光电门测得的速度为平均速度而非瞬时速度。

光电门４的理论速度对比分析图

图１0可以更直观地看出绳速度vA（正三角，最下面一条数据线）为分速度，因为光电门３的实际速度v（小方块，第一条数据线）和光电门４的实际速度v（实心圆，第二条数据线）都比绳速度要大，且光电门３的实际速度与光电门４的实际速度曲线都更加贴合表1所示的vB=的理论速度曲线。除此之外，因为光电门３对应的θ1比光电门４对应的θ2大，相对应的v大于v，与绳速度为分速度的理论推导相符合，从侧面验证了实验结果的可靠性。

综合以上数据，结合理论分析，我们可以清晰地看到，小车Ａ的速度，即绳收缩的速度应该为分速度，小车Ｂ的速度为合速度。在实际运动过程中，小车Ｂ的速度应分解为沿绳方向和垂直于绳方向的两个速度。

４    结论与展望

通过上述实验我们可以看出，通过ＤＩＳ实验的定量研究，可以更加直观、形象地帮助学生判断合速度和分速度以及绳速度分解模型中速度的正确分解方法，即应将物体的实际运动速度分解为沿绳方向和垂直于绳方向的两个分速度。由此我们可以发现，ＤＩＳ实验的有效利用可以帮助学生更好地理解物理现象和物理知识，将模型建构中较抽象的物理理论计算转化为能够可以直接观测到的物理现象和物理实验数据。因此，将ＤＩＳ实验引入到实际课堂习题讲解过程中，将会有利于提高学生对物理课程的兴趣，培养学生对物理实验设计的更多思考和科学探究的能力，有利于培养学生的创新意识和创新能力，从而真正理解物理。本文仅以绳速度分解的模型为例，但本文的方法和思路可以推广到其他情况中。

参考文献：

［１］陈丁丁．高中物理速度分解问题的探究［Ｊ］．数理化解题研究，２０２２（６）：８６－８８．

［２］黄晓博，呼格吉乐．传统实验与ＤＩＳ实验在高中物理教学中的对比研究——以“平抛运动”实验教学为例［Ｊ］．中学物理教学参考，２０２３，５２（１２）：６７－６８．

［３］庄步华．关联速度模型中的三种解法［Ｊ］．中学物理教学参考，２０２２，５１（２１）：６５－６７．

（栏目编辑    刘   荣）