探“图形运动”本质 促“整体建构”关联

［摘  要］ 研究者通过分析学生学习“旋转三要素”前后的测评数据，整合“线与面的旋转”教学内容，渗透“图形旋转即点旋转”的本质认知，在沟通与对比中不断提升学生的空间观念。

［关键词］ 整体建构；图形的旋转；运动本质；空间观念

小学阶段“图形运动”包括三个教学内容：轴对称、平移和旋转，教材基于从易到难、螺旋上升的原则进行编排。“旋转”是“图形的运动（三）”中的内容，它是小学数学“图形的位置与运动”板块最后一个学习内容，“旋转”与对称、平移相比更抽象，涉及的要素更多。在教学“图形的旋转”时，大部分教师先教学“线段旋转”，后教学“图形旋转”。因此，笔者产生了一些思考：基于整体建构视角，能否将线段教学融入图形旋转教学中？是否按先转三角尺再画三角形的思路教学？基于以上思考，笔者通过对比多种教学路径，基于真实学情从整体视角出发重组了教学内容。

一、教学序列的分析

“图形的运动”以轴对称、平移和旋转等载体通过全等变换，让学生进一步把握图形运动的特征，从而有效发展空间观念。内容要求、学业要求、教学提示都指向了让学生用“旋转三要素”描述图形的位置，用方格纸画简单的图案，感受旋转的特征。

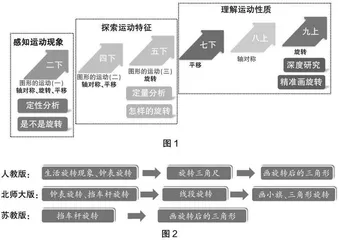
1. 教材对比

（1）教学序列的纵向分析

“图形的运动”在各个学段的人教版教材中都有所涉及（如图1所示）：二年级，能初步感知旋转的现象，能定性判断“是不是旋转”；五年级，能用“旋转三要素”从定量的角度精准描述“怎样旋转”及尝试画简单的旋转图形；九年级，直接借助圆规和量角器作图。

（2）教学序列的横向对比

笔者对比了人教版、北师大版、苏教版三个版本的小学数学教材，对情境、素材、路径等方面进行了异同点对比分析（如图2所示）。

①相同教学思路

相同点1：基于生活原型，明晰“旋转三要素”。人教版教材借助指针旋转，北师大版、苏教版教材利用停车场转杆等生活情境来认识“旋转三要素”。

相同点2：操作探究，深化旋转本质。三个版本教材都是借助摆一摆三角尺来渗透旋转本质。

相同点3：关联点、线、面旋转，凸显结构化思想。教材关注了点、线、面的旋转，深化“图形旋转的本质即点的旋转”。

②不同教学路径

“图形的旋转”教学的路径不同：人教版先教学旋转三角尺再画三角形，北师大版先教学画旋转线段再画旋转后的图形，苏教版直接教学画旋转后三角形。

2. 学情分析

笔者对147名学生进行了两次测试，具体情况见表1、表2。

分析测试结果发现，学生对于“旋转三要素”的认知存在较大偏差，能感知线的旋转，但对面的旋转不够明晰和完整。

针对这样的数据，笔者产生了思考。

（1）教学“旋转三要素”后，能否直接进入“面的旋转”教学？

学习“旋转三要素”后，学生画旋转线段准确率从64.63%提升至89.80%，表明学生对于画线段并无太大难度。画旋转线段后的三角形实际上是让学生经历找点、连线、成面的过程，发现点、线、面不是分离的，从而建构整体性的认知。因此，直接教学“面的旋转”更有利于学生建构整体的认知。

（2）依托数据，把三角尺能否融入旋转画图教学？

在学习“三要素”后，有59.86%的学生不借助三角尺的旋转也能正确画图。能否不再单独教学三角尺的旋转，而是将三角尺作为学习支架整合到“图形的旋转”教学中？这样的设计能够带来两大便利：一是“放一放”，让会画的学生利用空间想象画图，使三角尺起验证作用，充分发展学生空间观念；二是“扶一扶”，作为一个有力的学习支架，让有困难的学生先旋转三角尺再画图。

二、单元序列的重组

基于这样的思考，笔者在教学“三要素”后直接教学“图形旋转”，将三角尺、线段融入画三角形的教学中；第二课时为“图形的分析”，利用图形运动知识分析图形，根据情境需要灵活分解基本图形，培养学生解决问题的实践能力；第三课时为拓展课“图形的设计”，以设计“美丽的图案”为主线，经历多个图形拼组的运动变化，培养学生空间想象能力。

三、关键课例的实践

“图形的旋转”是本单元的关键课例，教学重点为“认识旋转三要素，正确画出旋转90°后的三角形”，教学难点为“理解图形的旋转本质”。

1. 遵循教材：生活情境，认识“旋转三要素”

（1）寻求共同点，初识“旋转三要素”

师：如图3所示，这些运动都是旋转吗？有什么共同点？

生1：都绕着1个点旋转。

师：谁能上来指一指？

师：我们称它为旋转中心。还有其他发现吗？

生2：向左或向右转。

师：谁能来演示一下？

师：看来旋转还要有方向，数学上有专门的名词叫顺（逆）时针旋转。

师：观察钟摆跟转杆，你们还有什么发现呢？

生3：它们都旋转一定的角度。

小结：通过对比这几幅图，发现都有中心点、方向和角度，这就是“旋转三要素”。

设计意图：数学源于生活，应用于生活。本环节教师利用生活情境导入，让学生在辨析中逐步认识“旋转三要素”。

（2）描述初尝试，话说“旋转三要素”

师：二年级时我们学会判断旋转，现在是五年级了，可以用“旋转三要素”描述旋转。

师：如图4所示，你们能用“旋转三要素”说一说转杆是怎么旋转的吗？

生4：顺时针旋转90°。

生5：转杆绕点O按顺时针方向旋转90°。

师：现在呢？

生6：转杆绕点O按逆时针方向旋转90°。

师：大家都看得懂指针吗？12到6，它怎么转动？

生7：指针绕点O按顺时针方向旋转180°。

师：现在同桌相互说一说，让指针从几到几，它怎么转动？

要求：从（    ）到（    ），指针绕点（    ）按（    ）方向旋转（    ）。

生8：从12到12，指针绕点O顺时针旋转360°。

生9：从6到8，指针绕点O顺时针旋转60°。

师：用“旋转三要素”描述旋转有什么好处吗？

生10：描述更精确。

设计意图：本环节教师引导学生用“旋转三要素”描述生活中的旋转，让学生在描述的过程中感受用“旋转三要素”描述的精确性。

2. 合理融合：简单图形，画“旋转三要素”

师：线段的旋转对你们来说太简单了！下面，我们直接学习“三角形的旋转”。

师：线段OA绕着点O按顺时针方向旋转90°，你能画出来吗？

教师展示任务要求，如图5所示。

（1）错误辨析，明晰正确画法

作品1：中心点错误。（教师利用透明三角形演示，按着中心点旋转）

师：旋转的时候绕着中心点，这个点是始终不动的。

作品2：长度画错。（学生利用透明三角形演示）

师：看一看前后长度有变化吗？

生11：没有。

师：那另外两条呢？

师：旋转的时候形状大小不变，边的长度也不变。什么变了？

生12：方向、位置。

作品3：画成轴对称图形。

师：猜猜看，他想成什么运动了？

生13：轴对称。

师：（展示正确作品）画对的同学请举手，谁能说说怎样才能又快又准地画旋转图呢？

生14：找点A′、点B′，再连线。

师：点A与点A′可以称为是一组对应点，怎么找到点A′的？

生15：数格子。

生16：先找到旋转90度后的线，然后数格子。

师：真厉害！我们找到了点A和点B的对应点A′及点B′，然后与中心点O连线就可以画出旋转后的三角形！现在给你们一点时间对自己的作品进行调整。

设计意图：本环节教师引导学生尝试画旋转后的三角形，呈现学生的典型错误，让学生在辨析中从关注面的旋转到关注线的旋转，并明晰画法。

（2）由外到内，感受图形特征

师：刚才利用3个点画了三角形，那三角形上只有这3个点吗？

生18：我在三角形的边上可以找到1个点。

生19：我在边上可以找到3个点。

生20：线段是由无数个点组成的，3条边上可以找到很多点！

师：只能在线段上找吗？

生21：我在三角形内部也找到1个点。

生22：三角形是由无数个点构成的。

设计意图：画法明晰之后，本环节指向图形运动的深度解读。教师引导学生从关注3个特殊点到图形的所有点，为后续理解图形运动的本质做好铺垫。

（3）从面至点，渗透运动本质

师：这个点怎么运动（在直角边AO上标出点C）？

生23：绕着点O顺时针旋转90°得到C′。

师：其他点也这样运动吗？能找出几组对应点来验证一下吗？

作品1：找到2条直角边上的点。

生24：都是绕着点O顺时针旋转90°。

作品2：找到内部的点。

生25：也都是绕着点O顺时针旋转90°。

师：可以怎么验证？

生26：用三角尺的直角进行验证。

生27：还可以用量角器验证。

作品3：斜边上的一点。

生28：好像是绕点O顺时针旋转90°。

师：一下子分不清，我们用几何画板进行演示。

生29：都是绕点O顺时针旋转90°。

小结：图形绕着点O顺时针旋转90°，就是图形上所有的点也都绕着点O顺时针旋转90°，所以旋转后图形的形状、大小不变。

设计意图：本环节教师引导学生从关注面到关注线再到关注点，借助几何画板从边上的点到内部的点延伸，感受图形旋转的本质是点的旋转。

3. 巩固提升：自由创作，用“旋转三要素”

师：敢不敢挑战下自己？刚才三角形AOB是绕着点O顺时针旋转90°，你们还想它绕着哪个点转？还想往哪个方向转？准备旋转多少度？把这段话补充完整之后，开始画一画。

展示任务要求：三角形AOB绕（   ）按（   ）时针旋转（   ）。

课件展示学生作品，如图6所示，由学生逐一汇报。

生30：绕点O逆时针旋转90°。

生31：绕点B顺时针旋转90°。

生32：绕点A顺时针旋转180°。

生33：绕点B顺时针旋转270°。

设计意图：本环节教师让学生自行选择“旋转三要素”，感受“旋转三要素”对于旋转的重要性。在学生各种作品的介绍与展示中，将汇报变成展示过程，让学生在潜移默化中学会学习。

4. 纵横对比：前后衔接，理解“旋转三要素”

（1）图形运动横向对比

师：关于图形的运动，以前学习了轴对称、平移，它们有什么不同之处？

生34：都是运动，但是运动方式不同，分别是翻动、移动、转动。