借助“直观”启发几何问题解决

[ 摘 要 ]文章以三角形中位线定理的再证明为抓手，梳理利用“几何直观”培养学生分析、探究能力的图形表象、实验、知识联想、数形结合等方法，揭示借助“几何直观”发现解决问题方法的基本套路，并应用套路解决新问题，以培养学生的分析探究能力.

[ 关键词 ]核心素养；几何直观；中位线定理

“几何直观”的内容和要求

“几何作为一种理解、描述和联系现实空间的工具，也许是数学中最直观、具体和真实的部分”[1]（Mam？ mana&Villani，1998），所以《义务教育数学课程标准（2022年版）》（下文简称《标准》）把几何直观作为核心素养的主要表现之一.《标准》指出：几何直观要求能够感知各种几何图形及其组成元素，依据图形的特征进行分类，几何直观有助于把握问题的本质，明晰思维的路径.

几何直观是思考问题、解决问题的重要思维方式之一，是直接“从感觉的具体的对象背后，发现抽象的、理想的（状态）的能力”.对几何直观最贴切的表述应该是史宁中教授的：思路是看出来的，不是证出来的[2].这里的“看出”，就是凭借几何直观洞悉几何元素的内在联系，这不仅有助于探索问题解决的思路，而且可以获得对数学的直观理解，抓住问题的本质.

借助“几何直观”解决几何问题的实践

根据直观性的表现，我们是否可以在几何问题中借助直观来认识和理解问题，同时帮助人们探索问题、促进发现呢？如三角形中位线定理，传统课堂在提出“你能根据猜想进行证明吗？”这一问题后，学生直接回答自己的证明方法，然后进入应用环节.这种做法，对学生而言，并没有经历定理的探究过程，只是接受了一种数学事实.实践证明，学生很多时候遇到几何问题解决不了，是卡在第一步，即无从下手，不知道朝什么方向思考，简单地说，就是不知道如何添加辅助线.这就需要学生利用“几何直观”分析和探究问题，找到图形间的内在联系以及解决问题的方向，从而达到问题解决的目的.

为了帮助学生明确对几何图形的直观感受，并且运用这种直观感受，笔者将九年级总复习阶段的学生作为教学对象，以中位线的性质证明的再探究、再经历、再创造、再应用为例，通过如下环节予以说明.

环节一 利用纸片折痕，感受直观内涵.

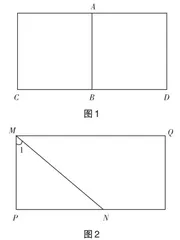
提问 请猜想图1中线段AB与线段CD之间的位置关系，并猜想图2中∠1的度数.

设计意图 将图1所示的矩形沿着AB对折，发现折叠后的BD与

BC完全重合，所以AB与CD垂直.将图2所示的矩形沿着MN折叠，发现边MP与MQ不重合，验证了猜想∠1=45°是不准确的.引导学生认识到一些结论正确与否可通过观察猜想、操作认证这种“直观”的方法予以验证，从而建立直观观念.

环节二 再探中位线，打开直观空间.

提问 上述证法一、二，你是从什么角度想到可以这样解决问题的？

回答 ①看图形很像相似中的“A”型相似，于是尝试用相似来解决；②要证明平行，可以利用三线八角，从而想到利用相似证明角相等；③由“平行且相等”联想到构造平行四边形，只要证明四边形DBCO是平行四边形就可以得到结论.

教学意图 “是这样”“会这样”等直观意识是解决问题的起点，“A”型相似简单、易懂，能让学生感受到直观的魅力、知识的力量；而由“平行且相等”联想到平行四边形，回顾了已学知识，带动了再探究的发生.

2.系统梳理，拓宽直观

提问 抛开中位线定理的证明，看到“中点”“平行”“线段倍分”这些关键词，你会想到哪些相关的知识和方法？

学生表达，教师板书，形成如下思维导图（如图5、图6和图7）.

提问 你发现更多的证明方法了吗？

证法三 （从倍长中线方法中获得灵感）

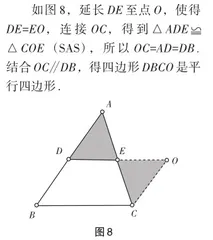
证法四 （从对角线互相平分中获得灵感）

如图9，延长DE至点O，使得DE=EO，连接OC，DC，AO.由于对角线互相平分，证得四边形ADCO是平行四边形.再根据CO∥AD∥BD，CO=AD=BD，得到四边形BDOC是平行四边形.

证法六 （从中点坐标公式中获得利用解析法解决问题的灵感）

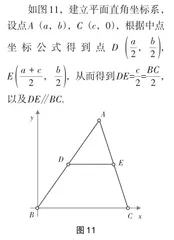
证法丰富，此处不一一罗列.

教学意图 从直观到猜想、验证、证明，是几何学习的基本套路.学生围绕已知证法中包含的关键词的知识梳理，拓展了思路，形成了更丰富的直观观念，其中解析法的直观、简明，让学生获得了更愉快的学习体验，为之后问题的解决提供了更丰富的直观路径.

环节三 借助直观思维，解决真实问题.

问题 如图12，四边形ABCD是边长为8的正方形，点E在边AB上，BE=6，过点E作EF∥BC，分别交BD，CD于G，F两点.若M，N分别是DG，CE的中点，求MN的长.

（课堂上，学生展示其看到的、想到的、直观分割的，猜测、验证并证明）

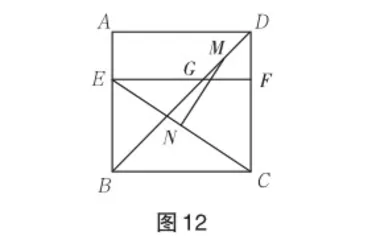
解法一 （利用“图形表象”中的“正方形垂直特性”获得图形直观）

如图13，利用垂直分割，过点 M，N分别作BC，DC的垂线，构成三边长分别为3，4，5的直角三角形MNO.

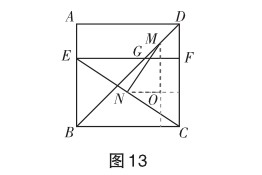
解法二 （利用“知识联想”中的“中位线”获得思路直观）

如图14、15，学生观察发现题目中出现两个中点，但是两个中点没有出现在同一个三角形中，故而想到利用矩形的对角线构造中点，形成新的中位线解决问题.图14中的MO，NO分别是△GCD和△EGC的中位线，图15中的MO，NO分别是△EGD和△ECD的中位线，它们均构成三边长分别为3，4，5的直角三角形MNO.

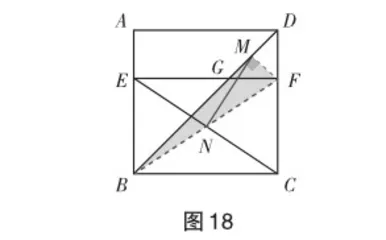
解法五 （利用“拟实验”中的“测量”，结合“知识联想”中的“中线”获得直观）

解法四中学生测量后发现MN的长度大致是5，有些学生直观联想到矩形的对角线相等，那么MN除了是EC长度的一半，是否也是FB长度的一半呢？如图18，连接MF后，只要证明△MBF是直角三角形即可.朝着观察猜想的方向努力，自然发现MF是等腰直角三角形DGF的中线，易得△MBF是直角三角形，从而得解.

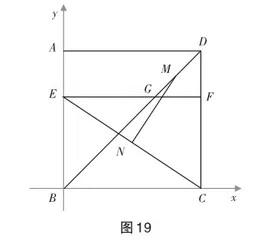
解法六 （利用“数形结合”获得代数直观）

如图19，建立平面直角坐标系，首先可以得到点E，C的坐标，又因为DB是正方形的对角线，于是易得点D，G的坐标，利用中点坐标公式可得点M，N的坐标.最后利用两点间的距离公式或构造直角三角形都可以很快得解.

教学意图 应用是检验教学成败的有效手段，通过直观建立起的观念能不能在问题解决中发挥作用，是衡量本节复习教学有效性的一个重要因素.本环节与前期探究紧密结合，学生分享所悟、所猜、所证，如解法一的垂直分割、解法四通过测量猜想△EMC是等腰直角三角形、解法六的以数定形的数形结合等，都体现了利用各类方法获得几何直观后处理问题的有效性，利用解法的多样性使得几何问题成为思维训练的良好素材.

学生通过“垂直分割试一试”“我感到它是……”“我量一量发现……”等直观的学习方式找到了问题解决策略，实现了直观路径多元，解答策略多样.

利用“几何直观”培养分析、探究能力的方法

（一）以已有知识作为“几何直观”的培养起点

在初中几何学习中，学生往往先利用经验、直觉去推理，就像本课例中，有的学生利用中点倍长中线、构造中位线，有的学生利用中线构造直角三角形，这些都是建立在学生已有的数学经验之上的.接着，在教师所设计的问题引导下，学生探究新的数学策略，解决新的问题，形成宏观认识.从学习心理上来看，这样的教学设计对学生建立数学学习的认识，并化解不必要的心理障碍是有利且有效的.

本节课中，我们尝试利用中位线定理的证明，将“碎片化教学”整合起来，通过学生独立思考、交流方法逐步感悟数学思想方法.不要仅仅成为做题的机器，不要迷恋解题上的一招一式，要注重过程中的通性通法.当学生独立面对一个数学对象时，要学会如何研究一个数学对象，明白研究内容、思路和方法是什么，初中几何教学要注重学生几何直观的发展.

（二）获得“几何直观”的策略

1.利用“图形表象”获得图形直观

根据学生对图形的认知可以将几何概念划分为以下三个层次：最低层次是直观概念，这一层次一般只涉及图形的形状，而与图形元素的性质和关系无关；第二层次属于分析层次，不仅需要观察图形的直观，更要对图形的位置与度量特征等进行分析；第三层次是一些由公理系统所“生成”的，也就是由几何推理得到二级结论[2].

学生处理几何问题多停留在最低层次，而初中阶段的综合性几何问题，要求学生达到更高层次，所以在对图形进行观察后，教师应及时引导学生对图形中的条件进行组合，得到一些基本图形.视觉是一种直觉（有时对发现证明是必需的）的工具.例如环节三中存在矩形AEFD、矩形EBCF、等腰直角三角形EBG、等腰直角三角形DFG、等腰直角三角形ABD等，这些基本图形的得出可以帮助我们在解题时得到一些有益的结论，例如：连接MF，则MF与DG垂直；连接BF，则BF=EC，N为BF的中点等.