初中数学项目式学习的设计与实施

[摘  要] “足球中的数学奥秘”通过设置情境，引导学生在自主探索的过程中逐步建构起数学学科核心知识，并且迁移到新的问题的解决过程中，呈现了数学学科项目化学习的主题确立、目标确定、活动方案设计与实施、成果展示及评价等各个环节的做法和经验.

[关键词] 数学学科;项目式学习;足球;多面体

《义务教育数学课程标准（2022年版）》（以下简称“数学课程标准（2022年版）”）明确指出第四学段7～9年级的学业要求：经历项目式学习的全过程. 其中包含“能综合运用数学和其他学科的知识与方法，在实际情境中发现问题，并将其转化为数学问题;能独立思考，与他人合作，提出解决问题的思路，设计解决问题的方案”等要求[1]. 项目式学习作为现阶段数学教学改革的新课题，成了教师教育教学中关注的热点问题.

然而，如何发掘合适的项目，成了项目式学习的关键和难点. 九年级上册阅读材料“美妙的镶嵌”中涉及正多边形内角的计算、镶嵌方案的设计等数学知识在房屋装修、美学中的应用问题. 本项目将“平面镶嵌”拓展到“空间搭建”，结合时事热点“卡塔尔世界杯”，探究了足球结构中的数学问题，开展了符合学生兴趣，能够促进学生用数学的眼光观察世界的项目式学习的实践.

项目背景

电视节目《最强大脑——寻找阿基米德》播出后，“阿基米德多面体”这个神秘的名词一下子火了. 在《最强大脑》节目中，作为“32进24”环节的考题，阿基米德多面体难倒了很多脑力高手. 一时间，网上出现许多关于阿基米德多面体的热议，就连2019年高考数学全国卷Ⅱ中也出现了有关阿基米德多面体的考题. 这又把阿基米德多面体推到了舆论的风口浪尖，学生对这个话题有着强烈的探索欲望.

足球的原型——“足球烯”就是一种阿基米德多面体（半正多面体），借着2022年卡塔尔世界杯举办的契机，本文的实践中开启了整个项目. “足球中的数学奥秘”以足球为载体，通过对足球的探究一步步揭秘“柏拉图多面体”和“阿基米德多面体”的搭建规律和搭建方法. 通过项目探索加深学生对核心知识的了解的同时，培养学生几何直观和空间观念的数学核心素养，让学生体会神秘的数学背后的文化之美. 本项目探究的是“足球”本身的数学结构，跨数学和艺术两大学科领域，契合项目式学习关注现实问题的解决、关注跨学科、关注数学表达等要求.

项目设计和目标

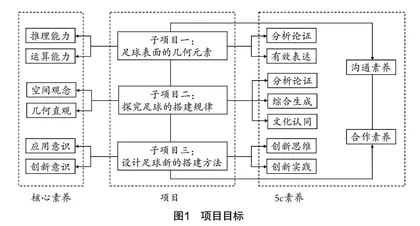
为确保项目式学习的顺利开展，突出项目式学习的特点，本项目的设计包含三个子项目. 各个项目的设计既侧重数学学科核心素养的达成，又兼顾5C素养目标的落实（如图1）.

活动方案及实施

（一）前期准备

1. 教学前学习：文献+网络，学习阿基米德多面体、柏拉图多面体、欧拉公式等相关知识.

2. 材料：《世界杯历届官方用球》视频资料.

3. 思维工具：磁力片——正三角形×20，正四边形×18，正五边形×12，正六边形×20.

4. 分组分工：对学生进行分组，6人一组，组内自主完成分工（表1）.

（二）实施过程

1. 问题驱动

观看视频《世界杯历届官方用球》，从1930年的乌拉圭到2022年的卡塔尔，共22届世界杯比赛. 直到1970年墨西哥的第9届世界杯，国际足联才正式引入世界杯专用足球的概念（如图2）. 而这种设计从1970年一直沿用到2002年，在2018年又卷土重来. 可见，1970年的这种足球设计是使用次数最多、应用最广的. 该足球（电视之星，如图3）由32块黑白相间的正五边形（黑）和正六边形（白）组成，配合均匀的缝制使足球拥有更加浑圆完美的外形. 这也是我们最常见的足球类型. 由此，你能提出哪些值得研究的问题？

通过学生提出的问题将本项目探究的方向落在：足球为什么用正五边形和正六边形拼接而成？用其他的正多边形可不可以呢？这种拼接的优势在哪里？

设计意图  入项是学生进入项目学习内动力的开始. 入项要让学生真正喜欢这个项目，产生问题意识，对驱动问题有内在的探索欲和求知欲，主动地投入项目之中. 通过观看视频，引发学生对足球设计的好奇，引导他们自己提出问题，培养其问题意识的同时，激发其探究的愿望和热情.

2. 项目一：足球表面的基本几何元素

我们知道三角形的内角和是180°，那么四边形、五边形、六边形呢？n边形呢？

任务1：探究多边形的内角和与边数n之间有什么关系（如图4）？

我们把各边相等，各内角也相等的多边形叫作正多边形.

任务2：探究正n边形各内角度数（如图5）.

对于七年级学生来说，多边形内角和度数是新知，教师引导学生利用小学已经学过的三角形的内角和是180°完成项目. 学生小组合作探究，并用恰当的方式记录结果，由组长指派组员上台汇报. 教师根据学生的完成情况进行如下的过程性评价（见表2）.

设计意图  通过探究正多边形的内角和，学生经历转化化归的过程，体验解决问题的过程. 在探究过程中学生发现随着正多边形边数的增大，内角度数也会增大，为后续的探究奠定基础.

3. 项目二：探究足球的搭建规律

如果不考虑足球表面的弧度，足球可以抽象为如图6所示的多面体（足球烯）.

任务1：观察这个多面体，每一个顶点是如何构成的？

判断：下列图形哪些可以构成多面体的顶点（如图7）.

由此你发现构成多面体需要具备哪些条件？

学生通过任务1，发现多面体的基本搭建规律. 完成多面体的搭建需符合以下两个基本条件：条件一，每个顶点出发至少要三个面;条件二，把所有与一个顶点相遇的角加起来，它们的和小于360°.

任务2：探究用一种形状的正多边形磁力片搭建多面体的方法并完成搭建.

任务3：记搭建的多面体的顶点数为V，面数为F，棱数为E. 你发现多面体顶点数V、面数F和棱数E之间有什么关系？

学生运用搭建的两个条件，尝试完成用一种形状的正多边形磁力片搭建多面体（如图8）. 在搭建的过程中，学生发现正多面体（柏拉图多面体）只有5个，并根据统计的多面体的顶点数V、面数F、棱数E，发现欧拉定理：简单多面体的顶点数V（vertex）、面数F（face）和棱数E（edge）之间有关系，即V+F-E=2.

教师根据学生的实践情况进行如下的过程性评价（见表3）.

设计意图  研究了足球表面的几何元素以后，进一步从足球结构的一个顶点出发探究足球的搭建规律. 从中发现用一种形状的正多边形搭建的多面体只有5种，事实上这5种多面体都可以作为新的足球结构. 这个探究环节的设计，让学生明确了足球搭建的基本规律，为后续用两种形状的正多边形搭建新的足球结构奠定基础.

4. 项目三：设计足球新的搭建方法

任务1：足球由32块黑白相间的正五边形（黑）和正六边形（白）缝制而成. 请计算黑色块和白色块的数量分别是多少，并用磁力片搭建足球结构.

学生运用方程、欧拉定理等计算足球中正五边形和正六边形的数量，通过组员之间的合作完成足球结构的搭建（如图9）.

任务2：探究用两种形状的正多边形磁力片搭建新的足球结构的方法并完成搭建. （注：可以先考虑从一个顶点出发的各种组合的可能性，再进行搭建）

学生通过由一个顶点出发的多边形的组合的可能性，寻求尽可能多的搭建方法（如图10）. 教师引导学生进行评价，若选作足球结构哪些多面体比较合适，并说明理由.

任务3：说明足球采用“正五边形+正六边形”结构的合理性.

教师展示图片（如图11），说明本节课中学生搭建的多面体都可以用来作为足球结构. 学生通过项目化学习的过程和体会，交流自己的看法，教师根据学生的探究情况进行如下的过程性评价（见表4）.

设计意图  学生经历了“柏拉图多面体”的搭建后，进一步体会搭建的基本原则，并以此为基础探究足球结构中的搭建奥秘. 进而，通过项目化学习的各个过程思考“正五边形+正六边形”结构的合理性.

5. 终结性评价

教师根据学生完成整个项目的情况进行如下的终结性评价（见表5）.

本次“足球中的数学奥秘”项目的开展，是课堂教学改革的重要尝试. 项目主题容易激发学生的问题解决主动性. 基于问题的活动设计、方法指导、过程引导、成果展示为学生有效实施目标、最终成功解决问题提供了支持和保障.

本项目化学习课例仅展示了部分内容，后续还将针对“足球场中的数学”“赛程（比赛场次）设计”“传球站位和角度”“射门时球的弧线”等展开持续研究.

参考文献：

[1]中华人民共和国教育部. 义务教育数学课程标准（2022年版）[M]. 北京：北京师范大学出版社，2022.