数理同频共振,构建新型实验教学模式

[摘  要] 教师引导学生从观察凸透镜成像的现象中总结规律，形成猜想，然后依据实验操作抽象出光路图（构建几何模型），再尝试运用数学知识证明猜想. 从直观感知凸透镜成像的过程，上升到画图探求凸透镜成像的原理，以此为例构建起一套新型的实验教学模式.

[关键词] 实验;建模;论证

《义务教育数学课程标准（2022年版）》指出：项目学习教学以用数学方法解决现实问题为主，其目标是引导学生发现解决现实问题的关键要素，用数学的思维分析要素之间的关系并发现规律，培养模型观念，经历发现、提出、分析、解决问题的过程，培养应用意识和创新意识[1]. 为了推进新课程标准的落地实施，在充分酝酿准备的情况下，我校在2023年10月举办了项目式学习教学研讨活动，其中由一名数学教师执教的一节物理实验课引发了关注和热议. 下面结合案例进行评析说明.

教学内容简析

教学内容来自初中物理教材第五章“透镜及其应用”的第3节“凸透镜成像的规律”. 凸透镜成像的本质是光的折射，成像规律遵循光的折射规律，这是学习本节内容的知识基础. 在分组实验中，教师引导学生从观察凸透镜成像的现象中总结规律，形成猜想，然后依据实验操作抽象出光路图（构建几何模型），再尝试运用数学知识证明猜想. 从直观感知凸透镜成像的过程，上升到画图探求凸透镜成像的原理，实现了物理学现象与几何规律的一致性逻辑链接，这与物理学习中常见的依照实验直观总结规律，再单一应用规律的设计不同（增加了构建模型、证明规律环节）. 由此呈现的前后一致、逻辑连贯的学习过程，将激发学生对跨学科知识体系的自主建构与融合理解，进而促进学生的思维进阶.

系列实验活动及模型构建

实验活动1：探究凸透镜成像的规律

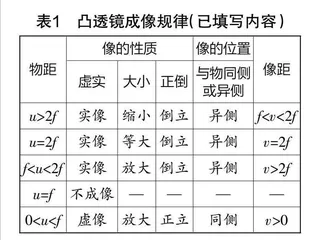
在凸透镜成像实验中观察思考，像的虚实、大小、正倒、位置等与物距的关系. 以小组合作的方式，按设计实验、进行实验与数据收集、形成猜想、分析验证等步骤展开探究，填写表1.

构建模型1：证明凸透镜成像的规律

抽象认识：画出物体的像只需作出物体发出的两条特殊光线即可，一是平行于主光轴的光线，经凸透镜折射后过焦点，二是经过光心的光线，传播方向不改变. 这两条折射光线（或所在直线）的交点就是像的外端点.

如图1，CD代表凸透镜，F1、F2分别代表两个焦点，A′B′为物体AB（u>f）经过凸透镜折射后所成的像，AB∥OE∥A′B′，四边形AEOB为矩形，可得OE=AB.

因为 OE∥A′B′，所以△EOF1∽△A′B′F1，所以==.

因为 AB∥A′B′， 所以△ABO∽△A′B′O，所以==.

又因为 OE =AB，所以=，所以u=.

当u>2f时，即>2f，知v-f>0时有意义，得f<v<2f.

当u=2f时，即=2f，知v-f>0时有意义，得v=2f.

当f<u<2f时，即f<<2f，知v-f>0时有意义，得v>2f.

当u=f时，即=f，无解，v不存在[2].

追问1：当u=f时，图像到底呈现一种什么情况呢？请画图展示（如图2）.

追问2：当0<u<f时，请计算像距的大小.

发现：依据图1得出的关系式u=，当0<u<f时，即0<<f，不等式无意义，为什么呢？

交流：u=是物体与像在凸透镜两侧时，得出的物距u、像距v及焦距f间的关系式，根据表1，当0<u<f时，物体与像在凸透镜同侧，所以不适用于上述关系式.

追问3：图2是凸透镜成实像及虚像的临界情形，与探究凸透镜成实像类似，我们能否借助相应的光路图，得到成虚像时物距u、像距v及焦距f间的关系呢？

如图3，设0<u<f时，物体AB的像是A′B′，知A′B′∥AB∥OE，OE=AB.

因为OE∥A′B′，所以△EOF1∽△A′B′F1，所以==.

因为AB∥A′B′，所以△ABO∽△A′B′O，所以 ==.

又因为 AB=OE，所以=，所以u=.

当0<u<f时，即0<<f，所以v>0. 说明像的位置可能存在多种情况.

追问4：表1中，像高与物高的大小对比情况又如何解释呢？

由图1结论知，当u>2f时，f<v<2f，所以u>v. 又因为==，所以A′B′<AB，即物体所成的像是缩小的像. 类似地，容易得出u=2f，f<u<2f等条件下像的大小变化情况. 当0<u<f时，由图3知==，AB=OE，所以=，又因为f<v+f，所以A′B′>AB，即物体所成的像是放大的像. 关于像的虚实、正倒等问题，上一节课已经学过，这里不再赘述.

教学说明：总结实验现象，去伪存真、去粗取精，形成猜想，进而尝试构建实验模型，小组成员在“实验—构图”的往复中渐渐抽象出实验现象的关键特征，“形”基础得以建立. 图形背景下像距与物距的关系，因为有了表1中的猜想所预示的方向，寻证难度降低了，待发现由平行线确立的相似三角形，其间有等线段关联时，思路豁然开朗，以此为牵引，推理多点“开花”. 本环节教师充分发挥了主导作用，设计了四个递进式“追问”，引导学生拾级而上，逐步铺展延伸路径，不断强化和丰富着“实验现象—图形—关系式”这一探究主线，夯实着三者本质一致性的关系基础，过程中积累的活动经验为探究同类问题提供了示范.

实验活动2：细化探究凸透镜成虚像中物距与像距的关系规律

已知0<u<f时，v>0，实验观察物距u变化时，虚像的位置变化，形成猜想，分析验证后填写表2.

构建模型2：证明凸透镜成虚像中物距与像距的关系规律

由图3知，凸透镜成虚像时物距u、像距v及焦距f间的关系式为u=.

当0<u<f时，即0<<f，得0<v<f.

当u=f 时，即=f，得v=f.

当f <u<f时，即f<<f，得f<v<2f.

当u=f时，即=f，得 v=2f.

当f <u<f时，即f<<f得v>2f.

教学说明：有了实验活动1的铺垫，再类比探究凸透镜成虚像中物距与像距的关系规律，学生的适应性和主动性均有所提高，实验观察及构图推证也会顺利一些，随着雷同解答思路的持续强化，学生将慢慢形成解决问题的“一般经验”. 但是由于实验工具局限性及存在误差等客观因素，如遇到f分界点这类情况，学生在实验中会隐约感知但又纠结于是否准确. 教师可以借此重申，在问题探究中观察到的现象大多算猜想，要想认定所谓“规律”的正确性和一般性，最终还要依靠论证. 当然，实验过程中的操作、观察、尝试等活动在问题解决中同样不可或缺，其作用主要集中在丰富着问题的表象，预示着问题的走向和目标方面.

实验活动3：进一步探究物距变化时，像高变化的规律

在实验1、实验2基础上，进一步探究物距变化时，像高变化的规律，形成猜想，分析验证后填写表3.

构建模型3：证明在一定范围内物距变化时，像高变化的规律

分为物体与像在凸透镜两侧或同侧两种情况：

（1）当物体与像在凸透镜两侧时，满足u>f.

如图4，设物体AB 的像是A′B′，物体AB沿主光轴移动到MN位置时形成的像是M′N′（物体AB移动始终符合u>f），现以O点为原点，主光轴F1F2为x轴，CD为y轴，建立平面直角坐标系.

设F1（ f，0），A（a，b），M（c，b）且a<c<-f<0，则F2（-f，0），E（0，b）.

用待定系数法易求得yEF1=-x+b，yMM′ =x，yAA′ =x.

所以yEF1=-

x+b，

yAA′=

x，

解得x=

，

y=

，

所以A′

，

.

同理可得：M′

，

.

因为a<c<-f<0，所以a+f<c+f<0，于是有-（a+f）>-（c+f）>0 .

所以-<，即A′B′<M′N′.

因此，当物距BO变小时，像高A′B′变大. 再结合表1，可得出表3中u>2f，u=2f，f<u<2f时所列结论.

（2）当物体与像在凸透镜同侧时，满足0<u<f.

如图5，证明过程与（1）类似，易得到A′B′>M′N′，进而得出当物距BO变小时，A′B′变小. 再结合表1，可得出0<u<f时，若u变小，像高随之变小的结论.

教学说明：在图4、图5中，常量与变量交错叠合，有不变的量，如Rt△EOF1的形状、大小，直线EF1的位置等;有变化的量，如Rt△A′B′O的形状、大小，直线A′O的位置等. 观察这些常量位置和变量增减趋势，生出不同的思考视角，这是典型的数形结合思想的体现. 随着AB沿主光轴平移靠近CD，直线EF1不动，另一条直线A′O则呈现绕O点顺时针旋转的状态，动中取静，两直线交点位置的变化一目了然，但是如何将显而易见的现象推证出来，这对学生思维是一个较大的挑战. 建立平面直角坐标系后，线段A′B′，M′N′被进一步“数量化”，用动点A′、M′的坐标表示后，问题豁然开朗，因为字母表达式更具一般性，强调了点变化的连续性和代表性，这种不同于利用三角形相似的函数推证方法，不知不觉间将学生的视野推向了一个新的高度.

教学思考

1. 找准生长“点”，铺设实验论证合理路径

物理实验侧重于现象总结、验证，数学建模更多地展现分析和论证，两者是认识事物的不同阶段，不但不矛盾，还可形成优势互补的局面. 如果不同学科对同一共性问题，仅从自己学科的视角孤立地做出行动，这将限制学生的视野，束缚学生思维的发展. 但是从实验现象“自然”走向分析论证，需要找到问题合适的生长“点”，才不会牵强附会，因此学科融合要搭建好桥梁，控制好梯度，这其中有一个适应、转化、提升的过程. 如实验活动1中，实验现象—形成猜想（表1）—构建模型（图1）—追问1、2、3、4，整个过程中，光路图（图1）是一个合适的初始问题生长“点”，图2、图3是成递进关系的后继生长“点”，这些生长点同在之前“实验现象”及后续“规律推证”的最近发展区内，可自然地链接双方，铺设出较为完整的实验论证路径.

2. 突出优势“点”，展现数理学科不同特点

项目式学习就是以学科之间的共同点为纽带，综合运用数学和其他学科的知识与方法，融合成相互联系、相互照应、穿插进行的体系来探究问题，学科融合不是为了削弱相关学科的优势，而恰恰相反，要坚守和凸显出学科特色，这是由项目式教学中培养学生综合素养的“学业要求”决定的. 物理学习要进行实验，并归纳实验规律，该环节要凸显实验过程中感性认知的积累和升华，体现实验归纳这一物理特色. 到建模论证阶段，从表象到证明规律，数学模型中蕴含的结构特点、知识方法等待解问题随之而来. 如不同的几何模型，不能相互替代，体现了分类讨论的数学思想;解决问题，不同模型采用不同的方法（相似法或函数法），体现了自洽的逻辑一致性;数、式化归时的形式变化，则体现出典型的代数推理特征等.

3. 打造系统“点”，构建新型实验教学模式

项目式学习教学的问题大多具有整体性，解决问题需要多学科的知识技能及方法协同. 本节实验教学已经突破了实验操作、现象归纳的物理常规要求，超越了单门学科的范畴. 由归纳固化实验现象，到构建模型，抽象程度逐步加深，再到后续猜想论证阶段，学生会有意识地反向强化对实验过程的反思，在不断联络和相互赋能中各环节渐渐凝聚，最后浑然成为一体，形成了更有价值的知识系统“点”，构建起一套不同于传统实验教学的新型实验教学模式，具体流程见图6，学生获得有较大意义的研究问题的“一般观念”. 这种“萌芽”式的教学操作，持久地在学生心田“浇灌”“施肥”，学生数学思维的“应用之花”定会灿烂绽放.

参考文献：

[1]中华人民共和国教育部. 义务教育数学课程标准（2022年版）[M]. 北京：北京师范大学出版社，2022.

[2]王晓峰. 对凸透镜成像规律的几点数学思考与探究[J]. 中小学数学（初中版），2022（5）：21.