引导、交流、学习

[摘  要] 教学中要发挥学生的主体地位，教师引导学生主动学习、小组合作交流，在互相交流中学会学习，提升学习能力，真正落实“以生为本”的教学理念.

[关键词] 引导;交流;以生为本

学生的主体地位体现在课堂中以学生为中心进行的教学设计，充分引导学生能够主动探究、主动学习，教师为学生搭建交流的平台，让学生可以在讨论交流中探寻知识. 在交流合作中，让学生可以自己教自己，自己教同伴，实现学会学习，提升综合素质水平. 在教学中，笔者一直在进行这样的尝试，甚至不惜“浪费”时间. 在学习了矩形的性质后，如何继续研究直角三角形的性质，笔者希望先由学生自己进行思考，于是就有了下面的教学实录.

课堂教学实录

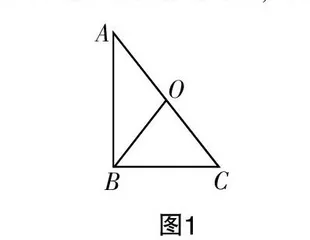
原题：如图1所示，在直角三角形ABC中，斜边AC的中点为O，连接BO，猜想一下AC与BO的数量关系，并进行论证.

师：大家思考后，不知道有没有什么想法呢？有没有人愿意展示一下？

大部分学生有些犹豫不决，继续思考讨论……

师：猜想一下AC与BO的数量关系是什么.

生：AC的长度是BO的一半.

师：我们已经猜想了，那么下面我们需要来论证，有没有同学可以展示一下？

（学生都非常积极踊跃，开始举手）

生1：如图2所示，过点C作CE平行于AB，过点A作AD垂直于CE，垂足为D，连接OD.

师：非常好，那你是怎么想到要作辅助线的呢？

生1：上节课老师带我们学习矩形的性质时，矩形里面有直角三角形，而且也有这样的数量关系，所以我觉得通过构造矩形也可以进行论证.

师：这样的知识迁移运用得非常好，那么通过作辅助线你把矩形构造出来了吗？

生1：是的，通过作辅助线，我得到了三个角是直角，所以是矩形.

（学生窃窃私语：三个角是直角，为什么就是矩形了呢？你是怎么知道的？）

评析 学生学习了长方形的性质，但没有学习长方形的判定，所以结论是学生通过自己的认识进行的猜想. 这样的生成超出了教师的预设，但恰恰是这种“意外”可以真实地反映学生的思考状况，教师不能直接否定，而应该继续引导，调动学生的积极性，鼓励学生敢于表达自己的想法，相信学生自己解决问题的能力.

（生1似乎被难住了，先请他坐下，小组继续讨论）

师：虽然生1给我们提出了一个还没有学习的问题——矩形的判定，但是想一想我们能不能进行转化，用我们知道的图形进行判定呢？

（在教师的提示下，逐渐开始有学生举手）

生2：我觉得三个直角的四边形是矩形，因为我们可以这样进行判定. 因为CE与AB平行，∠ABC是直角，所以∠BCD是直角. 又AD与CD垂直，所以∠ADC也是直角. 因此AD与BC平行，有两组对边平行的四边形是平行四边形. 又∠ABC是直角，所以四边形ABCD是矩形.

（全班掌声一片）

评析 数学概念是解决问题的基础，当学生把问题回归到数学概念中，问题解决就变得轻而易举了. 在教师的引导下，学生利用数学概念突破了这个问题中的第一关，同时学生通过自己的思考获得了一个重要的知识：如果四边形有三个角是直角，那么这个四边形是矩形.

师：同学们经过自己的努力证明了这个四边形是矩形，真是太棒了！那么问题是不是就解决了呢？我们回到最开始的问题，应怎样继续去论证AC与BO的数量关系呢？请生1继续作答.

生1：根据矩形的性质，对角线是相互平分而且相等的，所以AC和BD相等，并且OB和OD都是BD的一半，因此BO是AC的一半.

（生1刚讲完，马上就有学生提出了疑问）

生3：我觉得有问题，BD为什么是矩形的对角线呢？

师：生3讲得好像有点道理，我们可以说明BD一定是矩形的对角线吗？

生4：B，O，D三点不一定在一条直线上，所以我们要证明BD是矩形的对角线.

师：说得非常好，我们不能想当然，需要去证明.

（此时学生纷纷沉默了，课堂氛围严肃了起来）

教师引导学生进行思考和讨论……

评析 通过问题的深入探究，暴露出了学生在思维逻辑上的不严谨、缺乏准确性等弊端，但也正是这样的“意外”的生成，让我们及时发现问题、及时调整教学策略，争取更好的教学效果. 为了使学生的思维更加严密，充分发挥学生的主体作用，应引导学生积极参与教学活动，渗透数学思想和数学方法.

生5：我们可以利用平角来进行证明. 因为△AOD和△COB全等，所以∠BOC和∠AOD相等. 因为∠AOB和∠BOC的和为180°，所以∠AOD和∠AOB的和也是180°，因此可以得到B，O，D三点在一条直线上，所以BD是矩形的对角线.

（生5刚回答好，马上有学生站起来表示有更加简便的方法可以证明∠BOC和∠AOD相等，因为两个角是对顶角，根据对顶角的概念可以证明三点共线）

师：大家对他的说法认可吗？

生：不同意.

师：相等的两个角一定是对顶角吗？这里似乎因果关系搞反了，我们只有在证明了三点共线后，才能得到∠BOC和∠AOD是对顶角的关系. 当然这也不能说明△AOD和△COB全等.

生6：老师，我还有一个想法，可以证明三点共线，不知道对不对.

师：很好，我们不妨来尝试一下，期待你的奇迹.

生6：矩形ABCD中，连接BD与AC相交于点O，根据对角线的性质可得AO和CO相等，因此O就是AC的中点，既然是线段的中点，所以B，O，D三点在一条直线上.

师：说得太棒了，生6给我们打开了一种新的思路. 这种证明方法不常用，但是这种方法有个名称，叫做“同一法”. 其实这个方法以前在证明勾股定理逆定理时使用过，以后我们有时间再讨论. 所以在大家的努力下，我们的问题终于解决了.

评析 学生的潜力是无限的，经过教师的鼓励和引导，学生突破了一个又一个难点，开拓了思维，在智慧的海洋里尽情地遨游. 面对学生一次又一次的尝试，教师要敢于放手，把课堂交给学生，鼓励学生勇敢表达、勇敢试错，才能激发学生无限可能、大胆创新，提高学习效率.

师：经过刚才大家的努力，我们已经成功解决了问题，现在大家回头看一看，通过今天的学习，你有什么收获呢？

生7：我知道了如果四边形的三个角是直角，那么这个四边形就是矩形.

生8：我学到了几种证明三点共线的方法，特别是“同一法”很有意思.

师：同学们说得太好了，我们要感谢同学们提出了这么多有创意的想法，正是因为大家的努力才让我们收获了这么多的精彩. 但是我们也从证明的过程中发现，证明的过程处处都有陷阱，如果不够细心马上就会跳进陷阱，有没有什么办法可以让我们的证明过程更简便呢？

生9：老师，我也构造了一个矩形，但是我的方法更简便：我把BO延长到点D，使DO和BO相等;再连接AD和CD，这样可以证明△AOD和△COB全等，可得四边形ABCD是平行四边形;又∠ABC为直角，所以四边形ABCD是矩形.

师：太棒了，大家寻找到了更加简便的方法. 通过生9的方法，其实我们看到了一个中位线定理，我们一起来总结一下.

生10：直角三角形中，斜边上的中线等于斜边的一半.

生11：我还联想到在直角三角形中，30°的角所对的直角边等于斜边的一半.

……

师：太厉害了，那么关于这些性质的应用，我们将在下节课继续讨论.

教学反思

数学教学应该是在教师的引导下进行的，而不是教师直接把结论交给学生，应该鼓励学生自己去探索，寻找答案，获得知识. 在教学中，有的教师往往害怕生成“意外”，希望一切按照预设、在规定范围内进行，实际上却扼杀了学生的创造性和发展性. 当课堂中遇到学生的一些意外问题时，教师不妨“将错就错”，在此基础上鼓励学生大胆尝试，将猜想进行论证，为学生独立解决问题奠定基础.

在教学中笔者多次鼓励学生交流讨论，敢于质疑，敢于展示自己的想法. 通过学生互相交流，实现效果的最大化. 学生之间互相交流去学习的方式比教师直接传授的方式的效果更好.

学生的潜力是无限的，要挖掘学生的潜能，教师就要不断地去提升自己的专业水平，只有自己的专业能力提高了，才能在遇到学生的意外问题时，游刃有余地进行解决. 总之，只有教师大胆创新，才能激发学生的思维，只有在学生创新思维的基础上，教师才能更好地推进教学.