析典型错解，促深度学习

[摘  要] 以福建省2021年中考卷第20题为例，串联往年同类型题目进行深度分析. 探寻学生解答路径，剖析学生解答情况，挖掘其隐藏思维，给予深度学习提示. 针对此类试题提出数学教学的对策，在教学中培养学生学科思维，让学生能够在 “硬知识”之外，体验更深刻的学科思维方法，进一步提升解题思维的层次性，促进学生知识点和能力点双驱并行和落地生根.

[关键词] 深度学习;思维;错解

福建省2021年中考卷第20题主要是方程与函数的结合考查，从实际情境出发，体现了从情境到数学的数学化过程，既彰显数学价值，也聚焦学生数学运算、数学建模等核心素养的培育. 不管在教还是学，都给予十分重要的地位. 但是学生在答题时候，失分情况频出，比如在计算、逻辑思维、解题习惯等方面，结果并不尽如人意. 笔者以此题为例进行试题串联分析，结合学生答题失误产生原因出发，思考促进学生深度学习的教学对策.

析试题

（一）试题呈现

（福建2021）某公司经营某种农产品，该农产品零售一箱的利润是70元，该农产品批发一箱的利润是40元.

①若该公司某月卖出100箱这种农产品共获利润4600元，问：该公司当月零售、批发这种农产品的箱数分别是多少？

②经营规定，该公司零售的数量不能多于总数量的30%. 现要经营1000箱这种农产品，问：应如何分配零售和批发的数量可以使总利润最大？最大总利润是多少？

本试题知识点包括列方程（组）解应用题、解二元一次方程组、一次函数的性质等. 通过回顾2020年中考卷第20题，发现背景相同，考查内容近乎相似. 现将2020年中考卷第20题呈现如下：

（福建2020）某公司经营甲、乙两种特产，其中甲特产每吨成本价为10万元，销售价为10.5万元;乙特产每吨成本价为1万元，销售价为1.2万元. 因有关条件影响，该公司每月这两种特产的销售量之和都是100吨，且甲特产的销售量都不超过20吨.

①当某月该公司销售甲、乙两种特产的总成本为235万元，问这个月该公司分别销售甲、乙两种特产各多少吨？

②求一个月该公司销售这两种特产所能获得的最大总利润.

本试题知识点考查一元一次方程、一次函数性质等知识. 中考函数类应用题总体上有异曲同工之处，现将其串联进行考点综合分析.

第一问是方程型应用题（2017二元一次方程组，2019一元一次方程及不等式），题目赋予了生活情境，能从学生已有的生活经验出发，让学生感受到数学来源于生活，又应用于生活，彰显了数学的应用价值，有利于引导学生联系生活实际，培养学生的数学应用意识.

第二问是函数型应用题（2018二次函数型应用题，2020、2021一次函数型应用题），综合考查学生阅读素养、提取有效信息、解决问题的能力，充分体现了创新性和综合性强的特点，还关注到初高中数学知识的衔接.

（二）试题评析

方程（组）、不等式（组）及函数是“数与代数”知识领域的核心内容，各知识体系之间联系紧密，数学建模过程也较为类似，考查了学生的数学基本素养及应用能力.

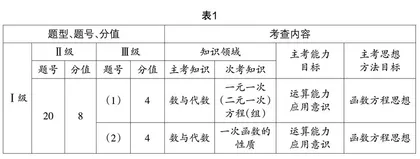
两年中考的列方程（组）解应用题是基于数量关系解决实际问题，呈现的特点如表1所示：

1. 起点低：第一问根据卖出100箱这种农产品共获利润4600元，列出二元一次方程组，解方程组即可. 第①小题相对2020年的考题更容易入手，因为利润是直接给出，而2020年试题利润的计算需要售价减成本得到.

2. 坡度缓：第二问通过题干给出条件可得到零售数量不能多于300箱，难度上升较缓，再通过设问，思考零售和批发的数量的分配，得到最大总利润，从而将考题从考查基础知识向考查数学能力上转换.

3. 关注思想方法：考查学生运算能力、应用意识、函数与方程思想. 分析问题中数量及其关系，以方程或不等式为工具，合理构建数量之间的相等或不等关系是解决实际问题的关键.

找错因

（一）数学学习兴趣缺乏

答题区域直接留白，零基础知识抑或止步于设元，无从下手;这类学生在数学学科学习上缺乏动力和兴趣，解题意志薄弱.

（二）数学运算素养薄弱

1. 运算方法或规则遗忘

本题最较为可惜的是在设元的基础上，能列出正确方程，遇到拦路虎——解方程，计算错误或未计算，导致无法得满分.

还出现这样的情况：设零售农产品为m箱，利润为w，得w=70m+40（1000-m）=30m+4000（或是w=100m+40000）等情况.

2. 运算对象理解的偏差

学生在读题时候，题中出现多个数据，但是他们并未将数据转成相应含义，列式中数据张冠李戴，对于运算对象理解出现偏差. 比如将第①小题列出零售和批发利润混淆，列出错误等式. 第②小题产生错误原因主要在于：一是对于第二问中“1000箱”与第一问中“100箱”没有进一步思考数量作用和条件，还有将第①小题所求得数字“20、80”当成利润参与计算;二是并未弄清楚最大利润的影响因素或存在条件.

3. 运算思路建构遇到关键障碍

运算思路的正确构建是解题核心，其中包括算理、运算对象及运算方法的有机整合. 在本题第①小题，大部分同学选择列方程求解，可以设一个或者两个未知数. 但设两个未知数的前提下，却只列一个等量关系或两个等价方程，二次、一次方程组概念不清，导致无法求出结果.

本题第②小题求的是最大利润，很多学生由于数学阅读能力缺乏，提取有效的信息产生困难;部分学生知道数量是求出最大利润的关键，不能准确根据题中信息获取题干中“不超过300件”，没有关注到“不超过”的数学符号语言转译;很多学生直接选代299，出现代入的错误，导致利润的计算错误. 运算思路的构建遇到关键性的障碍，比如阅读理解能力的问题. [1]

（三）数学建模意识淡薄

函数类应用题以实际背景为轴，将数学知识穿插其中考查. 数学建模并非解决单一问题，而是触类旁通，获得解决一类问题的模型和方法. 很多学生不知道从何入手，不能自主根据不同情境进行数学抽象. 按理来说，2020年中考卷已出现，2021年同样“利润”类型，学生脑中应该能浮现模型解决思路，然而现实并非如此，学生忽视建模过程而望“模”却步，解答缺乏有根据的算术解答或出现直接放空等情况. 特别是在最后一问中对于题目要求“利润最大值”，部分学生通过读题得出零售数量300，利用1000-300=700得出批发数量，进而代值得出利润. 这部分学生沿袭小学解决应用题的算术解方法，细节说明不到位，还未能确立该实际问题应选用的函数模型，建立数学模型产生障碍.

（四）解题习惯不佳，反思不到位

从答题情况反馈：一是可以看出有相当一部分学生在考试中读审题时囫囵吞枣，上下文数据矛盾，一个符号或一个数字都会影响得分;二是很多学生解题步骤书写不规范，像是想起什么补什么，思路混乱;三是步步有据欠缺，学生答题重结果呈现，而不重视说理，很少反思所列式子或结果是否合理等.

思对策

方程与函数模型从小学四年级数式到六年级方程，再从七年级上册开始就不断进行演化. 可以发现，中考试题的编制绝非腾空而降，在寻找试题源头中会发现：虽“殊途”但“同归”. 中考试题大都是教材的原题或改编题，变换某一些条件或者以不同实际背景呈现，形不同，质相近. 然而学生经过多次学习和训练，都不能很好地透过现象识别本质，无法精准选择知识和解答策略进行正答，这引人深思. 那教师应如何推进数学教学环节或者学生接收知识反馈，才能有效地教与学呢？

在结合已考试题的分析和研究，从命题者角度、学生答题思维角度反观我们的数学教学，思考解决的教学对策，从而在培育核心素养下促进初中生的深度学习.

（一）激发学生学习数学兴趣

在数学学习意愿层面上，教师应关注学生兴趣的调动. 数学知识设计富有趣味性，能提高课堂的参与感和学生体验感. 教师应经常与学生交流，涵盖学习交流和情感交流，帮助学生建立学习的自信心，维持兴趣的持续性. 还要发挥自身人格魅力影响学生，正所谓“亲其师，信其道”，师生的有效交流是影响学生对数学学习评价的重要因素.

（二）培养数学运算素养

2022版的义务教育数学课标中运算能力主要指能够根据法则和运算律正确运算的能力. 2017版高中数学课标也阐明了数学运算是解决问题的素养. 二者都充分彰显数学运算的重要性，是数学的一项基本素养，被生动地称为数学中“童子功”，主要强化数学运算素养培养.

1. 明晰运算对象，确定运算方向[1]

加强算理和算法教学，让学生在学习中意识到公式法则概念等知识产生的合理性和必要性，这样形成的记忆更有章可循，具有持久性.

2. 强化学生基础计算程序记忆

学生在平时练习中遇到应用型题目时，不仅要列出式子，还要写计算过程，强化基础性运算程序的记忆;除了要教给学生正确运算程序，教师还应多板演，板书关键计算步骤，不过分追求答案准确性，规范学生运算的书写. 还可借助投影等设备有意识地展示常见错误，让学生发现错误并找到错因，订正错误，在反思总结中规避错误;收集和设计变式训练、辨析计算，在运算过程中可进行一题多解、多题一解、一题多变的训练，促进学生思维灵活性的提升和运算程序的选择优化，从而更好在试题中快速、准确地运算出正确结果.

3. 疏通运算思路节点

解题关键一环在于运算思路的正确构建. 经过长期学习，大部分学生对于很多问题会有基本思考和想法，但是随着题干条件给出方式或求解途径不同，会在答题细化上存在障碍. 因此教师在指导学生学习的时候，要注重帮助学生识别问题的类型，在关键思路障碍点给予分解，搭建脚手架帮助学生跨越障碍，精确建构运算思路和解题计划.

4. 加强“数学阅读”训练

语言文字是思维的外壳，学生阅读能力强也是其综合能力的体现. 教师在教学中应注重培养学生数学阅读能力，有意识传授学生阅读方法和技巧，从而使其阅出数学特色，读出数学语言内涵，形成正确的数学理解. 人教版教材中数学活动、阅读思考、信息技术等专题设置的有效利用，是促读促思的好素材.

那如何进行正确数学阅读呢？阅读模式大致可以这样进行：有意识引导学生在读题中有选择地提取题目关键词（信息），激活学生相关问题图式，从而做出初步的判断或假设，在进一步读题和问答中逐步完善丰满图式，寻找支撑图式的“证据”.

在阅读20题时，首先，选取熟悉的关键词——利润，激活自身储备的利润解决问题的图式，预测解题的可能情况，其中读题中强调利润问题中相关名词的含义，从而有意识进行题中数据（如40、70等数据）和预测情况中量的匹配，解决误解. 其次，有效提问，帮助学生梳理已有图式和题中数据之间的关系，修正理解. 如100、4600分别指的是零售和批发总数量和总利润，而不是其中某一个. 特别是第②小题中利润未知情况下，求零售和批发的数量，与第①小题数量、利润并没有直接关系，学生很容易搞混两次数量. 这时候教师就应适时点拨，为什么出现“最大利润”？哪一个或几个量的变化导致的？让学生结合情境再次修改和完善. 最后，越过障碍，构建清楚思路，书写过程.

（三）提高数学建模能力

数学本身就是集“数学化”与“生活化”于一身的完美的思想材料[2]. 教师应让学生获取知识的同时密切联系其相应实际背景，如此一来，既能帮助学生理解知识，增加学生的数学活动经验，还能发展学生的数学能力. 因此还原方程原始的生长点，不仅仅停留于其数学主题，还应该在教学中尝试多样化，让学生体验到数学与生活紧密联系，这样的学和教才更具有价值.