“数学分析”课程的案例库建设和案例式教学研究

［摘 要］ “十四五”规划提出，要在现代技术、未来关键技术上实现自主可控，就必须加强基础研究和人才培养，前瞻布局我国基础学科。这体现了国家对基础学科的重视，也提示了基础学科教育要为未来产业发展服务，增加对应用前景和跨专业融合等方面的引导。为此，“数学分析”课程案例式教学的改革和实践意义重大。通过联系实际应用、融入跨学科领域知识，从思维训练、知识拓展、实际应用和思政教育等方面总结案例，建立教学案例库，结合问题式学习理念设计教学过程。

［关键词］ 数学分析；案例式教学；问题式学习；课程思政

［基金项目］ 2022年度中国民航大学教育教学改革与研究项目“基于项目式教学的数学分析案例库建设与教学实践”（CAUC-2022-C2-032）；2023年度天津市高等学校本科教学质量与教学改革研究计划项目“‘课程驱动、显隐结合、多堂并举’——信息与计算科学一流专业课程思政体系建设”（B231005907）；2021年度中国民航大学国家自然科学基金配套专项“基于格林函数理论的时域声学反源问题研究”（3122022PT19）

［作者简介］ 陈 博（1990—），男，河南南阳人，数学博士，中国民航大学理学院副教授，主要从事偏微分方程反问题的数值解法研究。

［中图分类号］ G642.0 ［文献标识码］ A ［文章编号］ 1674-9324（2024）48-0123-05 ［收稿日期］ 2023-10-23

数学是从现实问题中抽象出的一门学科，但随着理论体系的建立和发展，数学只保留了现实世界中的数量关系和空间形式，舍弃其他的一切，其抽象性也逐步提高，这种抽象性在一定程度上对学生学习数学造成了阻碍［1］。传统的“数学分析”课程注重理论分析，较少涉及直观案例。众多的“数学分析”教材虽然尽量从容易认知的几何图形或者物理知识引入，但由于篇幅等因素的限制，较少涉及更为具体的案例。

通过联系实际应用、融入跨学科领域知识，建立教学案例库，结合问题式学习（problem-based learning，PBL）理念设计案例式教学过程，使“数学分析”课程更好地为人才培养服务，增加对应用前景和跨专业融合等方面的引导。

一、案例库建设

案例教学法起源于20世纪20年代，由美国哈佛商学院所倡导，该教学方法不同于传统的讲授方法，教师在课堂上的身份是设计者和激励者，带领学生主动参与课堂讨论［2］。

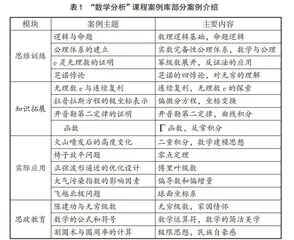
在案例式教学实行之前，首先应考虑教学案例库的建设，从思维训练、知识拓展、实际应用和思政教育等方面总结案例，丰富案例库。表1针对每一个模块给出几个案例展示。

（一）思维训练案例

在思维训练方面，主要关注案例的思考性，加深学生对概念的理解，深化学生对数学思想的认知。提升学生逻辑思维能力是“数学分析”课程的一个重要培养目标，逻辑思维能力的提高有助于学生更好地抓住事物本质，在学习的过程中更好地理解和应用课程知识，也有利于学生进行独立思考，找到问题的求解方法和思路。

以案例“逻辑与命题”为例，数理逻辑用数学方法和符号化的方式研究逻辑，其中命题逻辑关心对命题真值和复合命题的研究，涉及命题的否定“”、析取“”、合取“”、蕴含“”和等价“”等。逻辑与命题和“数学分析”课程内容息息相关，在卓里奇［3］编著的《数学分析》教材中，就把数理逻辑的内容作为开篇知识，这也体现了该内容的关键性。而在部分国内《数学分析》教材中，却将其作为大学之前的知识基础，忽略了对这一内容的介绍，这样的设定会使得部分学生在逻辑分析上缺乏思维的系统性。因此，将此案例作为思维训练案例介绍给学生是很有必要的。

数学分析中众多命题和定理都可以用数理逻辑知识进行分解分析。例如，在华东师范大学数学科学学院编写的《数学分析》上册教材中，对“数列{an}收敛于数a”的数学描述为“对任意的正数ε，存在正整数N，使得当n＞N时，有|an-a|＜ε”［4］。而其否命题“数列{an}不收敛于数a”的数学描述是一个难点，为使学生理解这一数学表述，授课时可以将原命题一段一段拆分，找出其否定描述。首先，将原命题简写为“对任意的正数ε，命题p成立”，则否定描述为“存在正数ε0，使得命题成立”；其中命题p可以写为“存在正整数N，使得命题q成立”，则命题为“对任意的正整数N，命题成立”；而命题q为“当n＞N时，有|an-a|＜ε”，则命题为“存在n＞N，使得|an-a|≥ε”。依此进行，最终得出“数列{an}不收敛于数a”的数学描述为“存在正数ε0，使得对任意的正整数N，存在n＞N，使得|an-a|≥ε”。类似的逻辑分析应用在“数学分析”课程中大量存在，虽然不完全清楚其中的数理逻辑基础也能进行学习，但良好的命题逻辑基础显然有益于对课程的理解。

（二）知识拓展案例

在知识拓展方面，结合分析学、物理学、统计学和经济学等方向相关课程，探索“数学分析”和后续课程的结合点，凝练适合课堂探讨的教学案例。“数学分析”课程是数学专业的重要专业基础课，是“微分方程”“数值分析”“概率论”“普通物理”和“经济数学”等众多课程的基础，在“数学分析”课程教学过程中，结合后续课程内容讲解知识拓展案例，有利于加深学生对本课程的理解。

以案例“无理数e与连续复利”为例，在讲解重要极限

时，可以结合经济学中的连续复利来介绍，一方面拓展学生对于经济数学的了解，另一方面也通过有趣的案例加深学生对该极限的印象。在旧社会中，借贷相关的法律法规不完善，也没有必要的监管，商人在向外借贷时，常采用高额利率和“利滚利”的方式获取高额的利息。“利滚利”即经济学中的复利，指在计算利息时，某一计息周期的利息是由本金加上先前周期所积累利息总额来计算的计息方式。假设旧社会的商人向外借贷1万元，商定年利率为100%，以复利的方式，分别以一年、一个季度、一个月和一天为计息周期，一年之后本息合计分别为多少？若按年计息，一年后本息合计（1+1）1=2万元；若按季度计息，一年后本息合计万元；若按月计息，一年后本息合计万元；若按天计息，一年后本息合计万元。可以看出，随着计息期数的增加，一年后的本息之和也对应增加。

若想使本息之和继续增加，可以进一步地缩短计息周期，增加单位时间内的计息期数。如此进行下去，当单位时间内的计息期数趋于无穷时，本息之和会如何变化？这就涉及了连续复利的概念，即在有限时间内期数趋于无限大的极限情况下对应的复利计算方式。此时，不同期之间的间隔很短，可以看作是无穷小量，也就是说，以连续复利计算，一年后应偿还的本息之和应为数列

当n趋于无穷时的极限，也就是重要极限（1）。可以证明，虽然不断增加单位时间内的计息期数会使本息之和持续增加，但其增加速度逐渐减缓，最终上述数列是有上界的。由单调有界原理可得，其值会趋向于某一极限值，此极限值即为自然对数的底数e，其值约等于2.718 28，它是一个超越数。

（三）实际应用案例

在实际应用方面，从数学分析的知识点出发，结合日常生活和工业工程等方面的实际问题，构建应用案例，鼓励学生在学习基础知识的过程中了解知识的实际应用。数学是从现实问题中抽象出的一门学科，但在发展过程中逐渐模糊了与现实问题的联系。我们希望在一定程度上呈现从现实问题到数学理论的演变过程，事实上，这种演变的过程就是数学建模。通过数学建模的思想，把实际问题和“数学分析”教学有机结合，不但能激发学生的学习兴趣，也可以启发学生用数学思维去看待世界，正如李大潜［5］所提到的，应该结合教学过程，使学生了解到他们现在所学的那些看来枯燥无味但又似乎是天经地义的概念、定理和公式，并不是无本之木、无源之水，并不是从天上掉下来的，也不是人们头脑中所固有的，而是有其现实的来源与背景，有其物理原型或表现的。

以案例“火山喷发后的高度变化”为例，在火山喷发后，大量的熔岩附着在火山上，怎么估计其高度的变化？为了将此问题数学化，需要使用数学建模的思想将实际问题化为数学问题。首先，用数学公式对火山表面的形状进行描述，假设火山表面的形状总可以用曲面

表示，其中h为火山的高度。假设火山初始高度为h0，在一次火山喷发后，有体积为V的熔岩附着在火山上，求火山喷发后的高度。

此问题的求解需要使用二重积分的知识，由火山表面的形状公式（2），火山喷发前的体积为

注意到在前述对火山表面形状的假设之下，这里火山坐落的范围并非二维空间中的有限区域，而是整个二维空间。在计算这一积分时，直接使用直角坐标系下的积分计算是无从入手的，因此，需要引入极坐标对积分进行计算。引入极坐标后，得到含有广义积分的累次积分，计算可得V0=32πh03，进而可以求得火山喷发后的高度为

这一实际案例的分析过程非常典型，当问题首次被提出时，只涉及高度、体积等数学量，看似和微积分毫无关联。然而，在分析的过程中，一旦将火山表面的形状假定为一特定曲面，所求的火山体积即为该曲面下方曲顶柱体的体积，这是二重积分的几何意义，也是二重积分建立的实际背景之一。

（四）思政教育案例

在思政教育方面，通过我国数学文化、数学之美等方面的案例，培养学生的民族自豪感以及对数学的喜爱和探索知识的动力。教育部印发的《高等学校课程思政建设指导纲要》指出，培养什么人、怎样培养人、为谁培养人是教育的根本问题，立德树人成效是检验高校一切工作的根本标准［6］。在“数学分析”课程的教学中，笔者也希望增加相关思政案例，帮助学生塑造正确的世界观、人生观和价值观。

以案例“陈建功与无穷级数”为例，陈建功是我国近代数学的奠基人之一，是我国分析数学许多分支的开拓者和学术带头人，他毕生从事数学教育和研究，在函数论等方向，特别是三角级数方面卓有成就。

陈建功从小喜欢读书，四岁时发烧，祖母不让他去上学，他却嘴里喊着“我要去的”。在杭州两级师范的高级师范求学期间，陈建功尤其喜欢数学。1913年毕业后，陈建功为了以科学富国强民，选择东渡日本深造的道路，求学期间，陈建功在三角级数方面有很多突出成就。例如，陈建功的第一篇论文《无穷乘积的若干定理》，被苏步青评价为“一篇具有重要意义的创造性著作，无论在时间上或在质量上，都标志着中国现代数学的兴起”；再如，他证明了三角级数绝对收敛的充要条件是该三角级数为杨氏连续函数的傅里叶级数，这一结果发表在日本《帝国科学院院报》上，同年，英国数学家哈代与李特尔伍德于德国《数学时报》上也发表了同一结论，这个在西方以“哈代—利特尔伍德”命名的定理，还其本源，当称为“陈—哈代—李特尔伍德定理”；此外，陈建功将著名数学家拉德马赫、孟孝夫和卡子玛茨各自对于正交函数的研究结果归结为一条基本定理，证明了它们之间是完全等价的［7］。将这些研究成果结合陈建功的人生经历介绍给学生，让学生了解早期国内学者的数学成就，也从一个侧面了解无穷级数的研究历史。

陈建功1929年在日本取得博士学位后，不留恋当时日本更好的研究条件，毅然回国投入国内教育事业，在国内函数论学派发展中做出巨大贡献。正如陈建功所说：“我来求学，是为了我的国家，也是为了家里的亲人，并非为我自己”，这样的爱国主义精神为后人树立了榜样。回国之后，陈建功来到浙江大学任教，致力于科学研究和教书育人，在浙江大学高年级学生和助教中开展数学讨论，为祖国培养了大批数学人才。即使在抗日战争期间，在敌人的轰炸中，陈建功依然坚守岗位，坚持开展研究和教学工作。九三学社评论道：“陈建功在指导青年教师和学生开展科研、培养人才、发展教育事业方面均做出了重要贡献。无论做学问，还是做人，都为后者树立了学习的榜样，人们将永记他、尊敬他。”

二、案例式教学设计

问题式学习（PBL）是一套设计学习情境的完整方法，也称作项目式教学，通常从一个需要解决的驱动问题开始进行教学，将教学分为问题提出、问题分析和问题解决三个环节，在整个讲授过程中，强调学生的自主思考能力。

案例教学的一个重要目标是培养学生思考和解决问题的能力，而PBL理念非常适合用来完成这一目标。在“数学分析”课程的教学中，这一理念的应用还需要做好细节处理。首先，单纯给出一个驱动问题的方法有利于激发学生思考的积极性和自主性，也允许学生的各种发散式思维，但“数学分析”课程对基础知识的依赖性较强，如果没有一定的知识基础，解决一个问题是很困难的。其次，一个具体问题的数学求解有其复杂性，如果不是经过长期的训练，学生很难独立地将一个复杂问题拆解为容易解决的问题。因此，除了给出驱动问题之外，还应列出可能用到的数学工具，以供学生选择。这里列出的工具不应限于某种解法所需的数学基础，而应该是所有相关知识点，这样才能不限制学生的思考，以便在讨论中碰撞出新的思想火花和方法。此外，对于较为复杂的案例，需要对问题进行逐步分解，这一分解也应该以不限制学生的独立思考为前提，考虑各种解题可能，尽量以必须解决的问题为分解问题。在详细方案中，应当尽量估计学生的思考方向，针对不同的可能性设计引导问题，目标是让学生能够尽可能地独立发现和解决问题。这样，基于PBL理念，将每一个案例当作一个项目，进行问题细化和拆分，设计出案例教学详细过程，并形成项目式教学教案。