新工科背景下高等数值分析课程教学改革的思考

摘  要：高等数值分析是数学系为理工科研究生开设的一门公共选修课程，其理论体系介于纯数学和工程应用之间，具有鲜明的特征。文章以高等数值分析课程改革为例，分析新工科背景下研究生课程教学存在的问题，针对研究生计算思维和工程思维的培养，探讨课程定位、教学内容、教学模式、考核方式、课程思政等问题。这些讨论有助于对新工科背景下研究生计算系列课程教学的现状作出一个客观评价，有助于提高计算系列课程的教学效果。

关键词：新工科建设;高等数值分析;教学模式;考核机制;课程思政

中图分类号：G642       文献标志码：A          文章编号：2096-000X（2022）24-0144-04

Abstract： Advanced Numerical Analysis is a public elective course offered by the department of Mathematics for postgraduates of science and engineering. Its theoretical system is between pure mathematics and engineering application， and has a distinct character. Taking the reform of advanced numerical analysis course as an example， this paper analyzes the problems existing in the teaching of postgraduate course under the background of new engineering education. Aiming at the cultivation of graduate students' computational thinking and engineering thinking， it discusses the course positioning， teaching content， teaching mode， evaluation mechanism， ideological and political education， etc. These discussions are helpful to make an objective evaluation of the current situation of the teaching of graduate computational courses under the background of new engineering education， and are helpful to improve the teaching effect of the series courses.

Keywords： new engineering education; Advanced Numerical Analysis; teaching mode; evaluation mechanism; the ideological and political education in all courses

一、新工科建设与高等数值分析课程

为主动应对新一轮科技革命与产业变革，支撑服务创新驱动发展、“中国制造2025”等一系列国家战略，2017年2月以来，教育部积极推进新工科建设，先后形成了“复旦共识”“天大行动”和“北京指南”，全力探索高等教育的新模式。在新工科背景下，所有能够数字化的对象都将被数字化，所有能够自动化的流程都将被自动化，海量的数据和信息极大地改变了人们的工作方式和专业技能，也使得信息处理、定量推理和数据决策成为理工科研究生应该具备的核心能力，而数值分析正是应用以上能力的数理基础。

高等数值分析是数学系为理工科研究生开设的一门公共选修课程，其理论体系介于纯数学和工程应用之间，具有鲜明的特征。从教学内容来看，该课程主要介绍计算机上常用的数值计算公式、数值方法的构造原理及适用范围，为学生使用计算机有效解决实际问题打下基础。从能力培养来看，学生通过该课程的学习将达到以下要求：（1）掌握数值分析的基本思想、基本原理和基本方法，具备利用计算机进行科学计算的能力;（2）具有运用标准算法通过编程解决实际问题的能力;（3）了解数值分析的历史、现状和最新应用情况。

二、课程教学中存在的问题

随着计算机技术的迅速发展，科学计算已成为继实验方法和理论方法之后的第三种科学研究手段，是数学及计算机实现在高科技领域应用的必不可少的纽带和工具。高等数值分析作为数学系为理工科研究生开设的一门公共选修课程，内容包括数值逼近、数值积分、求解

线性代数方程组的直接法和迭代法、非线性方程组的计算方法、矩阵特征值与特征向量的计算、最优化方法、常微分方程数值计算等，覆盖面比较广，涉及到的背景知识也比较多，是数学与计算机结合解决实际问题的重要理论支撑。

新工科建设的核心是培养适应时代发展的创新型工程科技人才，新工科背景下的课程建设强调“以学生为核心，以成果为导向”，即根据学生最终获得的能力反向推演，制订课程教学方案、教学内容和教学模式。对照上述要求，当前的高等数值分析课程教学存在如下问题。

1. 教学模式以讲授为主，学生处于被动接受状态，课堂参与度低。作为一门数学类公共基础课程，高等数值分析的教学一直面临“课程学时短、知识面跨度大、学生基础参差不齐”等问题。传统的教学模式以教师讲授为主，这种方式效率高、成本低，不受学生基础的限制，能够保证教学任务有计划、有组织地达成。然而，课堂讲授只是一种单向的知识传输方式，对于高等数值分析这样一门与工程应用和上机实践结合非常紧密的课程，单纯地讲授显得过于空泛，不能有效吸引学生的兴趣和注意力，不利于启发学生的思维和想象，难以培养学生的科学计算能力。

2. 教学内容侧重算法理论，忽视上机实践。数值分析是联系数学理论和计算机实现的纽带和工具，它有严谨而抽象的理论体系，又有很强的实践性，要求学生不仅要会数值算法理论，还要具备一定的实践应用能力。在传统的教学过程中，教师往往更加注重算法公式和理论推导，上机实践只是作为课堂教学的补充，使得教学内容偏向抽象的理论分析，忽视了上机实践与理论知识之间的联系，降低了对实践动手能力的培养和锻炼。在此模式下，学生虽然学到了算法原理和典型的数值计算方法，却很难运用到实践中去，很难独立完成算法设计。

3. 考核内容过窄，考核方式单一。传统的高等数值分析考核沿用了应试教育模式，以闭卷考试为主（占比70%）、上机实践为辅（占比30%）。试题基本来自教材和课件，由“概念-定理-例题-习题”组成。这种考核模式无法衡量学生的创新能力与实践能力，往往衍生出一种怪象，即反复刷题的学生通常会获得高分，而他们可能只会纸上谈兵，并不具备应用数学软件解决科学计算具体问题的能力。新工科背景下的课程教学高度重视“实用性”和“应用性”，科学考核学生对所学知识的掌握程度，需要对现行高等数值分析课程的考核方式进行改进。

4. 教学案例陈旧、简单，无法适应新工科人才培养的需求。新工科教育注重跨学科协同和工程思想的培养，而传统实验设计主要来自编制的数据或一些简单实际问题，从方法到方法，具有行业背景的实践教学案例十分稀少，无法锻炼学生处理实际问题的能力。

三、新工科背景下关于课程改革的几点思考

针对前述课程教学中的问题，本文就高等数值分析的课程定位、教学内容、教学模式、考核方式等问题开展如下思考，期望获得较好的教学效果。

（一）转变教学理念，重塑课程目标

传统的数学课程教学强调知识的严谨性和抽象性，忽略了数学理论的应用性，在一定程度上会带来思维定式的弊端。新工科建设要求学生的知识和技能具有宽广性、可迁移性和可持续发展性，促使我们转变教学理念，重塑高等数值分析的课程教学目标。除抽象思维和逻辑推理能力的培养之外，高等数值分析课程的教学目标还应包括计算思维和工程思维的培养。其中，计算思维是由美国卡内基梅隆大学计算机科学系主任周以真教授于2006年提出的，指运用计算机科学的基础概念进行问题求解、系统设计以及人类行为理解等涵盖计算机科学之广度的一系列思维活动。在新工科背景下，如何引导非计算机专业的学生学习、理解、掌握和应用计算思维是一个重要的问题。通过重组高等数值分析课程的教学内容，可培养学生的数学建模能力、算法设计能力和数据分析能力等，帮助非计算机专业的工科学生形成计算思维。工程思维是人类在改造自然界、构建人工自然的活动中形成的思维方式，也是新工科学生所应具备的一项核心素质。它包括解决问题所必需的工程背景知识、交流能力、批判性思维、决策能力、实践能力和创新能力等，通过设置应用教学案例、课堂研讨和课后实践等内容，可在高等数值分析课程中训练学生的工程思维。

（二）适应能力培养，重组教学内容

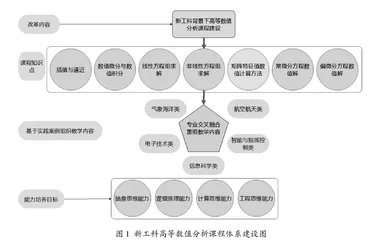
如图1所示，根据课程教学目标，重新梳理高等数值分析的理论基础及知识点的相互联系，采用“一类一例”的形式组织教学内容，突出数值分析理论与各工科专业应用的交叉融合。在开课之初，将学生按所属专业分为航空航天类、信息科学类、气象海洋类、电子技术类、智能与指挥控制类五个大类，每大类设置一个贯穿全程的实践案例。实践案例来源于实际应用问题，涉及课程的一个或多个知识点。为了引导学生了解实践目标，教师需制作相应的导学卡，内容包括案例背景、数学模型与方法、涉及到的课程知识点、测试算例和参考资料目录等。例如，对于航空航天类学生，可选取基于有限元方法的飞机机翼应力分析问题作为实践案例，该案例涉及到分片多项式插值、数值积分、大型稀疏线性方程组求解、常微分方程数值解和偏微分方程数值解等内容。这样的案例更贴近学生的专业需求，比课后习题复杂，且贯穿课程学习全过程，帮助学生将所学知识串联起来去解决一个较为复杂的工程问题，既激发了学生对本课程的学习兴趣，又能培养他们的实践动手能力。

（三）加强师生互动，创新教学模式

新工科背景下，学生成为课堂的主导，教与学的关系变得越来越微妙。考虑到研究生的培养目标之一是培养具有创新精神和从事科学研究、教学、管理或独立担负专门技术工作能力的高级专门人才，有必要在高等数值分析课堂上采用以探究式为主、其他教学法为辅的教学模式。

1. 创建民主的课堂环境。自由宽松的课堂环境容易让人的个性得到充分发挥，有利于创新意识的激发和创新能力的培养。教师与学生要建立积极的互动关系，教师不再是至高无上的权威，他与学生的关系是平等的，主要组织学生以探究的方式开展学习。为加强学生的主体意识，教师要鼓励学生积极发表意见，对于学生观点中的有效部分要善加保护和总结。

2. 按照“问题-假设-推理-验证-总结提高”的过程组织教学。探究式教学源自苏格拉底的“产婆术”，他要求教师以讨论问答的方式引导学生得出答案，而不直接教授给学生相关的知识。这种方式能发挥学生的主动性，有利于培养创新意识和创新思想。以理查森外推法的教学为例，理查森外推法是一种由低阶公式加权以提升迭代序列收敛速度的加速方法，在数值微分、数值积分以及微分方程数值解等方面都有重要应用。常规的讲法是由应用案例引入（如圆周率的计算），给出算法的思想和基本过程，用其解决案例问题，形成“从问题到理论再到问题”的教学闭环。但由于该算法构思过于巧妙，学生通常很难理解，教学效果较差。为此，可采用探究式教学法，仍从应用案例引入，首先启发学生观察计算的结果，总结出加权系数的选取规律，再进行推广，得出算法的一般思想和过程。实践证明，后一种方式更能启发学生主动思考，加深理解，把知识转化为能力。

3. 加强计算思维的培养，重视上机实践。算法若仅停留在理论推导层面无疑于纸上谈兵，产生不了任何应用价值，因此，数值实验对于高等数值分析的学习至关重要。通过综合性学习和实践性学习，使学生致力于解决现实问题，能够激发学生的学习兴趣，培养计算思维。教师在教学过程中可辅以Matlab数值实验，通过数据和图形展示算法效果，加深学生印象。按照教学计划的安排，学生需要完成一个综合性实践案例，它涉及本课程的若干知识点。在此过程中，学生需要阅读文献资料、建立数学模型、设计出合适的算法、编写计算机程序并完成测试算例，对所学知识活学活用，从中积累宝贵经验。