“会学课堂”下的数学“四会”评价例说

摘 要：聚焦学生学会学习，从“我会听、我会想、我会说、我会做”四个维度给予评价，通过“加分”或“减分”，对学生进行表扬或提醒。这就是“会学课堂”下的“四会”评价。数学课堂的“四会”评价，注重培养学生善于聆听、勤于思考、精于表达、乐于实践的习惯，帮助学生真正理解、掌握数学知识，不断提升数学核心素养。

关键词：小学数学；“会学课堂”；“四会”评价

*本文系江苏省教育科学“十四五”规划2021年度重点课题“导航成长：大数据支持下‘会学’课堂评价系统的开发与应用”（编号：B/2021/02/13）的阶段性研究成果。

聚焦学生学会学习，从“我会听、我会想、我会说、我会做”四个维度给予评价，通过“加分”或“减分”，对学生进行表扬或提醒。这就是“会学课堂”下的“四会”评价。“四会”评价不仅关注结果性评价，更注重过程性评价。与传统的评价相比，“四会”评价更多地去关注每一位学生能力素养的提升，为学生未来的成长描绘了无限可能性。本文聚焦数学学科，阐述如何依据“四会”，培养学生善于聆听、勤于思考、精于表达、乐于实践的习惯，以此推动学生个体的自我成长。

一、“我会听”维度

数学课堂的“我会听”，有以下三个基本的要义：（1）专注听。避免做小动作，不东张西望，眼睛注视着发言的同学；将别人所说和自己所想进行比较，在比较中学习。（2）听明白。首先是能听懂老师的提问和要求；接着是能听懂同学的发言并简单地判断正误，能抓住发言的重点；更高的要求是能够从几个人的不同发言中总结出共同点和不同点，听懂别人没有表达出的内容。（3）对别人的发言作出回应。通过用眼神与老师互动的方式表示自己听懂了；将自己所想和别人所说进行比较，对他人的发言作出赞同、补充、质疑、反对、综述等回应；听出数学特有表达方式的含义，快速地接受、反应、加工、总结。

【案例1】 三年级下册《年月日》练习课

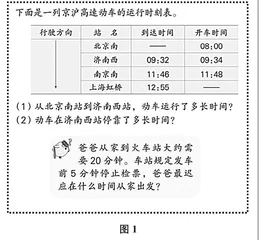
师 （出示图1）

看了这个表格，读了这个问题，你有没有发现有漏洞？或者说有不清楚的地方？

生 他从哪儿出发？到哪一站？

师 有谁能听懂他的意思？

生 爸爸在哪个地区？北京南站是8：00发车，济南西站是9：34发车。

师 也就是说，关注动车是从北京南站开出，还是从济南西站开出的。“我会听”加1分！我们不仅要认真听同学发言，还要能听懂同学的发言。

生 我知道了，还差一个条件。

师 那你能不能补一个？

生 从南京南站出发。

师 如果这时候还有同学补充发言，就加1分“我会想”。

生 规定前5分钟停止检票，南京南站是11：46到达，而发车时间是11：48，中间隔着2分钟，好像不对。

生 11：46是车到站的时间，我们应该看11：48这个发车时间，要在11：48之前5分钟到达车站，11：46是不看的。

（全班响起热烈的掌声。）

师 “我会想”“我会说”各加1分。

……

“我会听”能够帮助学生梳理和理解别人所表达的内容，在这一过程中也引发自身的思考。学生立足自身，通过“听”老师和同学的表达，发现数学中的难点，发挥乐学善学的品质，调整自己的学习状态，从而真正理解、掌握数学知识。

二、“我会想”维度

数学课堂的“我会想”，体现在以下几个方面：（1）有独立的想法。通过独立思考，有自己的想法，又有联系对比的想法。不仅如此，还可以通过倾听他人的想法，产生新思考、新想法，抑或通过对比自己和他人的想法，有新启发、新发现。（2）有疑惑地想。“会想”不一定是得出正确结果，在学习过程中产生了疑问，或是对他人的想法有不同看法，甚至质疑，也是一种“我会想”。（3）有根据、有方法地想。想法的产生不能凭空而来，而要有根据、有方法，先找到根，再顺藤摸瓜；结了一个“瓜”后，可能会根据这个“瓜”，再结第二个甚至第三个“瓜”。

【案例2】 四年级下册《运算律（练习）》

（教师出示如下习题。）

与算式“72×125”得数不相等的是（ ）

A. 9×（8×125）

B. （80-8）×125

C. 70×2×125

D. 70×125+2×125

师 你是怎么想的呢？

生 C是错的，这道题不能这样算，而要像D那样用乘法分配律。

（其他学生纷纷举手示意。）

生 A、B、C都是对的，A用的是乘法结合律，B和D用的是乘法分配律。

师 第一位同学说“C是错的”，第二位同学说了A、B、D选项的依据，你还可以分析什么？

生 我还可以分析，错误的答案错在哪里。72≠70×2，改变了计算结果。

师 真好！“我会想”加1分。还可以分析什么？

生 我可以分析A、B、D选项对的道理。A选项把72变成9×8，B选项把72变成80-8，D选项把72变成70＋2。

（全班响起热烈的掌声。）

师 真会想！“我会想”加1分。

……

【案例3】 四年级下册《整理与复习》

（教师出示一个棱长为1分米的正方体。）

师 你想到了哪些单位？

生 1平方厘米。

（学生纷纷举手示意。）

生 应该是1平方分米。

生 1平方厘米也有，只不过这个正方体的一个面上有100个1平方厘米。

师 想得很全面，“我会想”加1分。除了1平方分米，你还能想到什么单位呢？

生 还有1分米，1立方分米。

师 由1平方分米还想到了1分米和1立方分米，“我会想”加1分。那1分米应该写在哪儿？1平方分米、1立方分米呢？

生 1分米写在棱上，表示棱长;1平方分米应该写在面上，1立方分米是这个盒子的体积。

师 是的，借助纸盒对长度单位、面积单位、体积单位找到了联系。找到了联系就会思考，你还能想到什么？

生 如果一个正方体的棱长为1厘米，这个正方体一个面的面积就是1平方厘米，体积就是1立方厘米，容积就是1毫升。

师 “我会想”加1分。

……

教师第一次加分，是因为学生对产生的疑问和矛盾进行解释，发表了自己的见解。第二次、第三次加分，都是因为学生依据同学的回答再思考，顺藤摸瓜，有根据、有方法地“想”。教师的层层推进，助推学生的思维不断深入、不断进阶。

三、“我会说”维度

“我会说”是数学课堂中的重要环节，即用清晰的数学语言把数学知识、数学方法等表达出来，主要包括以下三个方面：（1）清晰说。条理清晰、简洁明了，让大家能轻松地理解自己的意思。（2）个性说。明确表达自己的见解，紧扣问题，展开论述；或就某一点深入分析，可以用示意图、线段图、算式等各种形式，自如地表达自己的想法和观点。（3）互动说。通过互评、补充等形式，在表达个体认知的同时相互学习。

【案例4】 四年级下册《运算律（练习）》

（教师出示如下习题。）

下面各题，怎样算简便就怎样算：

43×5×4 14×35 15×12

4×9×25 25×28 45×6

师 请说一说简算方法，还要说一说这种简算方法依据什么运算律。

生 25×28=25×4×7，依据乘法结合律。

师 说得真好！“我会说”加1分，给大家做了一个好榜样！

生 45×2×（6÷2）。

师 如果你会听、会想，就一定知道怎么说。

生 （再次说）

45×2×3，依据乘法结合律。

（掌声响起。）

师 （询问全体学生）

这回能不能给他加1分“我会说”？

生 可以。

……

【案例5】 四年级下册《解决问题的策略》

（教师出示图2，这是学生出的一道习题。教师引导学生画出图3来理解题意，有一个学生举手，表示他有新的想法，如图4。）

生 我用一个正方形表示赔偿的98千克米，一半是牛吃的，马吃的是牛的一半，羊又吃了剩下的一半，就相当于把这个正方形平均分成8份，一共吃了7份。

（学生陆续举手。）

生 我觉得他画的这个图不太清楚，还是刚才的线段图比较清楚。

生 也可以呀，但要把里面也分一分，才看得清楚。

师 你说一说，我来画。

生 要看出羊吃了一份，马吃了两份，牛吃了四份。

（师生合作，画出了图5。）

师 所以，并不是被分成8份的正方形表示98千克，而是被分成7份的缺角“正方形”表示98千克。两位同学“我会说”各加1分。

……

案例4中，教师不断引导、指导学生如何“清晰说”。这里的“说”，还需依据“听”，认真“想”，照样子“说”。案例5中，第一位学生依据示意图发表自己的见解与看法，其他学生积极主动地进行互评和补充发言，在该生的“初等图”上进一步挖掘、改善，是课堂上学生“个性说”“互相说”的生动体现。

四、“我会做”维度

“我会做”不仅要动手，还要动眼、动脑。从这个意义上来看，首先要“会听”“会想”，才能“会做”。数学课堂的“我会做”，主要体现在以下几个方面：（1）自主做。按照老师或题目要求，自主探索实践，独立完成任务。（2）会合作。在无法独立完成时，和同学合作完成;主动帮助有需要的同学一起完成。（3）有创造。对操作过程与结果进行反思、归纳，对自己的原先做法进行优化，富有创造性。

【案例6】 六年级下册《解决问题的策略》

课前，教师让学生用不同的解法尝试解决教材上的例题：“星河小学美术组男生人数占总人数的2/5。已知女生有21人，男生有多少人？”

课上，教师请一组学生到讲台前汇报。小组4名学生依次边板书边汇报解法。他们有序地板书，清晰地讲解思路;组长在其他组员讲解时帮助圈画关键词，板书重点内容。最后的板书如图6所示。

小组汇报完毕，其他学生进行补充，一道题一共写了7种解法。一节课有15分钟时间，是这个小组的学生带领全班充分地交流、探究，进一步积累分析数量关系的经验，体会画图、转化等策略在解决问题过程中的作用。这一组的每位学生都加1分“我会做”。

……

【案例7】 四年级下册《解决问题的策略》

（教师出示如下习题。）

航模组有男生8人、女生6人，美术组的人数是航模组的2倍，合唱组有84人，合唱组的人数是美术组的几倍？

师 （出示两位学生的两种算法，如图7）

两种算法，有联系吗？

生 其实是一样的，这里运用到除法的性质，a÷（b×c）=a÷b÷c。

师 我请两位同学同步指一指这两种算法的计算过程，（在图7中添加了字母公式）

你能从下面字母公式中找到吗？

（两位学生上台同步指，如图8。）

师 两位同学各加1分“我会做”。

……

当然，“四会”评价中的“四会”不是独立割裂的四个维度，而是相互勾连、融会贯通的一个整体：“会听”是基础，“会听”才能做到“会想”“会说”“会做”；“会说”“会做”又是“会想”的输出和表达，是“会学”的关键，也是“会学”的最终体现。“会学课堂”，让“听、想、说、做”互促共进，助力学生不断“生长”。