“双减”背景下高中数学课堂教学设计案例
作者: 谭忠念
“双减”政策是国家对教育模式的重大调整,更是教育观念的大变革。在此背景下,改变课堂教学模式、提高教学效率,真正实现减负增效。要想提高课堂的教学效率,必须进行有效地课堂教学情境设计,使课堂教学实效化。教师需要对教学过程进行预判,利用先进的教学理念,创新教学方式,适应时代的潮流,对课堂教学进行改进和优化。结合高中数学教学,特设计如下教学案例,供大家参考。
§3.2.1函数的单调性(人教A版)
教学目的:(1)通过已学过的函数特别是二次函数,理解函数的单调性及其几何意义;
(2)学会运用函数图象理解和研究函数的性质;
(3)能够熟练应用定义判断函数在某区间上的的单调性.
教学重点:函数的单调性及其几何意义.
教学难点:利用函数的单调性定义判断或证明函数的单调性.
教学思路:
一、 创设情景,引入课题
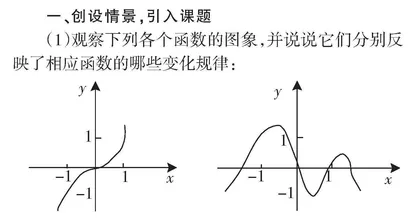
(1)观察下列各个函数的图象,并说说它们分别反映了相应函数的哪些变化规律:
1 随x的增大,y的值有什么变化?
2 能否看出函数的最大、最小值?
3 函数图象是否具有某种对称性?
(2)画出下列函数的图象,观察其变化规律:
1.f(x) = x
1 从左至右图象上升还是下降 ______?
2 在区间 ____________ 上,随着x的增
大,f(x)的值随着 ________ .
2.f(x) = -2x+1
1 从左至右图象上升还是下降 ______?
2 在区间 ____________ 上,随着x的增
大,f(x)的值随着 ________ .
3.f(x) = x2
1在区间 ____________ 上,f(x)的值随
着x的增大而 ________ .
2 在区间 ____________ 上,f(x)的值随
着x的增大而 ________ .
二:研探新知
(一)函数单调性定义
1.增函数
一般地,设函数y=f(x)的定义域为D,
如果对于定义域D内的某个区间I内的任意两个自变量x1,x2,当x1<x2时,都有f(x1)<f(x2),那么就说f(x)在区间I上是增函数(increasing function).
思考:仿照增函数的定义说出减函数的定义.(学生活动)
注意:
1 函数的单调性是在定义域内的某个区间上的性质,是函数的局部性质;
2 必须是对于区间I内的任意两个自变量x1,x2;当x1<x2时,总有f(x1)<f(x2) .
2.函数的单调性定义
如果函数y=f(x)在某个区间上是增函数或是减函数,那么就说函数y=f(x)在这一区间具有(严格的)单调性,区间I叫做y=f(x)的单调区间:
3.判断函数单调性的方法步骤
利用定义证明函数f(x)在给定的区间I上的单调性的一般步骤:
1 任取x1,x2∈I,且x1<x2;
2 作差f(x1)-f(x2);
3 变形(通常是因式分解和配方);
4 定号(即判断差f(x1)-f(x2)的正负);
5 下结论(即指出函数f(x)在给定的区间D上的单调性).
(二)典型例题
例1.(教材P76图3.2-1)根据函数图象说明函数的单调性.
解:(略)
巩固练习:课本P85习题第1题
例2.(教材P78例1)根据函数单调性定义证明函数的单调性.
解:(略)
巩固练习:
1 课本P79练习第2、3题;
2 证明函数 在(1,+∞)上为增函数.
例3.借助计算机作出函数y =-x2 +2 | x | + 3的图象并指出它的的单调区间.
解:(略)
思考:画出反比例函数 的图象.
1 这个函数的定义域D是什么?
2 它在定义域D上的单调性怎样?证明你的结论.
说明:本例可利用几何画板、函数图象生成课件等作出函数图象.
三:归纳小结,强化思想
函数的单调性一般是先根据图象判断,再利用定义证明.画函数图象通常借助多媒体,求函数的单调区间时必须要注意函数的定义域,单调性的证明一般分五步:
取 值 → 作 差 → 变 形 → 定 号 → 下结论
四:作业布置
1. 书面作业:课本P86 习题3.2 第2- 4题.
2. 提高作业:设f(x)是定义在R上的增函数,f(xy)=f(x)+f(y),
1 求f(0)、f(1)的值;
2 若f(3)=1,求不等式f(x)+f(x-2)>1的解集.
课堂是实施有效教学的主阵地,“双减”对我们的课堂教学提出了更高的要求,教师正面临着新的挑战和机遇,只有提高课堂教学效率,才能把教师从繁忙的教学工作解脱出来,把学生从繁重的学习任务中解放出来,全面提高学生的综合素质,真正实现“双减”提出的培养目标。