渐进演化：算法教学的路径与关键策略

摘要：本文针对义务教育阶段信息科技课程中的算法教学，提出将算法逻辑与学生认知逻辑结合，构建“明确基本逻辑—抽象与建模—算法设计—验证与优化”的路径，并在此基础上应用“以简为始”“具体—抽象”“化错而解”等关键策略，进而有效提高算法教学效率。

关键词：算法教学；学习逻辑；教学路径；策略

中图分类号：G434  文献标识码：A  论文编号：1674-2117（2025）06-0019-04

算法是信息科技解决问题的关键要素，它在信息科技课程中的重要性毋庸置疑。《义务教育信息科技课程标准（2022年版）》（以下简称“新课标”）将“身边的算法”模块设置在5～6年级作为起步，已充分考虑到了该年龄段的学生“由具象至抽象过渡”的思维特点。然而，算法仍成为一线教师普遍认为的“最难啃”的内容。具体困扰教师的问题是：“知道要让学生理解算法，但很难找到一条让学生较容易理解的路”，课堂经常表现为“很枯燥”“无趣”“时间来不及”“学生难以理解”“两极分化严重”等。据笔者观察，其症结主要在于教学缺少将算法逻辑转化为学生认知逻辑的方法。鉴于此，笔者尝试以“渐进演化”为主题，探讨初学算法的教学路径与关键策略。

算法教学的困境归因

1.对“问题解决逻辑”的理解缺乏重视

对于算法教学，要凸显“抽象与建模”已成为教师的共识。然而，这种共识逐渐变成一种过度重视，从而导致“抽象与建模”前思考环节被忽视，即缺乏对问题本身的分析及对问题解决的基本逻辑的思考。

2.“抽象—建模—算法”进阶层次不明

很多教师意识到“抽象—建模—算法”这三个环节是进阶的，但不清楚前者与后者的具体关系。例如，没有认识到“建模实质是在构造算法的核心，建模在增补‘输入’‘输出’‘控制结构’等要素后，即可刻画出完整的算法设计”。

3.重视程序实现而忽视算法解读与验证

部分教师认为“程序能跑起来”便是算法构建的“终点”，没有意识到“代码解读”“测试验证”等活动乃是算法构建的闭环，因此存在学生探究路程短、自主思考深度不够等问题。

算法教学的“渐进演化”路径

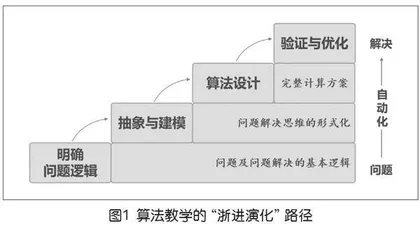
针对上述问题，笔者提出构建“渐进演化”的算法教学思路，即将“算法建构”这个大问题分解为多个小问题，并以“自动化”为目标，对问题求解设计进行逐层抽象与演进，促进学生的算法学习（如上页图1）。

1.明确问题逻辑

“明确问题逻辑”也就是要知道所求的问题是什么，该问题如何求解。这里的“求解”是重在明确“人”解决问题的基本思路，而不是急于思考“计算机”如何求解，即让学生优先明白“问题与问题求解是怎么一回事”。例如，在《算法与问题解决》一课中，针对“投票”情境，首先让学生把握“投票”考虑的是计票问题，投给哪个作品编号，对应作品就增加票数。如果学生把问题求解的基本逻辑“想清楚了”，那么后续的抽象与建模，就能自主进行算法建构。

2.抽象与建模

抽象可以是计算框架的抽象，也可以是数据变量的抽象，还可以是关键对象间关系的抽象。例如，以“输入—计算—输出”三环节来解构“投票”问题，就是一种抽象思考；用变量tp存储输入的作品编号，用变量a表示a作品的计票数，用变量b表示b作品的计票数，就是对数据的抽象；而输入的编号需经过判断计入对应作品的票数，是为关键对象间关系的抽象。在抽象基础上，即可建模，也就是确定“怎么算”。

3.算法设计

算法设计就是在建模的基础上，通过增加输入、输出及控制结构等部分，使整个计算过程的步骤既明确又完整，且确保算法的确定性、可行性和有穷性。从严格意义上来讲，抽象与建模早已涉及算法设计。因此，这里的“算法设计”环节更强调的是可执行的完整性，如“投票何时终止”“哪些变量需要初始化”等这些细节问题，都应在完整的算法设计中被考虑。

值得注意的是，如果算法起初是用自然语言、流程图或伪代码描述的，那么就需要通过编程，将算法转换为某编程语言特定的语法、函数名及结构。

4.验证与优化

验证环节主要通过输入不同的数据，观察程序的运行与结果，验证算法的正确性、健壮性及效率。通过编程，学生感受到算法自动化解决问题的魅力；通过验证，学生切身感受程序运作的机制，理解用抽象代码所表达的计算过程，同时进一步发现问题，以“优化”行动促进学习的深化。例如，通过输入交替的作品编号“01、23、01”，输入不是原定的编号“28”来考验程序，发现并修正算法设计中的BUG。

算法教学的关键策略

1.“以简为始”策略

“以简为始”策略遵循“从简单入手”，即将问题求解的算法从复杂结构降维成简单结构，满足最基本的问题求解的需求，在学生能自主构建后，再提出新的问题或更高的需求，引发算法优化与升级，为学生铺设一种由简单至复杂的算法探究之路。

在实际教学中，教师可以反向操作，以终至始地“化繁为简”，如图2所示。具体来说可分以下步骤：①根据问题情境，先设计出较为完备的算法，并将算法付诸代码，得到程序P；②针对问题求解的基本需求，剔除程序的非关键部分，但使程序仍保持求解问题的基本功能，得到程序P’；③分析“程序P”至“程序P’”之间的差距，设计出学习进阶环节，能胜任的部分让全体学生“做中学”，不能胜任的部分，可以通过分层教学或师生演示，让学生“观中拓”。

以案例“投票算法‘变形记’”为例，在“投票算法”备课中，笔者发现，一个完备的作品投票算法，应具备的功能为支持多项作品、投票作品编号可自定义、能自动计票、可随时退出程序。若一开始就要学生思考实现所有功能的算法，则既会陡然增加学习的难度，也不太可能让学生在四十分钟内完成。因此，笔者将问题情境做了三处简化处理：一是仅给两件作品投票，编号确定为“01”和“23”；二是循环模拟与退出程序功能不要求学生构建，仅让学生有所了解；三是建模让学生动手实践，但程序不要求学生从零起点编写，只要求完成计票的关键代码。经过一番简化，学生人人都能“上手”，课堂气氛活跃，学生自我成就感明显。在“程序跑起来”后，学生输入“28”编号加以验证，发现“投01之外的编号，都会计票在b作品”的算法漏洞，自然引发算法优化。在课堂最后，教师让学生访问网页，对本课收获感进行投票，切身感受“更真实”的投票程序，感受基于网络的“并发式”自动计票的魅力。

2.“具体—抽象”策略

“具体—抽象”策略关注的是两者的联结与互为依赖的渐进迭代。从具体至抽象，是一种建构，符合学生的认知规律；从抽象至具体，是一种解构，往往指解读代码、验证算法等思考与实践。这些活动能评价学生对抽象算法的理解，促进计算思维的提升。

在实际教学活动，“具体—抽象”交织着推进深度学习（如图3）：①从具体入手，以具体数据计算为切入口，理解问题求解的基本逻辑；②从具体至抽象，由于“任何概念、问题或知识，都可以用一种极其简单的形式来表示”，因而教师可借助具体例子，配以简明图示，揭示对象间的关系，在理解的基础上，学生完全能自我发现并描述计算的规则；③从抽象至抽象，用代码将算法变现为程序；④从抽象至具体，让程序“跑起来”，眼见为实地看到程序运行的过程与结果，感受计算的自动化；⑤从具体至抽象，将程序运行结果与代码互为对照，逐行解读代码“做什么”，针对错误寻觅“为什么”，促进理解的深化与新一轮建构的行动。

以案例“投票算法的抽象改良”为例，在“投票”算法教学中，笔者发现，不管学生基础如何，大部分学生都会在变量抽象和形式化描述处“卡壳”。究其原因是，学生尚未清楚“如何计票”，教师就“祭出”变量并设计算法，所以相当茫然。在后来的教学中，笔者让教学慢下来，让学生先明白“输入哪个编号，计票计在哪里”，即先厘清“问题解决的基本逻辑”，在此基础上设定变量，描述计票规则，自然演进至算法设计，关键教学片段如上页表所示。

3.“化错而解”策略

在算法实践的过程中，错误是不可避免的，错误可能出自建模的缺陷，也可能产生于程序语法的不合规范。一般来说，“化错”可遵循以下的过程：①收集典型错误，视算法错误现象为常态，视错误为学习的契机，甚至感谢错误案例的提供者，在课堂中创设安全的学习氛围；②聚焦错误点，重现程序运行的错误现场，先看清楚“错什么”，借助具体代入法、逐行分析法，引导学生察觉“错在哪里”，理解“为什么出错”；③修正算法错误，引导学生还原问题解决的基本思路，对模型、代码进行修正；④验证修正后的算法，这一步仍不可少，再次验证也凸显了严谨、务实的科学态度。

例如，在五上《双分支结构》算法教学中，教师创设购物打折情境，为学生提供“三步”支架，引导学生在PPT中用自然语言构建算法。

在课堂上，一位学生很快地写出“打折判断的条件——是否大于5”，紧接着，在“付款费用”一栏中，写下了令笔者非常疑惑的表达式“n-（n/1）”。这肯定是错了，这位学生逻辑思维有问题。笔者询问该生：“你是怎样想的？”学生回答：“因为原价是10元，打折是9元，每条少1元……”笔者根据回答意识到，该生计算逻辑没错，仅是形式化转化上出错。然后，笔者让该生以“购买6条”为例，具体代入表达式试一试，他立马意识到“忘记了将数量与价格相乘”，很快将表达式修正为n*10-（n*1）。

综上所述，“渐进演化”本身也可以视作一种因学而定、分而治之的教学算法，它构造了一种逐层进阶的算法学习路径，能促进算法理解，提升学生的学习成就感。置身于有意义的问题情境，在抽象与建模的浸润中，触摸程序的诞生与优化，通过“做”与“悟”，让每一个学习者都能真切地感受到，人可以形式化地表征问题解决的思维，而“形式化”可转换为“自动化”，这就是算法教学中的深邃而又迷人的魅力。

参考文献：

[1]钟启泉.深度学习[M].上海：华东师范大学出版社，2021：16.

[2]布鲁纳.布鲁纳教育论著选[M].邵瑞珍，张渭城，译.北京：人民教育出版社，2018：129+183.

作者简介：费海明，浙江省宁波市江北区教育局教研室信息科技教研员，正高级教师，曾获全国信息科技优质课特等奖，宁波市拔尖人才，浙江省优秀教研员，人教社信息科技教学指南编者，浙江省信息科技学科评价专家，浙江师范大学兼职教授。