再生冷却通道内超临界流动中的布雷斯悖论研究

摘 要：      基于碳氢燃料的再生冷却系统是突破超燃冲压发动机长时间可靠运行的关键， 加工误差可能导致的局部连通会改变系统流量分配， 进而容易造成结构破坏。 现有研究发现特定工况下微型网络通道内会发生流动的布雷斯悖论现象， 即通道网络局部连通时系统流量反而低于不连通情况。 本文重点探究宏观尺度条件下局部连接通道网络内是否会发生布雷斯悖论， 关注该现象发生的条件及影响因素， 研究系统流量变化对热防护系统换热特性的影响。 首先基于数值模拟方法， 证明了布雷斯悖论现象的存在， 即特定工况下连接通道开启状态的H型通道总流量反而小于连接通道关闭状态下的总流量。 然后考虑障碍物位置、 大小、 连通位置以及宽度等因素， 对比分析了仿真结果与平行冷却通道的系统流量大小， 在此基础上总结了布雷斯悖论现象发生的规律。

关键词：     再生冷却通道； 布雷斯悖论； 超临界流体； 对流换热

中图分类号：      TJ760； V231

文献标识码：    A

文章编号：     1673-5048（2025）01-0090-09

DOI： 10.12132/ISSN.1673-5048.2024.0194

0 引  言

作为一种典型吸气式动力系统， 超燃冲压发动机能够捕获外部气流作为氧化剂， 比冲性能明显高于传统的液体火箭发动机， 研制超燃冲压发动机对高超声速推进技术发展意义重大。

高马赫数飞行模式下进气道捕获气流总焓很高， 同时与燃料发生化学反应释放大量热， 发动机本体结构面临极端的热环境。 为了防止高温烧蚀以及结构热变形， 必须采取有效的发动机结构热防护方案。 根据换热方式的不同， 发动机结构热防护主要分为主动冷却和被动热防护两大类， 其中基于碳氢燃料的再生冷却技术应用最为成熟。

目前有许多学者开展了关于再生冷却通道内对流换热机理的研究， 大量学者倾向于借助数值模拟方法研究超临界条件下燃料的对流换热现象^［1-3］， 也有部分学者基于动力学模型进行热解实验， 将实验获得的数据与相关数据进行比较， 预测再生冷却通道燃料的热解机理^［4-5］。 在超临界压力下燃料物性参数随温度剧烈变化， 热流密度会导致冷却剂传热系数下降， 进而导致传热恶化现象。 Li等^［6］分别运用k-ω SST模型和k-ε模型模拟超临界正癸烷湍流向上和向下的两种流动传热情况， 开展对再生冷却通道内传热恶化机理的研究， 以最大程度减少热防护带来的损失为目的。 一些学者开展了再生冷却通道的结构设计优化， 相继提出了新型方案以增强再生冷却通道的传热性能^［7-8］。 为了探究热防护的机理， 冉振华等^［9］开始研究并联通道内部的流量分配特性， 以准确预测流体的动态运输和流动行为。

布雷斯悖论是博弈论和网络相结合的经典悖论， 新建道路可能反而加剧拥堵， 增大交通路网的路容量反而会造成出行时间延长， 降低整条交通网络某一时刻的车流量。 针对特定交通路网的研究发现， 在低交通需求和高需求下不发生布雷斯悖论， 在中间需求区间内才可能发生布雷斯悖论^［10］。 对于自然科学领域， 近年一些学者也探讨了布雷斯悖论作用于电网、 通信网络、 微流体管道中的机理。 Case等^［11］利用OpenFOAM进行数值仿真， 结合实验获得的数据， 验证布雷斯悖论支持流体模拟， 通过模拟在施加压力和流速之间呈现非线性关系的微流体网络来解决微流体系统集成控制机制的难题。

再生冷却系统由一系列微型通道组成， 可通过传统机械手段或3D打印增材制造等技术制造。 考虑串腔这种极端情况， 冷却通道内超临界流动状态与交通网络原理极为类似， 在某一流量范围内也可能出现布雷斯悖论现象， 进而影响发动机再生冷却系统的对流换热过程， 因此开展超临界流动的布雷斯悖论具有重要研究价值。

1 物理模型与数值方法

1.1 模型建立

已有研究证明， 微流体网络中的不可压流动存在布雷斯悖论现象^［11］。 并且设计了H型的流体通道结构， 如图1所示。

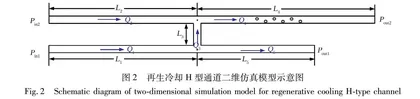
发动机再生冷却系统由薄壁金属夹层结构组成， 内部包含一系列小尺度通道。 基于文献［11］， 建立并联再生冷却通道简化的物理模型， 图1所示的微流体通道模型的尺寸为500 μm×500 μm ， 相较于实际再生冷却通道尺度量级过小。 为了研究宏观尺度流动网络内的流动特征， 重新选取5 mm×5 mm截面尺寸的计算区域， 采用H型并联通道开展仿真分析， 只是在原有尺度比例上进行微小调整。 考虑到再生冷却通道入口并联排列， 将两个入口Inlet1和Inlet2设置在同一截面位置， 将工质由水修改为煤油。 为了保证流动压降与流量的非均匀性， 在上面的流动分支内设置了6个障碍物， 中间通道连接模拟加工误差造成的流道串联现象， 详细模型如图2所示。

为了进一步分析H型通道结构调整会对通道内部流体流动状态产生影响， 基于控制变量原则， 考虑改变障碍物间距、 障碍物与壁面之间距离、 障碍物大小、 连接通道宽度、 连接位置等参数， 分别构建5种障碍物通道段的物理模型以及6种典型的H型通道物理模型， 具体的尺寸参数如表1～2所示。

完成对H型通道的二维仿真模拟， 考虑壁面热流边界条件， 进行H型通道的三维仿真， 构建三维工况模型， 如图3所示。

导入编译好的煤油物性udf， 煤油超临界热物性经过了详细的验证过程， 在3 MPa下， 航空煤油热物性计算结果与实验值^［12-15］对比如图4所示。 分析发现， 该模型能较好地反映航空煤油热物性的变化， 计算结果与实验值之间的平均误差小于10%。

施加不同的壁面热流边界条件， 分别将热流密度设置为0 W/m2， 500 W/m2， 10 000 W/m2， 100 000 W/m2。

1.2 通道流量的计算

由图1可知， H型通道分为L1， L2， L3， L4， L5共5段， 其中， 障碍物通道L4有不规则分布的圆柱形障碍物， 目的是保持通道L4流量与压降之间的非线性关系。 为了计算流体网络在稳态下系统的总流量， 需要根据相关理论获得各段通道出入口之间的压降， 根据压降与流量之间的关系方程进行换算， 获得各段通道的流量。 在本文的H型通道模型中， 通道类型主要可以分为无障碍物的通道与有障碍物的通道两类， 对于不同类型的通道， 通道的流量与压降之间的关系方程不同。

对于无障碍物通道段， 采用改变出入口压降控制通道流动状态的方式， 对通道的流量进行调节。 可以采用两种入口压力控制方式， 分别是入口静压控制与入口总压控制。 通道的出口统一设置为出口静压为0 Pa。 通道的长度为L， 宽度为w， 在近似二维泊肃叶流动情况下， 对于Lw 的无障碍物通道， 二维Navier-Stokes方程的近似稳态解表明单位深度的总体积流量Q与沿流道的压降ΔP之间存在线性关系：

Q=－ΔPw312μL（1）

而在三维模拟的情况下， 通道的速度表达式可以近似为V=Q/（wh）， 其中， h为通道的截面高度， 无障碍物通道的压降与流量之间的关系方程为

Q=－ΔPw3h12μL（2）

对于有障碍物通道段， 不同于无障碍物通道内部出入口压降与流量之间呈线性关系， 存在障碍物时通道内部两者之间是非线性的。 考虑存在障碍物通道内的流动近似符合多孔介质假设， 因此管内流动遵循达西定律。 当压力梯度或者流速较小时， 流动速度与压力梯度之间存在线性关系； 当流动雷诺数增大到一定程度时， 压降与流量之间呈现非线性关系， Forchheimer提出了经验公式来分析这种流动状态^［16］：

ΔP=αV+βV2（3）

式中： V为流体平均速度； α为互易渗透率； β为非达西流动系数， β与通道的孔隙大小、 形状、 孔隙率有关。

对于非达西流动， 采用雷诺数Re作为判别准则。 雷诺数可以表示为惯性力与粘性力的比值， Re=ρUL0/μ， 其中， L0为通道的水力直径， 作为系统的特征长度可以用4A/P来表示， A为通道横截面积， P为周长。 在二维和三维的情况下， 通道的水力直径分别为2w和2wh/（w+h）， h为三维情况下， 通道横截面的高度。 因此， 在二维和三维情况下， 通道的特征速度分别是Q/w和Q/（wh）。 雷诺数与流量之间的关系式分别为Re=2ρQ/μ 与Re=2ρQ/μ（w+h）。 多孔介质的流动可以分为三种， 即线性达西流动、 立方过渡流动和二次Forchheimer流动， 对于本文提出的有障碍物通道流动， 适用于Forchheimer方程。 转化为通道出入口压降与流量之间的非线性关系， 方程的具体表示式如下：

－ΔP=αμ2L2ρwRe+βμ2L4ρw2Re2 （4）

式中： α与β分别是通道系统的互易渗透率和非达西流动系数， 都只和障碍物通道几何构型有关。

验证布雷斯悖论需要通过障碍物通道的模拟获得该通道所对应的互易渗透率α和非达西流量系数β， 两者都完全取决于含障碍物通道系统的几何形状。 已知H型通道两个入口和两个出口的压力边界条件， 根据沿通道压力守恒方程和流量守恒方程可以获得如下的方程组：

Pin－P1=12μL1w3Q1（5）

Pin－P2=12μL1w3Q2（6）

P2－PoutL4=αμwQ4+βμw2Q24（7）

Q3+Q2－Q4=0（8）

Q3+Q5－Q1=0（9）

根据方程组可获得两个出口段的流量、 出口段的流量之和近似为H型通道的总流量。

1.3 数值方法验证

仿真模拟利用压力基求解器， 管内流动选择k-ε SST模型， 压力耦合算法选择Simple算法。 雷诺数与速度之间存在V=Reμ/（ρL） 的线性关系， 入口边界设置为速度入口条件， 出口边界条件统一设置为0 Pa， 环境压强设置为0 Pa， 通道内部流体工质为水， 物性参数从数据库中选择。

为了验证仿真方法的可靠性， 首先进行网格无关性检验。 针对同一模型划分不同分辨率的网格， 网格量分别为40万、 120万和180万。 计算过程中模型的选取完全一致， 控制边界条件相同。 以入口静压为控制变量， 利用已有的理论基础计算H型通道总流量， 仿真结果如图5所示。

由图5可知， 在40万、 120万、 180万的网格尺度下H型流道的仿真结果差异较小。 为了保证仿真结果的可靠性， 并且减少计算消耗的资源， 采取120万的网格开展仿真分析。

选取文献［11］的微流体通道仿真案例， 构建相同的模型进行仿真模拟， 设置入口静压边界条件在100～2 000 Pa范围内变化的10组工况， 提取H型通道开闭状态下P1， P2点处的静压数据。 将文献［11］的结果与本文的仿真后处理数据进行比较， 如图6所示。