数学界的谜题

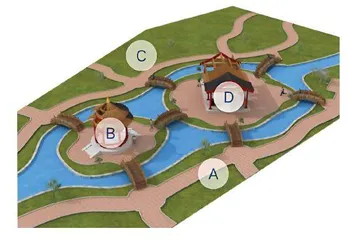
在北京科学中心的户外空间有7座中国古建风格的木桥，它们共同还原了一个载入史册的科学问题，这要追溯到千里之外的加里宁格勒……

加里宁格勒州是俄罗斯最小的州，中心城市是加里宁格勒，原名哥尼斯堡（K nigsberg）。它位于俄罗斯最西边，南邻波兰，东北部和东部与立陶宛接壤，领土多为低平原。境内主要的河流有涅曼河——115公里，普列戈利亚河——123公里，还分布着100多个大大小小的湖泊及若干沼泽。

18世纪的哥尼斯堡是东普鲁士的贸易与军事重镇，桥梁则是市民通勤、商人运货、士兵调动的必经之路。普列戈利亚河将城市分割为4块陆地：两个河心岛与两岸的旧城、新城，7座桥梁横跨河流，成为连接城市生活的纽带。市民们每日穿行于这些桥梁之间，逐渐萌生了一个看似简单却困扰众人的疑问：“能否不重复、不遗漏地一次走遍所有7座桥，最终回到起点？” 尽管无数人尝试，却始终找不到解法，这一谜题逐渐成为数学界的焦点——哥尼斯堡七桥问题。

1736年，天才数学家欧拉（Leonhard Euler）受此问题启发，摒弃传统的试错法，转而用抽象思维将其转化为一个几何问题。他将4块陆地抽象为点（两岸为A、C点，两座岛为B、D点），7座桥抽象为线，构建了一个图论模型。如此一来，七桥问题就变成了“以下图形能否一笔画完”的问题：

欧拉发现，一个图形能否一笔画完的关键，在于连接每个点的线有多少条：如果每个点上连接的线都是偶数条（如2条、4条、6条），那么可以一笔画完，并且返回起点；如果有且只有2个点上连接的线是奇数条（如1条、3条、5条），那也可以一笔画完。如果一笔画起点上的线为奇数条，那么终点上的线也为奇数条；如果只有1个点或者超过2个点连接的线是奇数条，就无法一笔画完。

在七桥问题中，与4个点连接的线数量分别是：A点3条（奇数），B点3条（奇数），C点3条（奇数），D点5条（奇数），欧拉由此得出结论：七桥问题无解。另有人提出，可通过增加1座桥来解决七桥问题。你知道这座桥应该如何建吗？为何多建1座桥能解决问题？

1736年29岁的欧拉向圣彼得堡科学院递交了《哥尼斯堡的七座桥》的论文，开创了数学的一个新的分支——图论与几何拓扑。他将实际问题抽象为“点—线”结构的思想成为图论的基础，后应用于网络分析、交通规划、社交网络等领域；而他提出的“几何位置”（geometry situs）概念，强调物体间的位置关系而非它们的形状和大小，成为拓扑学的前身，著名的欧拉公式也源于此。

如果你来到俄罗斯加里宁格勒，想一次性打卡七桥问题中的七座桥是不可能的。不仅因为那道无解的命题，更因战火硝烟与河流变迁早已抹去了它们的痕迹，但七桥问题作为宝贵的科学遗产，在数学史上仍熠熠生辉。