数学结构化教学中教学主线的价值及设计路径

摘 要 教学主线是指教学时所依托的主要思路或重要线索，在教学活动中起着统领、协调、推进教学活动的作用，它是结构化学习观、学科观与课程观的具体体现。教学主线是数学结构化教学的经脉，是落实新课标结构化设计理念的重要路径：一方面，借助教学主线“生长点、关联线、逻辑面、教学块”的设计，让内容开发有了设计流程，解决“教什么”的问题；另一方面，借助教学主线“板块化”的呈现，让活动开展有了实施路径，解决“怎么教”的问题。

关  键  词 小学教学 结构化教学 教学主线

引用格式 王卫东.数学结构化教学中教学主线的价值及设计路径[J].教学与管理，2023（08）：48-52.

“形散而神不散”是散文的写作手法，所谓的“形散”是指散文的取材比较广泛，不受时间与空间的限制，表现方法不拘一格，而“神不散”是指散文中要表述的中心思想明确而集中。这种写作手法与数学教学方法也存在相通之处：数学教学中的“形散”体现在教学内容丰富、教学方式多样，而“神不散”则体现在教学活动过程中，借助一条教学主线，将众多教学内容进行取舍、串联、融合，进而使得课堂教学形成一个有机的整体。

教学主线就是“形散而神不散”中的“神”。它是教学活动所依托的主要教学思路或重要教学线索，在教学过程中发挥着统领、协调、推进整个教学活动的作用。教学主线是数学结构化教学的经脉，是落实新课标结构化设计理念的重要路径，下面笔者就教学主线在结构化教学中的价值、设计与实施谈谈自己的实践与思考。

一、教学主线的价值追寻

教学主线是数学结构化教学的外化表现形式之一，其价值主要体现在以下三个方面。

1.教学主线是结构化学习观的体现

心理学研究者通过对比实验发现，结构化对知识学习具有重要作用，当知识以一种结构化的方式进行储存时，便可以大大提高知识应用时的检索效率。因此，不管是知识的呈现方式，还是数学的学习过程，都离不开结构化的设计与实施。在数学教学中引入教学主线是结构化学习观的需要，是遵从学习规律的应然选择。借助教学主线，可以更好地厘清数学知识之间的内在联系，明晰数学方法之间的相互关联，梳理数学思想之间的层次关系。因此，教师要充分发挥教学主线的作用，引领学生经历知识萌发、生长、丰盈的过程，不断完善知识网络，丰富认知体系，进而优化学习方法，提升学习效率。

2.教学主线是结构化学科观的体现

数学具有内在的统一性，但为了教学的需要，人们常常会对数学知识进行一些分割，这样的处理难免会造成知识的支离破碎。因此，教师在教学时必须超越“碎片化教学”，帮助学生建构起整体性认识，包括掌握知识的整体性结构，并能逐步学会从层次的角度进行分析和思考[1]。

在数学教学中引入教学主线是结构化学科观的需要，是统整教学内容的自然选择。数学家华罗庚就曾提出“一条龙”的教学思想，他指出，数学是一门联系紧密的学问，是一个整体，我们可以创造性地将原本割裂的数学基础课综合为一门课，构成新的教学系统。教学主线是落实“一条龙”教学思想的有效途径之一，它可以有效整合教学资源，避免知识的碎片化，还可以有机串联教学环节，避免教学的无序化，从而保证教学活动的整体性、连贯性与协调性。

3.教学主线是结构化课程观的体现

《义务教育数学课程标准（2022年版）》要求“设计体现结构化特征的课程内容”，并倡导“设立跨学科主题学习活动，加强学科间相互关联，带动课程综合化实施，强化实践性要求”[2]。显而易见，设计结构化内容，推进跨学科学习，建设综合性课程已成为当下新课改的重要任务之一。

在数学教学中引入教学主线是结构化课程观的需要，是顺应教学改革的必然选择。在跨学科教学活动中，涉及的学科领域众多，知识点繁杂，但有了教学主线，便可对原生态的教学资源加以取舍、统整、融合。借力教学主线，教学目标便有了“主心骨”，有的放矢而不会迷失方向；教学活动便有了“主干线”，主次分明而不会顾此失彼；教学评价便有了“主旋律”，着重于学生素养发展。

二、教学主线的设计流程

《义务教育数学课程标准（2022年版）》更注重大概念、大单元、大任务、大问题的设计，这就要求教师在教学设计时必须要有更宽广的教学视野，更上位的整体考量，而教学主线的引入则为解决这些问题提供了很好的实践路径。教学主线是教学资源的整合依据，是教学活动的推进线索，但它的形成不是一蹴而就的，而需要经历一个逐步聚焦凝练、不断完善的过程。具体来说，教学主线的设计流程包括以下四个设计阶段：挖掘“生长点”、收集“关联线”、整理“逻辑面”、凝成“教学块”。

下面以苏教版《数学》四年级上册“图形整理与复习”（第102页第14题—第17题）为例，具体谈谈教学主线的设计过程。

1.要在教学资源中挖掘“生长点”

数学教育专家史宁中教授告诉我们，要学会用数学的眼光观察世界，其实，这不仅是对学生数学核心素养的培塑要求，也应该是数学教师的专业追求。正如“世界上不是缺少美，而是缺少发现美的眼睛”一样，数学教学素材并不缺乏，但缺少的是发掘数学资源的眼光。

“图形整理与复习”中涉及的知识点有：直线、线段、射线、角的大小与分类、平行与垂直、观察图形……毫无疑问，这些知识点繁杂琐碎，关系错综复杂。从何处入手整合教学资源呢？解读教材后不难发现，上述知识点大都可以归类为“线”（直线、线段、射线）以及“线”的组合（角的大小与分类、平行与垂直）范畴，于是，教师把“线”作为教学主线设计的“生长点”，为接下来的统整教材做好铺垫。

2.要运用多种渠道收集“关联线”

“生长点”是教学主线设计的切入口，但生长点仅仅局限于“点”的层面，涵盖的内容往往不够丰富与饱满，为此，教师以生长点为“圆心”，运用不同手段，通过不同渠道，收集与“生长点”有关联的信息，从而为教学主线的拟定提供更多的资源支持。

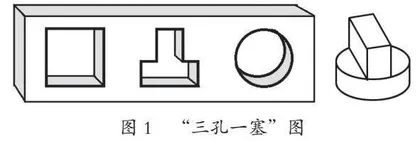
在“图形整理与复习”中，与知识点“线”有关的信息有哪些呢？通过书籍查找、网络搜索，教师梳理出了这些素材：在数学层面，线可以看成是由无数个点组成的，面可以看成是由无数条线组成的，体可以看成是由无数个面组成的；除了一维空间、二维空间、三维空间以外，还有四维空间，甚至是五维空间；关于观察物体，“三孔一塞”比较有趣，用一个塞子可以堵住三个不同形状的孔（如图1）；还有些图形比较奇妙，它们容易让人产生视觉错误……如此丰富的教学资源为教学主线的发展提供了更多的接口。

3.要根据内在联系整理“逻辑面”

数学学科本身有着自己的逻辑体系，为此，教师要基于教学资源的“生长点”以及“关联线”，寻求“逻辑面”。立足数学本质，挖掘数学知识之间的内在联系，明晰思想方法之间的转化关系，安排好主次内容、前后次序、递进脉络，进而为教学主线的进一步拟定奠定基础。

“图形整理与复习”中“生长点”与“关联线”之间又有着怎样的逻辑关系呢？受到“线可以看成是由无数个点组成的，面可以看成是由无数条线组成的，体可以看成是由无数个面组成的”的启发，教师基于极限思想，将点、线、面、体之间的递进关系设定为教学主线：点→线→面→体（三维）→多维。引领学生对平面图形与立体图形之间的关系产生全新的、整体的认识。与此同时，从近到远、从有限到无限、从微观到宏观，也巧妙地渗透了数学知识的整体性以及数学思维的层次性。

4.要根据教学主线凝成“教学块”

教学主线具有提纲挈领的作用，它能将众多的知识“点”串成“线”，连成“片”，形成“块”[3]。这里的“块”即“教学块”，也可以称之为“教学板块”，它能贯串、统领、协调各部分教学资源，实现教学内容的结构化以及教学活动的结构化。

在“图形整理与复习”一课中，依据教学主线：点→线→面→体（三维）→多维，形成了四个教学板块：从点到线、从线到面（图形）、从面到体（观察物体）、从三维到多维。在第一板块中，通过点动成线的动画演示，认识到所有的线都可以看成是由点组成的，进而比较直线、线段、射线的异同；在第二板块中，把直线、线段、射线进行搭配组合，形成不同的图形（角、平行线、垂线、长方形、正方形等），复习相关知识要点以及画图方法；在第三板块中，通过观察多个小正方体拼成的不规则物体以及“三孔一塞”图，体验到不同角度观察物体的差异性、必要性与辩证性；在第四板块中，借助“多维空间”等数学文化，体验数学带来的奇妙。

三、教学主线的实施路径

在教学过程中，教学主线可以以“教学板块”的形式加以呈现。这里的“教学板块”不同于以往的复习、新授、巩固等教学环节[4]，它展现的是知识发生发展的过程，表达的是知识之间的逻辑关系，反映的是认知新事物的一般规律，凸显的是数学教学的学科特质。“教学板块”是教学主线的具体表达，是结构化教学的实施载体。以教学板块为表现形式的教学主线，其常见实施路径有以下几种[5]。

1.以知识的生长为教学主线，教学板块内容呈现为“是什么—为什么—怎么用”

新知识的产生往往都有一个发展的过程，对于学生来说，学习数学知识也是如此，只有经历知识萌发、生长、丰盈的过程，学习才会更深刻，更生动。然而，数学的学习不是科学数学的重演，而是学科数学的再造，因此，教师需要对教学内容进行深度加工，为学生发现问题、提出问题创造机会，为分析问题、解决问题提供支架。

【案例一】苏教版《数学》六年级上册“认识比”

板块一，什么是比？

引导学生认识比、比值的意义，掌握求比值的方法。

板块二，为什么要学比？

提问：分数、除法和比一样，都能表示两个量之间的关系，为什么还要学习比呢？

教师引入三个数、四个数的连比，让学生感悟比的价值——简洁、明了。

板块三，比有什么用？

欣赏人体中的比、黄金分割比……

“是什么”“为什么”“怎么用”是人们面对未知世界时常有的困惑，也是学生学习新知时常用的探索方法。教师以知识生长的过程为教学主线，通过“什么是比”“为什么要学比”“比有什么用”三个教学板块，引领学生在知识的发展过程中渐渐逼近知识的本质，进而保证教学内容、教学活动的整体性与层次性，与此同时，也渗透了探究未知的方法、培养了探究未知的能力。

2.以体系的构建为教学主线，教学板块内容呈现为“从简起步—提升构造—融合回归”

德国著名科学家普朗克说：“科学是内在的整体，它被分解为单独的整体不是取决于事物的本身，而是取决于人类认识能力的局限性。”其实，不管是数学学科本身，还是数学与其他学科之间，都存在千丝万缕的联系，这就需要教师以整体的眼光，带领学生及时“跳出”知识的繁枝缛节，在肯定自我、否定自我、完善自我的反复过程中明晰事物的内在联系，完善知识网络，构建认知体系。

【案例二】苏教版《数学》六年级上册“长方体和正方体的认识”练习课

板块一，正方体中的点、线、面、体。

学生自主探究，完成学习单（一）（如图2），对比分析后发现：顶点的数量不变，当“线”扩大（或缩小）n倍（n大于0），“面”就会扩大（或缩小）n2倍，“体”就会扩大（或缩小）n3倍。

板块二，长方体（不包括正方体）中的线、面、体。

学生再次自主探究，完成学习单（二）（如图3），比较后发现：规律是有范围的，不是所有的长方体之间都具备上述规律，但当长、宽、高变化一样时就存在上述规律。

板块三，长方体（包括正方体）中的线、面、体。

追问：长方体中存在的规律与正方体中存在的规律有联系吗？

总结与拓展：形状一样，大小不一的平面图形或立体图形之间都存在上述规律。

学习“长方体和正方体”之后，很多学生都能认识到正方体与长方体之间具有的包含关系，但对正方体与正方体之间、长方体与长方体之间的横向联系却不甚了解。为此，教师以知识体系的构建为教学主线，设定了上述三个教学板块。首先，从正方体开始，探究“点、线、面、体”的变化，初步建立知识体系；接着，比较几个长方体（不包括正方体），从而打破原有的规律，使学生怀疑刚刚建立的知识体系；最后，借助正方体与长方体间的联系，在特殊中总结出一般规律，感悟相似形、相似体的特征，在“破”与“立”之间实现认知体系的重新建构。