小学数学“量与计量”的结构化教与学
作者: 王海巧
摘 要 “量与计量”是人教版数学教材的重要组成部分。在厘清小学阶段“量与计量”各知识点之间关系,对“量与计量”教学内容进行分类比较后,结合这部分内容在教学方法上的相似性,实现教法和学法的结构化,进而努力建构起“量与计量”的结构体系,组织相应的学习系统,从而促进知识、思维、方法上的整体建构。
关 键 词 小学数学 量与计量 知识结构化 内容结构化 教法结构化 学法结构化
引用格式 王海巧.小学数学“量与计量”的结构化教与学[J].教学与管理,2022(29):40-43.
结构化教学是根据知识的形成规律和学生的认知发展规律,通过沟通各元素间的联系来设计教学的一种方法[1]。“量与计量”是人教版数学教材的重要组成部分,其教学内容繁多,分布于各册数学教材,又因其大多呈“小单元”编排,教学时极易出现浮于表面、重复零散化、忽略教材联系等低效现象。数学是一门有结构的学科,教师如何关联统整“量与计量”各版块的知识、思维和方法,合理划分教学内容?教学方法是相似的,如何从不同的视角出发,采用灵活的处理方式,合理架构各个知识领域的活动序列?如何突破“量与计量”的教学难点?本文试着从这些方面入手,提高全景维度上的整合能力,努力建构起“量与计量”的结构体系,组织相应的学习系统,从而促进学生学习力、实践力的整体提升。
一、综观全局,整体梳理
1.从“点状”到“网状”的知识结构化
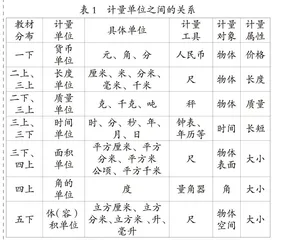
在人教版数学教材中,“量与计量”的内容呈“散点式”分布于各册教材。教材从一年级下册开始编排相关内容,由浅入深又相互关联,1—3年级的教学内容主要与数量运算相关,4—6年级的教学内容主要与图形测量有关。“量与计量”的学习内容抽象且零散,如果教师在教学中只注意一个课时,只关注一个点,忽略教材内容的上下联通,就会导致学生碎片化地理解知识。教师应站在更高更全面的角度去剖析教材中的各个知识点,找到其中的相同和不同之处,找寻其中的关联(见表1)。
(1)同一体系的连续性。纵向上看,二年级上册的厘米、米和三年级上册的分米、毫米、千米同属长度单位这一体系,往长远看,长度、面积、体积单位的知识从一维到二维、三维螺旋上升、层层递进,属于同一体系,具有连续性。长度是测量一维空间,主要测量线段,出现曲线时,需要化曲为直。“线—面—体”的形成过程,则对应一维、二维、三维的空间观念。同时,三者的度量又以一维的长度测量为基础,先学会测量长,再测量二维的长、宽,再到测量三维的长、宽、高。
(2)不同体系的统一性。单位的出现源于人类发展的需要,计量标准经历了多样性,比如“一拃”“一庹”“一步”等,最后计量单位产生了统一的必要性。不同的体系有不同的计量工具,如尺、秤、量角器、钟表等,尽管属性各异,但计量工具上都有度量起点“0”、刻度、数量这三个要素。
(3)不同领域的相融性。度量包括计量和计数,计量注重量感的形成,是具体化的度量;计数注重数感的形成,是抽象的度量。把量抽象化、符号化后可用数来表示;数是由量抽象而来的,把数具体化,可用量来表达[2]。计量和计数属于不同的领域,但是他们的单位也是相通的。
2.从“局部”到“整体”的内容结构化
“量与计量”包含的七种量按照内容分类划分,可分为三大类:经验关联型(货币、时间、质量)、度量操作型(长度、面积、体(容)积)、抽象勾连型(角),七种量的进率既有区别又有联系。
(1)经验关联型。“量与计量”中的货币、时间、质量的学习都要联系日常生活,其中货币、时间重在生活中提前孕伏,在课前布置预习单(如年月日的认识),让学生积极去认识单位以及相互间的换算,并最终应用于解决实际情境中的问题。而质量的学习重在建立生活经验,除了认识质量单位和换算,还要学会用测量工具比较和测量物体质量,并学会估计。
(2)度量操作型。“量与计量”中的长度、面积、体积同属度量操作范畴,需要学生经历多次测量活动,使他们体验从具体到抽象的数学思维过程。长度的学习要让学生体会尺子的产生过程。面积单位的学习中主要是平方米和平方厘米,其中平方千米和公顷是难点,需要引入“平方十米”,突破学生思维的断层,顺利和长度单位链接。比如由面积单位中的1平方米很容易想到对应的长度单位1米,1平方分米想到1分米,1平方厘米想到1厘米,1平方千米想到1千米。而1公顷的出现,学生不知道与它对应的长度单位是什么。其实,在教学中引导学生理解面积1公顷的正方形的边长是100米,需要引入“1十米”,学生就比较容易理解1公顷。1公顷介于“1平方十米”和1平方千米之间,相对应的长度单位也介于“1十米”和1千米之间。体积是抽象的,指物体所占空间的大小,可以从外面去测量;容积是学生日常生活中接触到的量,指容器能容纳物体的大小,从容器的里面去测量。体积单位和容积单位相互区别又相互联系,计量杯子的容积时一般就用所盛液体的体积单位,杯子内水的体积就是杯子的容积。
(3)抽象勾连型。“量与计量”中的角无体系,需和长度、面积发生勾连。比如“认识厘米”和“角的度量”可以联系起来,教学“认识厘米”时有三问:测量线段的工具是什么?怎样测量线段?为什么不同的测量方法都可以量出线段?这三问同样适合于“角的度量”的教学,二者的测量工具构造原理一样,尺子的产生过程是量角器诞生的基础。
七种量的进率都不同,其中长度单位、面积单位、体积单位同属一体系,进率分别是10、100和1 000。角的单位是度,和其他没有关联。时间单位的进率比较特殊,有60、24、28、29、30、31、12,还有一年=365/366天。进率都是10的是长度和货币单位,因此长度单位的学习需与货币单位相关联;体(容)积和质量单位的进率是1 000,容积与质量相关,比如1升水重1千克。人民币的学习中学生在理解等价关系1元=10角,10元=100角的基础上,渐渐理解十进制关系,在学习元、角、分的进率时可以和一年级下册学习的数位顺序表百位、十位、个位相对应,这样学生更好理解。
对“量与计量”教学内容进行划分比较,可以厘清其间错综复杂的关系,整体把握教材,使教学过程既见树木,又见森林。
二、整体考虑,长远设计
结构化学习是整体化的思考,是对六年小学数学知识的通盘考虑,虽然知识模块不同,但是计量的本质思想是一致的。在设计教学时,可思考以下问题:你能想到和此内容有关的已学和未学内容吗?这些联系对此内容有什么作用?怎样去设计有结构的教学?思考清楚这些问题后,再以统筹的视角整体考虑
1.从“一课”到“整体”的教法结构化
(1)基于课时视角,把握本质元素。学生的知识储备靠日常教学中一课时一课时的积累获得。基于课时的视角,数学学习不应是碎片化,处于撕裂状态的,而应放在整个单元整体中去理解每个知识点,把握每课时的本质要素,打开认知通道[3]。
(2)基于单元视角,挖掘关联元素。如果把课时内容看成一个点,那么单元内容就是一条线。教师需要引导学生从课时走向单元,单元间有些课时是相通的,深入挖掘种子课的教学,加以发散,渐至“少教”甚至“不教”,可以以主题种子课覆盖同领域的其他内容。例如长度单位的认识中,起始课是二年级上册的认识厘米,认识厘米和米在同一单元,分米和毫米在三年级上册的同一单元,有了种子课的模式,可用种子课的方法迁移到米、分米、毫米的认识中。
(3)基于整体视角,注重体系建构。结构化学习是整体化的思考,将知识点成链成网,纵向从点、线、面、体去深入挖掘,横向从知识、思维、能力去深度思考,发现计量单位的教学基本上是相似的。如教学步骤的安排:体会统一计量单位的必要性;认识计量单位;建立计量单位的表象;单位选择的思考;用单位进行度量;进行单位换算。
涉及到具体领域,活动板块之间可以调整,合理架构活动序列。例如在长度单位的学习中,可以按“感受多样的度量方法—思考统一度量单位的必要性—建构标准量的表象—认识度量工具—认识度量单位—在实际中使用”的模式展开学习,面积、体积的学习也适用。
2.从“浅表”到“深化”的学法结构化
构建结构化学习的框架是结构化学习的关键性一步。它们有学习方法的共性,虽然内容不同,但在整体结构上是相通的,综观计量单位的教学,都可以通过以下步骤展开教学:体会统一计量单位的必要性;认识计量单位;建立计量单位的表象;单位选择的思考;用单位进行度量;进行单位换算[4]。
(1)认识计量单位,由“多样”走向“统一”。认识计量单位,需要学生感受度量方法的多样性,在感受、比较后,体会统一计量单位的必要性。比如“认识面积”第一课时让学生经历小正方形、小长方形、小圆形度量面积的过程,初步体会用正方形作面积单位的优点(如图3)。引发认知冲突一般是第二课时的内容,6个正方形比20个正方形的面积大(如图4),让学生充分体会统一面积单位的必要性。以结构化学习的视角来看,可以把两课时的内容放整合在一节课上去学习。
(2)建立单位表象,由“一个”走向“多个”。建立计量单位的表象,首先要建立“一个单位”的概念,这是学生学习关于“量”的知识的基础。通过动手操作建立表象还不够,还需要和直观观察、想象记忆、举实例、现场活动等结合。制作面积单位1平方厘米、1平方分米、1平方米的实例是最基础的,学生在多维的活动表征中,初步建立较准确的表象。通过做、摸、想、比、说、估等多重表征方式,让学生有实物可依,初步感知、存储“参照物”,为接下来的学习打下基础。
其次,丰富对“几个单位”的体验。比如在认识了“1平方厘米有多大”后,可以请学生画10平方厘米、估计自己的橡皮有多大(4平方厘米),在学生逐渐对1平方厘米、4平方厘米、10平方厘米有所感悟后,再猜数学书的表面有多大、课桌的表面有多大、黑板的表面有多大。通过画、猜、量等来定量刻画,让学生更加充分地去感知。有了实物的体验,也为接下来脱离实物在头脑中进行抽象操作打下基础。建立单位表象,由“一个单位”走向“多个单位”,也由静态走向动态。
(3)运用度量单位,由“抽象”走向“直观”。 运用度量单位包括对单位的选择和用单位进行度量。学生通过建立表象,不断地丰富参照物和直观模型。在运用度量单位时,拉长、细化相关的直观体验,从“抽象”走向了“直观”。
(4)进行单位换算,由“寻常”走向“灵动”。认识计量单位和计量单位间的关系,换算才有依据。比如长度和加法、减法相关,长度可看成是几个作为计量单位的长度标准进行加、减的结果;面积要和加法、乘法相联系;体积要和乘法相联系。计量单位除了和加法、减法有关,也和乘法、除法相关,在化、聚时,既可看成是单位量的累加,也可看成是包含除的拆出单位量。“寻常”的单位换算,因为有了加、减,有了乘、除,变得更为“灵动”。
三、突破“量与计量”教学难点
1.估计的策略
估计往往和测量相结合。估计难,难在没有参照物和对比量。学会估计,首先要建立“一个单位”,用单位量去估;其次当单位量过小时,要用身边熟悉的常用典型物品去估,可将测量和估计活动前置或后移,让学生有时间做准备,并在班级群中分享测量和估计的过程。虽然估计结果存在个体的差异性,但是结果却有相似性,这样可以进一步加深抽象数字和具体数量间的联系。估计对发展学生的数学理解、培养思维灵活性有重要作用。比如在“克和千克”的教学中,4人为一小组,教师事先把桌子上的5袋物品按从重到轻排一排,学生在粗略感知轻重后,着重对4号(1千克)、2号(14克)进行教学,在之后的练习中让小朋友运用刚才建立的单位量来估估其他3个袋子各重多少,并把结果记录在学习单上。通过对1千克的感知,学生能大致推断出2千克和500克,而物品1和单位量1克相去甚远,和物品2的重量14克相比也难以判断,就需要靠身边熟悉常用的物品——一包瓜子100克、一包饼干110克这些典型物品来估。