新课标背景下小学生计算思维学习进阶的构建研究

摘要：《义务教育信息科技课程标准（2022年版）》将计算思维作为信息科技学科的核心素养之一，并按照不同学段制定了不同的学习目标与具体学业成就表现，提出要关注学生的认知发展过程。学习进阶作为国际教育领域的重要课题，可以刻画出学生的思维发展过程，呈现出不同阶段学生应达到的水平，为教育者提供明确的教学目标和进阶路径。因此，构建小学生计算思维学习进阶可以刻画小学生计算思维发展过程，更好地促进计算思维的培养。本研究主要运用文献分析法等研究方法，通过对国内外文献和国内外课标的梳理，根据学习进阶的构成要素，从进阶维度、成就水平和进阶终点三个方面构建了计算思维学习进阶，以期促进计算思维的培养。

关键词：新课标；小学生；计算思维；学习进阶

中图分类号：G434  文献标识码：A  论文编号：1674-2117（2025）05-0000-04

在人工智能时代背景下，随着新兴技术的迅猛发展，人们的生活发生了显著的变化。为了适应社会变革，提高国家竞争力，必须加强对学生计算思维的培养。

《义务教育信息科技课程标准（2022年版）》（以下简称“新课标”）提出要培养学生核心素养，将计算思维作为信息科技学科的核心素养之一，并按照不同学段制定了不同的学习目标与具体学业成就表现，提出课程内容要关注学生的认知发展规律。而学习进阶旨在描述学生的思维发展过程，因此，构建小学生计算思维学习进阶可以使教育者和研究者更深入地理解学生的学习过程，培养学生计算思维，从而制订更有效的教学策略，提供明确的教学目标和进阶路径。

研究背景

1.计算思维是人工智能时代学生必备的核心素养

在人工智能时代，人们的生活、学习和工作方式正在以前所未有的速度改变，在此背景下，计算思维已成为学生必备的核心素养，它对于提高学生的逻辑思维能力、问题解决能力、创新能力和跨学科学习能力具有重要意义。教育部颁布的《义务教育信息科技课程标准（2022年版）》提出要培养学生信息科技核心素养，其中计算思维是重要的核心素养之一，课标还按照不同学段制定了不同的学习目标，提出课程内容要关注学生的认知发展规律。

2.学习进阶是刻画学生思维发展过程的重要途径

学生的认知发展过程是一个复杂的过程，如何细化学生的认知过程呢？“学习进阶”（learning progressions，简称LPs）可以描述学生在较长的时间跨度内认知是如何发展的，进而刻画出学生的思维发展过程。学习进阶为教育者提供了明确的教学目标和进阶路径，有助于他们合理设计教学活动和安排教学进度。

3.学习进阶助力计算思维的培养

学生的计算思维学习进阶可以描述出其不同阶段的计算思维发展过程，有助于教育者和研究者更深入地理解学生计算思维的变化过程，从而制订更有效的教学策略，促使学生持续发展。

概念界定与理论基础

1.计算思维

2006年，周以真教授最早提出了计算思维，她认为计算思维是解决问题的过程。此后，计算思维受到了国内外的广泛关注，各国学者都对计算思维展开了研究。

计算思维的概念从不同角度理解是不一样的，但本质都是在解决问题的过程中将问题分解、抽象建模，并设计算法寻求最佳解决方案的思维方法与活动，是利用计算机科学来进行算法、自动化、评估、建模与仿真、抽象、概括的能力。本研究认为，计算思维是运用计算机科学的方法解决问题的过程，这一过程涉及问题分解、抽象建模、设计算法并寻求最佳解决方案的思维方法。

2.学习进阶

学习进阶的概念最早起源于美国，美国国家研究理事会（National Research Council，简称为NRC）针对教育中知识宽泛却不深刻的问题颁布了新的国家科学教育标准，进行了教育改革，并提出了学习进阶概念，将学习进阶定义为在一段时间内，学生在学习或研究某一主题时呈现出的思维发展路径。同时，根据学生年级的增长加深了课程内容，使得知识结构连贯，符合学生认知发展特点。

从概念角度理解，学习进阶是学生在学习同一主题的概念时所遵循的连贯的、典型的学习路径。从思维发展角度来看，学习进阶是描述学生对某个主题连续的、更加熟练的思考方式。根据对文献与课标的梳理，学习进阶的定义主要分为方法说、过程说、假设说等。本研究将学习进阶定义为在较长的时间跨度内学生的思维发展过程。

3.理论基础

皮亚杰提出，个体自出生后在适应环境的活动中，对事物的认知及面对问题情境时的思维方式与能力表现，会随年龄增长而改变。其认为儿童的认知是在已有图式的基础上，通过同化、顺应和平衡等机制，不断从低级向高级发展的一个建构过程。

皮亚杰认为儿童的认知发展可以分为四个阶段，分别是感知阶段、前运算阶段、具体运算阶段和形式运算阶段。感知阶段（0～2岁）：儿童通过感知和动作与外界发生作用，主要认知结构是感知运动图式；前运算阶段（2～7岁）：儿童的思维具有符号性，能用表象和言语表征世界，但思维仍具有直觉性、自我中心性和不可逆性；具体运算阶段（7～12岁）：儿童的思维开始具有较大的变易性，出现了可逆性，能解决守恒问题，能凭借具体事物或形象进行分类和理解逻辑关系；形式运算阶段（12～16岁）：儿童的思维已能摆脱具体事物的束缚，进行抽象的逻辑思维，能运用符号进行命题演算和逻辑推理。

小学生计算思维学习进阶的构建

学习进阶的构成要素包括进阶维度、进阶终点、成就水平、表现期望和测评工具。笔者基于结构中心设计原则，根据学习进阶的构成要素构建小学生计算思维学习进阶。通过系统地回顾国内外课程标准及相关文献，构建小学生计算思维学习进阶，描绘小学生计算思维的发展轨迹，使课程与教学更关注学生计算思维发展轨迹。

1.国内外课标分析

在美国、英国、澳大利亚等国家，计算思维已被纳入义务教育课程标准，并根据不同年级学生的特点设定了相应的计算思维目标。国外课标普遍倾向于认为计算思维是解决问题时的思维活动。新课标也根据不同阶段学生计算思维水平设置了学段目标，并将计算思维定义为问题解决过程中的思维活动，其中包括抽象、分解、建模等。

多数国家的课标倾向于将小学阶段划分为三个学段，主要从问题分解、算法设计、抽象思维等方面对计算思维目标进行划分，要求学生掌握用算法思维解决实际问题的能力，拥有算法结构的理解能力。基于上述背景，本研究旨在探讨计算思维在解决实际问题过程中所需掌握的各项技能，包括问题分解、算法设计、抽象思维等，重点分析计算思维所包含的多种技能。

2.进阶维度的提取

进阶维度是核心概念包含的子概念，即学生计算思维涵盖的横向维度，通常通过学生横向进阶维度上的发展来了解其学习进阶路径。本部分的主要任务是提取计算思维进阶维度，明确计算思维的组成部分。

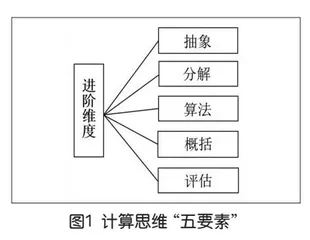
通过梳理与分析国内外课标及相关文献，笔者发现计算思维通常被理解为在问题解决过程中所需的一系列技能，其中，抽象、算法、模式识别和分解四个维度的出现频率较高。基于此，本研究聚焦于从问题解决过程中的技能层面进行深入的维度提取。Selby&Woollard的“五要素”与新课标中对于计算思维的定义有较高的契合度，并提供了一个清晰的技能分解框架。因此，本研究采纳Selby&Woollard的“五要素”作为构建自身进阶维度的基础，如图1所示。

3.成就水平的划分

成就水平是指随着学生学段的增加，其思维方式的发展变化，是学生在各个进阶维度下的思维发展过程。本研究主要参考各国课标对计算思维教育目标的规定，基于皮亚杰的认知发展理论与SOLO分类理论，确定了计算思维发展变化的阶段，具体如图2所示。最终对确定的进阶维度，提取不同阶段的内容标准，并构建出成就水平模型以及每个层次上对应的学生具体行为特征。

小学生计算思维学习进阶的验证

本研究通过构建进阶维度与成就水平，最终构建了小学生计算思维学习进阶，描绘了小学生在计算思维发展过程中的成长路径。在此基础上，通过德尔菲法和访谈法对小学生计算思维学习路径的科学性和适用性进行了评估与调整，重点探讨了学习进程中的发展阶段划分、最终目标设定及各阶段预期达成的能力水平是否恰当，同时，修正了学生在各个水平上应表现出的具体能力描述。通过对访谈记录进行多层次编码分析，进一步优化和完善了小学生的计算思维学习进阶体系。最终，确立了小学生计算思维发展路径，具体内容如上页表所示。

参考文献：

[1]陈国良，董荣胜.计算思维的表述体系[J].中国大学教学，2013（12）：22-26.

[2]李国杰.21世纪上半叶信息科学技术展望[J].中国科学院院刊，2010，25（01）：78-86.

[3]王飞跃.面向计算社会的计算素质培养：计算思维与计算文化[J].工业和信息化教育，2013（06）：4-8.

[4]中华人民共和国教育部.义务教育信息科技课程标准（2022年版）[S].北京：北京师范大学出版社，2022.

[5]张茜.小学生计算思维学习进阶的构建研究[D].无锡：江南大学，2023.

[6]张茜，刘向永.小学生计算思维学习进阶的构建研究[J].汉字文化，2023（10）：181-183.