算法思维可视化：促进儿童的编程概念转变

摘要：本文以“初识变量”一课的教学为例，依托形象化的算法选择、直观化的算法描述、支架化的算法实现进行教学设计，旨在将算法思维的进阶可视化，帮助学生理解算法思想，促进编程概念转变。

关键词：小学信息科技；算法教学；概念转变

中图分类号：G434  文献标识码：A  论文编号：1674-2117（2024）08-0035-04

案例背景

在小学信息科技的算法教学中，学生会在短短几个月内接触到许多全新的编程概念，如判断、循环、变量等。这些词语原本的概念学生已经理解，但它们的编程概念却是全新的，这时，就需要教师引导学生进行概念转变，促进学生对错误或不完善的前概念进行改造与重构，以正确认识编程概念。

然而，在实际教学中，学生的编程概念转变却很难推进。在前概念的影响下，学生很容易产生“简单问题直接写程序、复杂问题大脑一片空白”的情况。笔者认为，问题的根源出在学生的算法思维层面。因此，笔者尝试在教学中以可视化的方式引领学生进行算法思维进阶，创设真实的生活情境，将针对编程概念与算法的思考详细化、具体化，将思维的每一次进阶形象地展示出来，帮助学生理解算法思想，重构编程概念。

案例描述

在五年级信息技术《初识变量》一课中有“变量”这一编程概念，这是其第一次在课本中出现，本课的教学目标为“理解图形化编程中变量的概念，并能够综合运用变量进行程序设计”。“变量”这一概念对五年级的小学生来说，较难理解，在非编程情境下，人们通常不会用这样的专有名词去称呼它，但其实它在我们的生活中几乎无处不在。例如，在购买同一件商品时，购买数量不同，总价也不同。其中，“购买数量”和“总价”就是变量。一般来说，学生在没有运用信息化手段去解决问题时，很难触及这个概念。因此，笔者在教学伊始设置了一个真实的购物情境，引领学生发现问题，体验“变量”的使用。

1.变量我会建：购物情境交互，概念的初体验

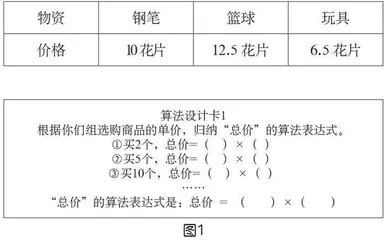
师：今天，老师开了一家“小飞象”商店，同学们可以用之前课上得到的花片来购买商店中的物资（如下页表）。（规则：每位同学都只能在商店中选购一种商品，但同一种商品可以购买多个，多买可能还有一些优惠）请你来买一买。你想买什么？

生1：我有125个花片，我想买篮球。

师：谁来帮他算一算，他最多可以买几个篮球？（学生回答）同学们反应都很快！还有谁想买篮球？

生2：我有100个花片，我想全部买篮球。

师：他可以买多少个呢？

生3：8个。

师：我们班有的同学有365个花片，他最多可以买多少篮球呢？（学生不能即刻算出购买结果，在这个过程中，他们会产生用信息化手段去解决问题的意识）在不同情况下，你在商店购买的篮球“个数”都不同，像“个数”这样没有固定的值，可以改变数值的量叫做变量。请同学们打开编程软件，完成以下活动。

活动要求：参考课本第45页，新建变量“个数”，并将“个数”的值设定为你想购买的数量。

2.总价我会算：从算式到算法，引领概念过渡

在体验了新建变量后，学生对“变量是什么”有了初步的认知，但多数学生并未深入理解。因此，笔者为学生提供“算法设计卡”，将编程教学课堂的活动分为“算法设计”和“程序实现”两个步骤，旨在引导学生的算法思维过程。

（1）算法设计

师：小买家们已经新建了“个数”这个变量，并能任意输入“个数”的值。那么，买下这些商品的总价是多少，你会算吗？以体育小组买篮球为例，我们一起算一算。如果个数是不固定的值呢？请同学们拿出算法设计卡1（如图1），填一填。（学生汇报分享）

在学生的算法设计卡上，笔者看到了“总价=单价×数量”这样的填写（如图2），经过询问得知，学生在数学课上学习过购物主题的应用题，他们背诵的数学公式是“总价=单价×数量”。这说明，学生在此前的学习过程中并没有完全摆脱前概念的影响，他们对“变量”编程概念的认知仍不清晰，无法判别哪个量是定值，哪个量是可以改变数值的量。因此，笔者化“错误”为“课堂生成”，采用生生互助的方式，探讨学生的错误出现在哪里，纠正学生顽固的前概念。

师：xx同学的算法表达式并没有完全错误，你们能不能发现，现在只有哪个是变量？

生：只有“个数”是变量，同一小组买的东西相同，单价是固定的。

师：怎么修改呢？

生1：要把“单价”改成他们小组的10。

生2：“数量”也要改成已经新建的变量，叫做“个数”。

生3分享：（文具小组）总价=10×个数；（体育小组）总价=12.5×个数；（游乐小组）总价=6.5×个数。

为了让学生的算法思维更为清晰与直观，笔者引导学生将总价的算法表达式在设计卡上写下来。这样，在接下来的程序实现环节，学生可以根据算法设计卡上的算法表达式，与程序块一一对应，完成算法的程序化表达。

（2）程序实现

活动要求：依照自己小组的算法表达式，在程序中设定变量“总价”的值。

活动反馈：

生1：“总价=”对应的程序块是“将总价设定为”。

生2：“×”对应的程序块是“数字与逻辑运算”类别下的乘法运算。

生3：12.5直接输入数字，“个数”对应我们之前新建的变量。

学生对照算法表达式，采用顺次对应的方式，思考算法对应的程序表达。将算法表达式分解为一个又一个小问题，然后再进行融合，完成了算法的程序实现。

3.优惠我会选：抽象数据的可视化组织，强化概念转变

经历了之前的环节，在算法思维层面，从自然语言描述算法，到数学表达式表示算法，再到程序语言实现算法，学生已经能够用编程实现简单的算法，但对编程概念“变量”的概念转变还没有最终完成。笔者认为这是由于总价的算法表达式与数学过于相似，编程特性较弱，学生的概念转变还需要与之前的编程经验进行更为紧密的联系。因此，笔者结合顺序、选择、循环三大程序结构，设计了复杂算法下的变量应用。在解决这个问题的过程中，笔者将教学活动进行了分解，即将其分解为算法设计、程序实现和策略选择。

师：如图3所示，小飞象市场提供了两种不同的优惠方案，你们要怎么买才能更优惠呢？

（1）算法设计

活动要求：拿出算法设计卡2（如图4），两人小组分工，根据两种不同的优惠方案，设计对应的算法表达式。

活动反馈：略。

（2）程序实现

活动要求：根据两种优惠方案的算法设计，修改程序。

活动反馈：

①买8送1的程序实现：学生上讲台拼板贴（如图5），分享思考过程。

②全场9折的程序实现：学生上讲台拼板贴（如图6），分享思考过程。

（3）策略选择

活动要求：小买家一共有100个花片，最多能买多少个呢？选择哪种优惠能买更多个呢？请你分别运行两种优惠的程序，关注“个数”和“实付金额”的值，填写算法设计卡3。

师（总结）：我们分析发现，不同的商品，由于单价不同、购买数量不同，优惠策略的选择也不同。在生活中，同学们也可以运用“变量”去编程，帮助自己进行策略的选择。

本环节分为算法设计、程序实现和策略选择三个步骤，将文字语言转变为数学语言再转变为程序语言，最后借助程序工具进行策略的对比与分析，锻炼了学生的文本思维、算法思维和计算思维。优惠方案是文字语言，把它提炼为算法会牵涉数学学科的知识。在备课中，笔者和数学老师一起探讨，设计了学生能够理解、表达的两种优惠方案，让学生通过小组分工合作，能够用自然语言描述算法。算法的程序表达用到了多个程序块的嵌套，这方面学生的掌握情况差异较大，所以在课堂中运用同伴互助的方式，引导学生完成算法的程序化表达。

案例反思

1.算法选择形象化：交互情境贯穿概念转变

思维具有情境性，学生编程概念的转变需要借助特定真实的问题情境，合理情境的创设有助于教学中概念转变的推进。算法的基本思想原理性强，较为抽象，通过生动形象的情境可以将文字描述的算法原理动态立体地展现出来，帮助学生体会编程概念。在算法选择阶段，通过层层递进的问题及追问，抽丝剥茧地引导学生进入算法思维状态。就本课而言，“变量”这个词是学生从未接触过的概念，如果直接出示学科概念学生往往难以理解，而购物情境是学生在日常生活中常常遇到的，《初识变量》一课选择这个情境，正是生活的真实写照。同时，笔者将复杂的购物问题分解成几个小问题——先用变量表达个数，再用数学算式计算总价，最后用逻辑算法甄别优惠策略，这种分解使得复杂问题变得简单。接着笔者引导学生针对每个子问题进行算法选择，最终形成了解决原始问题的方案。购物这一交互情境贯穿对问题的抽象过程，也贯穿学生的概念转变过程。

2.算法描述直观化：多维表达促进概念转变

算法的描述是对算法核心思想的提炼，也是算法思维的重要环节。在算法教学中，提倡学生使用自然语言、列式、列表、过程图等多元化算法描述的方式，清晰概括每个环节对应的信息要素。这样的多维表达有助于学生选择适合自己的方式，更好地梳理算法流程走向，消解错误的前概念的副作用，促进概念转变。因此，在新建“个数”变量时，笔者摒弃了直接下达任务要求的教学方式，而是引导学生通过计算呈现具体的三个算式，让学生从具体可感且不断变化的“个数”出发，抽象出“变量”的概念。

3.算法实现支架化：能力迁移验证概念转变

算法的实现通常是程序设计的最后一环。算法实现的程序调试验证活动主要是在比较与发现中不断解决问题的过程，通过一系列连贯性的问题链启发学生算法思维的进阶。在算法实现环节，可通过设计适切的、多元化的引导思维发展和知识获得的学习支架，运用恰当的教学方法和思维技巧，将学生的算法思维可视化，帮助学生在编程概念转变中降低外在认知负荷，提高相关认知负荷。因此，在应用“变量”的程序编写中，笔者将算法的实现支架化，引导学生理解算法描述的程序化表达，借助师生互助、生生互助的方式，学生可以把多元化的算法描述用程序语言表示出来。在此基础上，还给学生提供了两种优惠策略，让学生使用不同的算法、不同的程序支架测试结果，并将结果记录在另一支架中。程序支架给学生的算法思维指明了方向，而支架化的算法实现使得不同算法之间的对比更为明晰。三个小组的汇报直观清晰地体现了组员的算法思维过程，思维迁移直指最优算法的选择策略。这一能力迁移的过程，不仅是对概念转变的验证，也是对前一阶段中未完成概念转变的学生进行概念转变的强化。

结束语

本案例选择了合适的真实情境来教授抽象的编程概念，引导学生逐步完成将文字语言转换为数学语言再转换为程序语言的过程。从思维层面上来说，这是聚焦于算法思维三阶段，即算法选择、算法描述、算法实现的过程。它强调将算法选择形象化、算法描述直观化、算法实现支架化，将学生算法思维的进阶可视化，促进学生的编程概念转变。

参考文献：

[1]中华人民共和国教育部.义务教育信息科技课程标准（2022年版）[S].北京：北京师范大学出版社，2022.

[2]王树梅，王书芹.算法可视化在数据结构课程教学中的应用[J].计算机教育，2022（07）：190-193+198.

[3]梁旭.小学生算法思维养成路径与策略解析[J].中小学信息技术教育，2022（08）：78-79.