基于课程标准的初中生计算思维现状研究

摘要：随着《义务教育信息科技课程标准（2022年版）》的颁布与教学实践的推进，中小学生的计算思维的发展越来越受重视。本研究团队基于信息科技课程标准开发了初中生计算思维评价工具，并选取部分地区的初中生进行计算思维发展现状调查，结果表明，不同年级的学生的计算思维水平存在显著差异，且计算思维“模型化”水平发展较高、自动化和系统化水平偏低。因而说明，目前中小学的信息科技课程对计算思维发展具有正向作用，但是不同模块的教学存在偏差，需要调整。

关键词：课程标准；计算思维；中学生；发展现状

中图分类号：G434  文献标识码：A  论文编号：1674-2117（2024）14-0027-05

引言

西蒙·派珀特教授（Seymour Papert）于1996年首次提出计算思维概念，但被广泛接受的是周以真教授（Jeannette M.Wing）2006年在Communications of the ACM杂志上对计算思维（Computational Thinking）的界定：计算思维是运用计算机科学的基础概念进行问题求解、系统设计，以及人类行为理解等涵盖计算机科学之广度的一系列思维活动。[1]在我国，随着基础教育改革和教育数字化转型的推进，计算思维发展已经成为中小学教育的重要内容，成为个体在复杂的技术文化中获得成功应具备的基本技能。[2]在《义务教育信息科技课程标准（2022年版）》（以下简称“新课标”）中，信息科技课程的四大核心素养被明确界定为信息意识、计算思维、数字化学习与创新以及信息社会责任。特别值得一提的是，新课标将计算思维这一关键能力从高中阶段下放至中小学阶段，此举旨在为学生打下坚实的计算思维基础。同时，新课标也清晰地界定了高中与义务教育学段在计算思维发展上的不同要求，确保教育内容的连贯性和针对性。

初中阶段对计算思维的着力培养是学生计算思维水平发展的必要积累，旨在为学生后续进入高中阶段深入学习程序设计和算法打下坚实的基础。及时了解初中生计算思维发展现状，发现存在的问题，可以针对性地解决教学实践中的问题，促进学生计算思维发展，同时有利于信息科技课程教学改革发展与教育数字化转型。因此，本研究在团队合作的基础上展开了针对部分地区的初中生计算思维发展现状调查，并通过数据分析发现问题，给出了信息科技课程教学改革建议。

研究方法和工具

1.要素界定

计算思维属于思维范畴，其抽象性使得其定义并不具备直接的操作性。不论是其最初的概念，还是周以真提出的定义，都未能提供教学中可直接运用的具体指导。然而，在计算思维的构成上，学者们提出了诸多见解。任友群教授指出，计算思维是一种独特的解题思路，有助于深入剖析复杂问题，进而构建出具有形式化、模块化、自动化和系统化特征的解决方案。[3]在《普通高中信息技术课程标准（2017年版）》中，同样看到了计算思维在问题解决中表现为形式化、模型化、自动化和系统化。[4]而新课标则进一步细化了这一过程，强调了在问题解决中的抽象、分解、建模和算法设计等思维活动。[5]陈兴冶的学习设计模型提供了一个更为具体的框架，将问题解决过程划分为模块化、形式化、模型化、自动化和系统化等阶段[6]……这些观点和课程标准在很大程度上是重合一致的。

由于初中阶段在计算思维培养中起着桥梁作用，需要注重与高中课程标准的对接，因此，为了确保信息科技课程与信息技术课程在计算思维培养上的连贯性和系统性，笔者采用了陈兴冶对计算思维过程的分析，将计算思维的要素分解为模块化、形式化、模型化、自动化和系统化。

2.研究方法

本研究采用问卷调查作为主要的研究方法。问卷调查法，又称问卷法，是一种系统性的调查手段，它主要是通过研究者精心设计的问卷，向特定的调查对象收集信息或征询意见。此方法的核心在于以书面的形式提出问题，从而有效地收集和分析所需的研究资料。

3.研究工具

本研究采用了研究团队所开发的基于课程标准的初中生计算思维测评工具。该测评工具依据课程标准及本研究对计算思维要素的划分，确定了模块化、形式化、模型化、自动化和系统化5个一级指标，然后依据课程标准对计算思维的学业质量描述，进一步分析提炼出11个二级指标，并在此基础上，依据课程标准的内容描述以及初中生自身的认知水平与解决问题能力，对每个二级指标的内容进行说明，进一步确定了22个测评标准，最终经专家审议形成完善的计算思维测评指标体系，具备一定的可测性和科学性。

测评工具以测评指标为依据，以初中生的相关学科经验、课程经验和问题解决能力经验为支撑，设计了面向七、八年级的两套测试，每套测试题有15道题目，对应的每个一级指标下各有3道题目，其中题目按照能够达到初中生能力25%、50%、75%的难度层级设计为易中难各一道，并且由高到低赋予了4个分数，统计分析后以此来反映学生的计算思维水平。

4.试测

研究团队选取某中学七年级一班和八年级一班（共75名学生）进行评价工具的试测。试测的评价工具共15道题目，设置35分钟内提交，最终回收64份问卷。试测结果显示，大部分学生在规定时间内完成并提交测试题，说明题量的设置较为科学。

（1）信度分析

对测评工具信度进行分析，来验证测验结果的可靠性和稳定性。使用克隆巴赫α值来验证可靠性，它的具体数值范围和对应的测评结果为：在0.9以上则信度极好，介于0.8至0.9之间则信度较好，不用删减任何题目，介于0.7至0.8之间则可以接受，0.7以下，则该测评工具不能被接受。在本研究中计算思维评价工具的项数为15，克隆巴赫α值为0.815，说明该测试卷的信度较好。

（2）效度分析

结构效度反映的是实验能否真正测量出所构建的理论，在本研究中用以说明各题项设置是否合理，通过验证因子分析，来对测试题目进行检验。通过检测，KMO值是0.627，超过了0.5，且显著性为0.000，小于0.05，说明数据适合进行因子分析。

初中生计算思维发展现状分析

1.调研对象基本情况

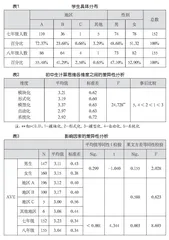
本次研究调查集中向3个地区的七、八年级的学生发放问卷，其中七年级回收152份问卷，八年级回收155份问卷。学生具体分布如下页表1所示。

通过分析表1可以得出，A地区共196人，占比63.84%，B地区共100人，占比32.57%，C地区共5人，占比1.64%，其他地区共6人，占比1.95%，所以有超过一半的学生来自A地区。男生共147人，占比47.9%，女生共160人，占比52.1%，不论是七年级还是八年级回收的问卷，女生的比例均要比男生高。

2.初中生计算思维发展现状及影响因素分析

（1）初中生计算思维发展现状分析

研究对象测试得分的总体平均分为15.66分，满分为20分，表明初中生计算思维总体发展水平较为优秀，说明初中生在计算思维方面已经具备了一定的基础和能力。此外，本研究对研究对象从五个指标维度进行差异性分析，结果如表2所示。

通过表2可以看出，组间的F值为24.728，且显著性＜0.01，说明初中生计算思维发展水平在不同维度之间存在显著差异。使用事后比较的方法进一步进行比较，发现初中生计算思维的发展在自动化和系统化水平之间的差异不显著，但二者水平显著低于其他三个维度的水平，此外，模型化发展水平显著高于其他维度发展水平。

（2）初中生计算思维发展影响因素分析

如表3所示，在深入分析研究对象的自然属性因素（性别、地区）和课程属性因素（年级）时，采用独立样本t检验和方差分析进行了差异性分析。就性别而言，莱文方差等同性检验中p=0.155＞0.05，说明不同性别的学生得分方差相等，平均值等同性t检验中显著性p=0.299＞0.05，意味着不同性别的学生得分差异不具有显著的统计学意义。对于地区因素，方差分析中显著性为p=0.588＞0.05，说明来自不同地区的学生计算思维得分情况不存在显著性差异。因此，研究对象的自然属性因素对初中生计算思维的发展不存在影响。在年级方面，莱文方差等同性检验中p=0.003＜0.05，说明不同性别的学生得分方差不相等，平均值等同性t检验中显著性p＜0.05，意味着不同年级的学生得分差异具有显著的统计学意义。因此，课程属性因素，即不同年级的教学内容会影响初中生计算思维的发展。

如表4所示，对研究对象的发展属性因素进行相关性分析。可以看出，五个维度两两之间的相关都具有显著统计意义（p＜0.01或p＜0.05），且均为正相关关系，说明不同维度在初中生计算思维的发展过程中不是孤立的，而是相互关联、相互影响的。因此，在教学过程中，教师应注重这些维度之间的联系和整合，从而更好地培养学生的计算思维能力和创造力。

3.结论

（1）初中生不同年级计算思维水平存在显著性差异

七年级的课程内容旨在夯实基础，注重逻辑编程和数据处理的初步训练，而学生初涉信息科技，其计算思维尚显稚嫩。但在解决问题的过程中，学生们开始尝试将复杂问题拆解为更小、更易于处理的部分，这标志着计算思维中模块化初步萌芽。然而，他们在运用规范化语言和符号来描述问题时仍面临挑战，形式化表达能力有待提升。

进入八年级，课程内容逐渐深化，触及算法、数据结构和面向对象编程等领域。学生们在计算思维上取得显著进步，开始运用抽象模型来分析和解决问题，模型化能力显著增强。并且随着对编程的深入理解，他们开始意识到自动化的价值，并尝试利用计算机技术实现自动化任务，展现了计算思维的进阶应用。

（2）初中生计算思维模型化发展水平较高

初中生计算思维模型化发展水平较高。这主要得益于他们所处的青春期的特质，他们对新事物充满好奇与渴望，对计算机编程等技术怀有浓厚兴趣，这种强烈的好奇心与求知欲促使其在学习计算思维时更为投入，进而提升了模型化水平。同时，随着认知能力的逐渐成熟，他们能够理解和掌握较为复杂的逻辑关系和抽象概念，在计算思维的学习过程中，能够较好地将现实生活中的问题抽象成数学模型，从而进行求解。此外，越来越多的学校开始重视计算思维的培养，开设了编程、机器人等课程，这些课程为学生提供了实践操作的机会，使他们在实践中不断提高模型化水平。

（3）初中生计算思维自动化和系统化发展水平较低

初中生计算思维自动化和系统化发展水平较低。首要原因是，初中生处于思维发展的关键阶段，他们的逻辑思维和抽象思维能力还在形成中，对复杂的概念和系统可能还无法完全理解和掌握，这导致他们在计算思维自动化和系统化方面存在一定的困难。其次，当前的初中教育体系在计算思维培养方面仍有待加强，虽然许多学校已经开始重视计算思维的教学，但整体上，相关课程设置和教学资源仍然有限，无法满足学生全面发展的需求。此外，由于初中生处于青春期，部分学生可能存在注意力不集中、自我管理能力较弱等问题，这也影响了他们在计算思维自动化和系统化方面的学习效果。

初中生计算思维培养建议

1.分阶段针对性教学

面对初中生不同年级计算思维水平存在的显著性差异，可以采用分阶段且有针对性的教学方法。首先，设计分阶段的进阶课程，确保学生在掌握前一阶段所学内容的基础上，逐渐过渡到下一阶段的学习。这样既能保证学生的学习效果，又能避免因难度跨度过大而影响学生的学习积极性。其次，针对不同年级的学生，制订差异化的教学计划。对于七年级学生来说，应重点夯实基础，通过有趣的编程实例和实践活动，引导学生理解计算思维的基本概念，如模块化思维。同时，注重培养学生的形式化表达能力，通过练习使用规范化语言和符号描述问题，逐步提高其思维严谨性。而八年级学生则可以更加注重复杂问题解决和系统化思维的培养。通过项目驱动的教学方式，培养学生的抽象思维和模型化能力。鼓励他们利用计算机技术解决实际问题，提高计算思维的实践应用能力。