小学高年级学生计算思维影响因素及提升路径研究

摘要：本研究选取K市四所小学五、六年级中的344名学生为研究对象，对小学高年级学生的计算思维水平进行描述性、差异性、相关性和回归分析，并通过结构方程模型（SEM）挖掘小学高年级学生计算思维水平的影响因素。研究结果表明：K市小学高年级学生计算思维水平整体良好；不同性别，五、六年级之间，互联网使用频率和学习信息技术课程的态度对计算思维水平没有显著的影响；互联网使用态度、编程经验、信息技术课程内容、数学成绩和科学成绩与计算思维水平之间存在显著正向相关关系。最后，本研究依据数据分析结果提出了促进小学高年级学生计算思维发展的建议。

关键词：小学高年级学生；计算思维；现状；影响因素

中图分类号：G434  文献标识码：A  论文编号：1674-2117（2024）14-0032-07

随着数智时代的到来，计算思维这一概念应运而生，被认为是一项“人人都应该具备的态度与技能”。[1]欧美、澳大利亚、新加坡等国家和地区都将计算思维培养纳入K12阶段的人才培养计划[2]，

我国《义务教育信息科技课程标准（2022年版）》（以下简称“新课标”）中将计算思维划定为信息技术学科的四大核心素养之一。[3]可见，计算思维培养的对象趋于“低龄化”。小学高年级学生具备一定的知识和认知基础，处于计算思维培养的关键期。然而，目前对哪些因素影响着小学生计算思维能力的相关研究较少。基于此，本研究采用问卷调查法分析K市小学高年级学生计算思维水平的现状，深度挖掘并分析其影响因素，探究各因素与计算思维间的关系，力求为小学高年级学生的计算思维能力培养提供有价值的参考。

概念阐述与问题提出

1.计算思维概念界定

计算思维的概念最早于2006年由卡梅隆大学的周以真教授提出，即计算思维是运用计算机科学的基础概念来解决问题、设计系统和理解人类行为的过程[4]，2011年周以真教授进一步将计算思维的概念总结为一个能够被信息处理主体有效执行的思维过程[5]，由此可以看出计算思维的概念经历了从重操作技能到重思维过程的转变。之后，国内外更多学者加入到对计算思维的研究中，如美国国际教育技术协会（ISTE）2015年提出：计算思维是能够有效结合数字技术与人类思想，解决复杂现实问题的一系列心智工具集。[5]新课标指出，计算思维是指个体运用计算科学领域的思想方法，在问题解决的过程中涉及的抽象、分解、建模、算法等思维活动。[3]

2.影响计算思维水平的因素

从个体固有属性看，年级和性别是首先应该考虑的两个变量，已有研究对上述两个因素对计算思维的影响有着相互矛盾的结论，如苏梅拉、阿特马兹杜（Atmatzidou，Soumela）[6]等人指出年级和性别与计算思维没有显著相关性，而克鲁斯（Crews）[7]等人提出女生取得与男生相当的计算思维水平需投入更多的时间，说明年级和性别是否影响计算思维水平仍没有定论。

从外部因素看，随着互联网的普及与发展，学生使用互联网进行学习、娱乐和交际等，互联网使用态度和频率也会对学生问题解决的思维过程产生影响；编程学习对学生抽象、算法思维能力的发展起到了一定的作用，所以编程基础可能会成为学生计算思维水平的影响因素；小学信息技术课程是培养学生计算思维能力的重要学科，所以学生对信息技术课程的满意度以及课程的新颖度可能也是影响计算思维水平的因素[8]；数学、科学等学科也是以问题解决为核心，在学生学习的过程中其计算思维水平也会产生变化，而已有研究较少跨学科对计算思维能力的影响进行探究。

综上所述，本研究拟探究年级、性别、互联网使用态度和频率、编程经验、信息技术课程态度和内容以及数学和科学成绩对计算思维水平的影响。

研究设计与过程

1.研究工具

在本研究中，计算思维水平评测部分采用张屹[9]等人开发的“小学生计算思维量表”，量表共计23个项目，可在编程与非编程环境下开展，同时，为了更符合高年级小学生的阅读习惯，本研究对该量表部分题项的语言表述加以优化。从信度来看，量表总体的克隆巴哈阿尔法（Cronbach’s Alpha）信度系数和折半信度系数分别为0.890和0.858，均大于0.8，表明该量表具有较高的信度；从效度来看，量表KMO值为0.896，表明各题项间存在较强的相关性，问卷效度较好。计算思维影响因素部分，分别采用无序分类型变量记录被试的年级和性别，以及有序分类型变量调研被试的互联网使用态度和频率、编程经验、信息技术课程态度和内容、数学成绩和科学成绩。其中，态度采用李克特五点式从消极到积极分别赋分1～5分，频率和编程经验按时间的长短进行赋分，成绩按区间范围内从低到高进行赋分。

2.被试选择

为使调研数据具有比较好的层次覆盖度，本研究选择K市四所小学，随机抽取了360名五年级和六年级的学生作为研究对象，向他们分发了360份调查问卷，并成功回收了全部360份，回收率达100%。其中，有16份问卷被认定为无效，因此有效问卷数量为344份，有效回收率为95.5%。研究对象包括了179名五年级学生（占比52%）和165名六年级学生（占比48%），性别分布为男生169人（占比49.1%），女生175人（占比50.9%）。

3.数据处理

计算思维自评量表采用李克特式五级分布，即从完全不符合到非常符合，分别赋值1～5分，量表共23个题，总分115分，为便于研究，将计算思维总体得分转换为百分制计分（计算方法为：实际得分/115*100），低于60分为不及格，60～79分为及格，80～89分为良好，90～100分为优秀。所得数据采用SPSS 27.0进行描述性统计、差异性、相关性和多层回归分析，并使用Amos 26.0软件构建结构方程模型解释和预测各因素对计算思维水平的影响关系，以进一步建构各因素与计算思维发展的关系模型。

研究结果

1.计算思维水平的描述性统计分析

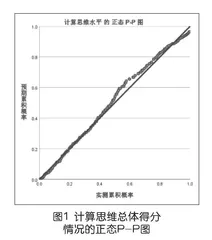
在整体样本中，小学高年级学生计算思维得分最低分为46.33分，最高分为98.67分，均值为79.88分（SD=10.321）。从下页图1正态P-P图中可以看出，样本数据得分情况不完全符合正态分布，所以选择中位数（80.83）代表整体情况，中位数表明所采集样本群体的计算思维水平良好，但仍具有上升空间。下页图2直方图显示，在样本数据中，大多数学生计算思维得分处于75～85分，高于60分的及格线。

小学高年级学生计算思维能力量表采用李克特五点计分法，其理论中间值为3。经过统计学分析，总体样本数据的计算思维能力均分为3.99＞3（如表1），小学高年级学生整体计算思维能力呈中等偏上的位置。由表1可知，计算思维五个维度的因子水平表现为：创造力＞批判思维＞合作能力＞问题解决能力＞算法思维。其中，创造力、批判思维、问题解决能力、算法思维维度和总体得分呈左偏平峰分布，均值作为集中趋势的代表存在低估；合作能力维度得分呈右偏平峰分布，因此均值作为合作能力维度得分存在高估趋势，且总体离散趋势较弱。

2.计算思维水平的差异性分析

（1）独立样本T检验

学生的计算思维水平可能会受到个体因素的影响，采用独立样本T来比较年级和性别（二分变量）在计算思维水平上的差异。从年级分布上看，五年级学生的计算思维总体水平（M=78.97±10.32）略低于六年级学生（M=80.85±10.28），但差异不显著（t=-1.68，p=0.093），在各子维度上，六年级学生的创造力显著高于五年级学生（t=-2.10，

p=0.037）；从性别方面看，男生（M=79.90±10.65）与女生（M=79.85±10.03）的计算思维总体水平的差异较小，且这种差异不显著（t=0.048，p=0.96），在各子维度上也未呈现显著差异。

（2）单因素方差分析

对互联网使用态度和频率、编程经验、信息技术课程态度和内容、数学成绩和科学成绩（大于等于三分变量）这五项影响因素进行单因素ANOVA检验。样本数据中不同互联网学习态度（F=5.15，p=0.002）、编程经验（F=3.13，p=0.004）、信息技术课程态度（F=3.59，p=0.007）、信息技术课程内容（F=6.12，p＜0.001）、数学成绩（F=9.73，p＜0.001）和科学成绩（F=9.26，p＜0.001）的学生在计算思维水平方面得分差异显著。

其中，在互联网学习态度中，认为利用互联网进行学习一般重要（M=77.47±10.74）的学生，计算思维水平显著低于互联网学习态度为比较重要（M=80.71±10.11）和非常重要（M=82.92±8.23）的学生。

在编程经验中，通过不同方式学习编程课程大于两年（M=81.79±17.64）的学生，计算思维水平显著高于没有接触过编程课程的学生（M=72.89±15.37）。

针对信息技术课程，非常喜欢课程（M=81.20±10.60）的学生，其计算思维水平显著高于不喜欢课程（M=76.10±14.31）的学生，认为信息技术课程内容没有吸引性、更新滞后的（M=75.92±11.17）学生，其计算思维水平显著低于认为课程内容有趣和更新及时（M=82.25±9.69）的学生。

在学业成绩方面，近一次数学考试成绩高于90分（M=82.75±10.04）的学生，其计算思维水平显著高于其他任意分数段的学生，如70～80分（M=72.87±8.30），近一次科学考试成绩高于90分的学生（M=81.79±10.18），其计算思维水平显著高于分数为60～70分（M=70.99±10.33）和70～80分（M=77.14±9.48）的学生。

（3）各变量与计算思维水平的相关性分析

计算思维水平可能的影响因素为分类型变量，计算思维总体得分为连续数值型变量，探索两种变量间的相关性采用斯皮尔曼系数。分析结果如表2所示，在样本数据中，性别、互联网使用频率与学生的计算思维水平并未呈现显著的相关关系，而年级、编程经验、互联网学习态度、信息技术课程态度与内容、数学和科学成绩与计算思维水平显著相关。相关系数r值在小（r=0.107）到中等（r=0.329）程度范围内变化，且与计算思维存在相关性的各变量的r值均大于0，表明变量与计算思维水平存在正向的线性相关关系。

（4）各变量与计算思维水平的多层回归分析

在进行了相关性分析后，为进一步探究各变量与计算思维水平之间的因果关系，需进行回归分析，以明确计算思维水平的影响因素。由相关性分析结果可知，年级和互联网使用频率与计算思维水平之间没有显著相关关系，所以将上述两个因素作为控制变量，其他可能的影响因素作为核心自变量，多层回归分析结果如上页表3所示。模型1是控制变量（性别和互联网学习频率）对因变量（计算思维水平）的影响，模型2是在控制变量的基础上加入了核心自变量对因变量的影响。模型2的F值为9.060，在p＜0.001的水平上显著，证明模型2的构建有效，多层回归分析结果进一步证实了互联网学习态度（β=1.928，p＜0.01）、编程经验（β=1.827，p＜0.01）、信息技术课程内容（β=2.159，p＜0.001）、数学成绩（β=2.362，p＜0.001）、科学成绩（β=1.830，p＜0.001）对计算思维水平存在正向影响。但是，性别，五、六年级两个年级之间，互联网使用频率，信息技术课程态度对计算思维水平不存在显著的影响关系。

（5）结构方程模型（SEM）的构建与分析

利用Amos构建结构方程模型进行检验，可以通过路径系数揭示变量之间的结构关系。[8]首先进行模型拟合指数检验，结果如表4所示，对比标准值，显示该模型的拟合度良好。