基于计算思维框架的编程教学模式探索与实践

摘要：在信息技术课堂上，教师大多通过编程来实现对学生计算思维能力的培养，然而在传统的“讲授-练习”教学模式下，对学生思维方式的培养是很抽象的，没有具体化的思维活动。因此，作者提出基于计算思维框架的编程教学模式，将计算思维的要素与教学活动联系起来，并具体化为一系列在教学活动中可实施的思维活动，从而完成对学生计算思维能力的培养。

关键词：信息技术；计算思维；教学模式

中图分类号：G434  文献标识码：A  论文编号：1674-2117（2022）21-0037-03

《普通高中信息技术课程标准（2017年版）》（以下简称“新课标”）在学科核心素养中对学生的计算思维提出了要求。通过计算思维的培养，学生可以掌握如何分析新信息和处理新问题。现阶段，信息技术课堂对学生计算思维的培养大多通过开设编程课来实现，在课堂上学生能够运用编程语言解决问题被认为是有效的计算思维的培养，但编程要做的绝不仅仅是对学生进行技术训练，而是要关注如何让学生理解和掌握编程背后用到的思维的过程。笔者结合新课标对计算思维框架的定义与要求，提出了基于计算思维框架的编程教学模式，在信息技术编程课堂上指导学生运用计算思维框架来思考问题，从而有效引导并培养学生的计算思维能力。下面，结合具体案例展示如何使用计算思维框架进行编程教学。

计算思维框架的要素及其含义

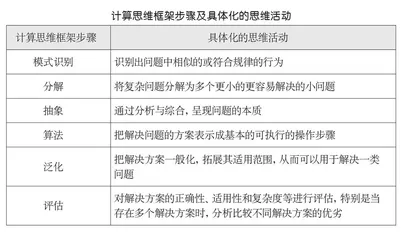
新课标在对计算思维的定义中，明确计算思维的要素主要包括抽象、分解、算法、模式识别、泛化和评估，笔者基于六要素提出了基于计算思维框架的编程教学模式，将计算思维的六要素以具体化的思维活动贯穿于课堂教学活动中，从而完成对学生计算思维能力的培养。下表展示了计算思维框架的步骤及每个步骤被具体化的思维活动。

基于计算思维框架的编程教学模式实施

结合提出的计算思维框架，笔者以《for循环打印字符图形》为例，以难度递进的四个任务为主线，运用计算思维框架，探索信息技术编程课堂中基于计算思维框架的编程教学模式的具体实施。

任务一：编程输出n行m列的*号矩形。当n=5，m=8时，输出如图1所示的图形。

对于图1所示的矩形，引导学生运用计算思维的6个步骤来分析，实现过程如下（以n=5，m=8为例）。

模式识别——输出的矩形中存在重复的模式，每行作为一个整体，那么问题就变成了输出一行*号，并重复5次（如图2）。

分解——输出一行*号还是无法直接用输出语句实现，本例中输出一行8个*号可以分解成输出一个*号不换行，此动作重复8次。

抽象——经过前面两步，问题可以抽象成：①输出一个*号不换行，重复8次；②输出一行*号重复5次。

算法——基于上述分析，可以得出一个步骤列表：①输入行号n和列号m；②重复执行抽象、算法步骤n次；③重复执行输出*号m次不换行；④换行。

泛化——如果将本题进行变换，输出其他的图形或者数字，上述思想同样适用。因此，我们可以将问题进行抽象，用于解决输出相同形状的符号矩形问题。

评估——上述算法可以简洁有效地解决输出*号矩形的问题，并且有很强的复用性，类似输出字符图形的问题都可以用此模板来解决。

在完成任务一的基础上，将任务一进行变换，实现输出图1所示的*号直角三角形。学生仍然运用计算思维框架来分析完成。在课堂实施过程中，学生快速地完成了模式识别这一步骤。在分解这一步骤，由于每行做的事情仍然是重复输出一个*号，不同点在于每行输出的*号个数不同，因此重复次数不同。引导学生观察每行*号个数的出现规律，第一行1个*号，第二行2个*号……第五行5个*号，可以得出结论每行的*号数与行数相同，因此抽象出每行*号重复次数与行数相等。基于上述分析，学生很容易地完成了算法过程，并能快速编程实现。

进一步给出输出图1所示*号平行四边形的任务。平行四边形和前面图形的区别在于需要在输出*号前输出空格，因此存在相同的模式即每行先输出空格再输出*号。在分解阶段，将每行输出内容分解为先输出空格不换行，重复若干次，再输出*号不换行，重复5次。学生观察空格规律得出每行输出的空格数为行数减一。基于以上分析，问题可以抽象为输出一个空格不换行，重复次数为行数减一次，紧接着输出一个*号不换行，重复5次。将上面的操作重复行数次即可实现输出*号平行四边形。

经过运用计算思维框架完成三个图形的输出任务后，学生对计算思维的一系列思维活动有了清晰的认知，能够较为熟练地运用计算思维框架去思考并解决问题。因此在课程最后，抛出一个与前面的任务有关联但是有难度跨度的问题，即编程输出如下页图3所示的乘法口诀表。

输出九九乘法表的计算思维过程如下。

模式识别——此图存在重复的模式，每行输出和行数相同个数的等式。每行中等式的第一个乘数是递增的，第二个乘数相同。

分解——具体分析每一个等式，可以分解为先输出第一个乘数，输出x号，输出第二个乘数，输出等号，最后输出两个数的乘积。

抽象——观察可得，每一行等式的第一个乘数从1变化到行数n，第二个乘数和行数n相等。因此问题可抽象为：①每行输出行数个等式；②每个等式表示为i*j=res，其中i表示当前行的第几个等式，j表示当前的行数，res表示i乘以j的乘积。

算法——基于上述的分析，可得出算法如下：①重复执行步骤[2]9次；②重复执行抽象步骤j次（j∈（1，9））；③输出i*j=res，输出空格不换行（i∈（1，j））；④换行。

泛化——如果将本题进行变换，输出有规律变化的式子，上述思想同样适用。因此，我们可以将问题进行抽象，用于解决有规律变化的式子输出问题。

评估——上述算法可以简洁高效地解决输出乘法表的问题，并且有很强的复用性，类似输出有规律变化的式子问题都可以用此模板来解决。

教学模式对比实验

在实际课堂实施中，笔者选取四个班级，将本文中的教学任务按照传统教学模式和基于计算思维框架的教学模式两种方式展开对比教学实验。传统教学模式指按照常规的教学方法即老师讲解解题思路，学生编程实现；基于计算思维框架的教学模式在课堂中要求学生首先按照计算思维的六个步骤进行思考，完成思维活动后再编程实现。A1、A2两个班级运用传统教学模式完成教学，B1、B2两个班级运用基于计算思维框架的教学模式展开。对比两种教学模式在教学过程中学生对四个任务（输出星号矩形T1、星号三角形T2、星号平行四边形T3、乘法表T4）的初始完成率c_1和最终完成率c_2。其中，初始完成率c_1是指教师没有讲解题目前学生独立思考编写的程序能够通过OJ系统评测的占所有学生的比值;最终完成率c_2是指在传统教学模式下教师讲解解题思路后学生的题目提交通过率和基于计算思维框架教学模式下教师带领学生按照计；算思维框架的六个步骤完成思维活动后，学生的题目提交通过率。

在实验结束后，笔者根据学生的初始完成率c_1和最终完成率c_2统计数据分析得出：对于T1和T2两道题，在传统教学模式下学生的题目初始完成率和基于计算思维框架的教学模式没有明显的差别，而T3和T4两道题，使用基于计算思维框架的教学模式的初始完成率要高于传统教学模式。分析其原因在于，T1是本堂课的第一个任务，在教师没有讲解之前，初始完成率是四个班级学生的真实水平的反映，而T2作为第二个任务，学生对计算思维框架理解还不够透彻，因此计算思维框架对其思维活动的帮助还没有显现。随着学生对计算思维框架的不断熟悉，对计算思维框架的一系列思维活动的深入理解，学生在完成T3和T4两道题时，已经可以很好地应用计算思维框架帮助自己一步步分析问题，根据计算思维的一系列思维活动将复杂问题分解为可以具体化的小问题，从而编程实现。

结语

通过以上分析可以看出，学生运用计算思维框架的六个步骤来思考问题，能够帮助他们将遇到的复杂问题分析简化成更容易解决的小问题，从而完成对问题的求解。在信息技术编程课堂上通过具体化的思维活动来培养学生的计算思维，可以帮助学生养成自主思考、尝试多角度解决复杂问题甚至提出新问题的能力。

参考文献：

[1]曹杨璐，谢忠新.信息技术学科计算思维的迁移能力培养实践研究[J].信息技术教学，2021（15）：54-57+100.

[2]李锋，王吉庆.计算思维：信息技术课程的一种内在价值[J].中国电化教育，2013（08）：19-23.