基于核心素养的初中数学“综合与实践”教学设计研究

[摘要]核心素养的提出推动了我国素质教育的改革。发展学生的核心素养重点在于培养学生的学科核心素养。数学“综合与实践”课程内容具有综合性和实践性的特征，有利于培养学生的数学核心素养。研究以“泰森多边形”教学设计为例，按照“发现问题、提出问题、分析问题、解决问题”的思路展开教学设计，将教学和学生数学核心素养有效结合，阐述了基于核心素养的初中数学“综合与实践”教学设计的基本策略，为一线初中数学教师提供案例参考。

[关键词]数学核心素养;“综合与实践”;初中数学;教学设计

[中图分类号]G632[文献标识码]A[文章编号]1005-5843（2022）05-0024-06

[DOI]10.13980/j.cnki.xdjykx.2022.05.005

一、问题的提出

随着教育改革的不断推进，我国基础教育从“知识本位”时代逐渐过渡到“核心素养”时代，核心素养的落实问题逐渐引起教育研究者和一线教师的重视。有学者在文献综述的基础上提出研究数学素养的4个落脚点，强调了要分析探索数学素养生成的教学策略[1]。还有学者提出“学科知识是学科核心素养形成的主载体，学科活动是学科核心素养形成的主路径”[2]。由此可见，数学核心素养的研究应当在实际教学中进行，在教学设计中探究出数学核心素养在课堂的落脚点、生长点和发展点的一般规律。因此，基于数学核心素养进行教学设计，根据具体的教学内容、教学情境落实数学核心素养是亟待解决的重要问题。

二、“综合与实践”是数学核心素养落地生根的沃土

（一）“综合与实践”是课程的重要组成部分

2001年7月，教育部在《全日制义务教育数学课程标准（实验稿）》中首次指出将“实践与综合应用”纳入到义务教育数学课程中[3]。2011年12月，《义务教育数学课程标准（2011年版）》将“实践与综合应用”独立成一个新的板块，即“综合与实践”，并阐明其概念以及设置目的[4]。2022年4月，《义务教育数学课程标准（2022年版）》要求各学科增加10%的课时进行跨学科主题学习活动[5]。新课标对综合实践课时的规定进一步提高了数学综合实践的地位，使之成为课程的重要组成部分，同时跨学科教学模式也被重视起来。但是教科书中的“综合与实践”课题数量有限，需要教师自主开发基于核心素养、符合学情和学科特点的“综合与实践”活动。

（二）基于核心素养的“综合与实践”是综合型人才培养的载体

国家推行基础教育改革，积极倡导素质教育，以期培养适应社会发展的综合型人才。“综合与实践”课程强调让学生在亲身体验学习的过程中提升知识、丰富经验，综合运用多种学科知识去完成特定的活动或解决特定的问题，有助于培养学生的核心素养，提升多元学科知识融合的能力和创新能力，使学生逐步成长为适应社会发展的综合型人才。

（三）基于核心素养的“综合与实践”教学设计与实施是提升学生核心素养的有效路径

培养全面和谐发展的人是教育者和社会共同的目标。马云鹏教授认为，数学核心素养可以理解为学生学习数学应当达成的有特定意义的综合性能力[6]。史宁中、孔凡哲两位教授认为，数学核心素养是学生亲身自主经历和体验数学化的活动进而所积淀和升华的产物，这种产物对学生在数学上全面、和谐、可持续发展起决定作用[7]。基于核心素养的“综合与实践”教学设计与实施是提升学生核心素养的有效路径。笔者所任教的学校——东北师范大学附属中学一直倡导着生命教育，将“涵育素养，立德树人”作为教育教学的目标，教师们共同研究如何在实际课堂中落实立德树人，培养学生的核心素养，构建初中数学“综合与实践”课程的教学设计原则和策略，以期培养学生数学核心素养，为学生终身学习奠定基础，为初中数学“综合与实践”课程内容体现其应有的数学教育价值提供保证。

本研究就以笔者在本校第35届教学“百花奖”中所教授的“泰森多边形”为例，阐述基于核心素养的初中数学“综合与实践”教学设计的基本原则与策略，论证揭示数学核心素养的课堂落脚点、生长点和发展点，为一线初中数学教师提供案例参考。

三、基于数学核心素养的初中数学“综合与实践”教学设计与实施

（一）对标核心素养，解析教学内容

“泰森多边形”是在数学综合实践活动中被提炼得非常好的素材之一。“泰森多边形”是数学的一个瑰宝，以初中数学知识为基础，其应用极其广泛，能够体现数学的建模过程，在解决问题中可涉及很多学科知识，具有开发价值。本课例涉及的基础知识是八年级几何部分的线段垂直平分线，非常基础，学生也比较熟悉，运用线段垂直平分线构造的数学模型——“泰森多边形”可解决很多最优问题。为了能够提高大面积气象预报的准确度，荷兰气象学家A.H.Thiessen想对气象观测站进行有效区域划分，然后根据离散分布的气象站的降雨量计算平均降雨量。他将所有相邻气象站连成三角形，作这些三角形各边的垂直平分线，用每个气象站周围的若干条垂直平分线围成多边形。再用这个多边形内所包含的一个唯一气象站的降雨强度表示这个多边形区域内的降雨强度，并称这个多边形为“泰森多边形”。“泰森多边形”的应用原理包含了线段垂直平分线的作图方法、性质、多边形的分割等知识，“泰森多边形”的应用体现了对数学基本原理的学习方法和依据数学原理建立数学模型解决实际问题的思考，泰森多边形也体现了数学之美。

本课例的教学重点首先是实际问题数学化，其次是运用垂直平分线性质，逐步实现多点平面区域的划分，经历和体验用数学方法解决实际问题的一般思路。

（二）分解核心素养，设置教学目标

依据中学数学教学设计理论，在学生的培养目标上强调三维目标的整合，最终实现数学素养的达成和促进学生核心素养发展的目标。因此，在进行目标设计时，应注重有效结合各内容的目标，避免教学目标出现“为了综合而综合”的情形;要注重分析关于“综合运用”的具体表述，将过程与方法细化。在进行情感态度与价值观目标分析时，应从学生的学习兴趣、参与程度、体验性以及主体性上考虑。依据“综合与实践”课程内容的实践性，目标应该具有针对性和现实性。针对性要求目标的分析应该是具体的、微观的，现实性要求一定是当下的课程中发生的和形成的学生对于数学的情感。

例如本课例的教学目标设置如下：针对“划分急救站的最佳服务范围”问题，学生能多角度分析影响因素，将复杂情境进行抽离，抽象出数学问题，感悟如何从数学的角度发现问题和提出问题;学生运用线段垂直平分线性质，能解释“最佳服务范围”划分的方法，并能用数学语言进行交流和展示，感悟“重事实、讲道理”的科学精神;学生通过自主思考、合作交流，综合分析问题，逐步积累数学活动经验，体会从简单到复杂、从特殊到一般的数学研究方法，以及用数学方法解决实际问题的一般思路。

（三）基于核心素养，选择教学策略

林崇德教授指出，课程改革、教学实践和教育评价是落实核心素养的途径。显然通过课程改革的途径落实数学核心素养的任务是非常艰巨的。因此，研究试图从教学实践和教育评价方面探索基于核心素养的初中数学“综合与实践”的教学策略。本课例从学生的最近发展区设置问题，引导学生采用自主探究与合作交流相结合的方式进行学习，调动学生学习的积极性和主动性，使学生的核心素养在实际问题探究与解决的过程中得以培养。

1.创设问题情境，激发学生学习兴趣。有效培养学生的数学核心素养，就要求教师在实际教学过程中，应着重考虑具体的核心素养和具体情境的相关性[8]。以“急救站最佳服务范围的划分问题”为背景，引发学生的认知冲突，让学生意识到研究不等关系的关键在于研究等量关系，将未知的问题转化成已有的知识能够解决的问题，为“泰森多边形”的引出提供先行组织基础。

2.抓住核心知识，引导学生举一反三。本课例的综合性比较强，难度很大，学生对于不等关系的研究容易在认知上出现问题。引出在整个探究过程中始终围绕线段垂直平分线展开，将多点问题转化成两点问题，始终体现从特殊到一般的研究思路。因此，本课例在问题探究的过程中牢牢抓住数学核心概念——线段垂直平分线，体现线段垂直平分线性质的应用价值。

3.设置问题清单，引领学生深度思考。 “综合与实践”的实践性与综合性强，在教学方法和学习方式上都与基础的数学知识学习不同。问题驱动式的教学模式有助于学生学习，但问题设置不能够限制学生思维。在教学设计的过程中要选择合适的现实背景，设置既开放又有引领作用的问题串，注重在问题解决过程中综合运用数学知识，既能让学生体验运用数学知识解决实际问题的过程，积累运用数学知识的经验，又能提升学生分析、解决问题的能力。例如设置“问题清单”，让学生根据所学知识记录提出问题：“（1）根据问题背景和作图方法，我提出的问题如下……;（2）我们小组能够解决的问题……;（3）我们小组发现泰森多边形的性质……”在问题驱动下，引导学生进行元认知，深度思考，增强学生应用数学知识解决实际问题的意识和能力，真正体现“综合与实践”课程培养学生核心素养的教育效果。

4.提供多元评价，培养学生核心素养。喻平教授基于知识理解、知识迁移和知识创新3种水平建立了数学核心素养评价框架，该评价框架对基于数学核心素养的教学评价具有指导意义[9]。笔者认为“综合与实践”的教学评价要兼顾学生与教师、兼顾自评与互评、兼顾数学核心素养。笔者与同事们共同设计了“综合与实践”教学评价量表，既可以兼顾教师和学生，又可以兼顾自评与互评;既能兼顾数学核心素养，把学生数学核心素养的达成作为评价的元素，又能关注学生参与活动的态度，有助于教师诊断学生存在的问题;既重视过程评价，把学生之间的合作、学生的活动过程等作为评价的对象，又注重个性化评价，指向每一位学生，促使教师可以根据评价的结果有针对性地指导学生以便因材施教。

本课例采用“综合与实践”课程的教学评价量表，提供了多元评价方式。课上分小组进行，成果展示与交流，在各组代表作研究报告的基础上，可以根据情况选择纸笔测试、作品评分表、表现评分表、任务完成表和自我反思表等进行评价。学生与教师一起进行，全班通过质疑、辩论、评价，总结成果、分享体会、分析不足，开展自我评价、同学评价和教师评价，完成本次综合与实践活动。

（四）精设教学过程，落实核心素养

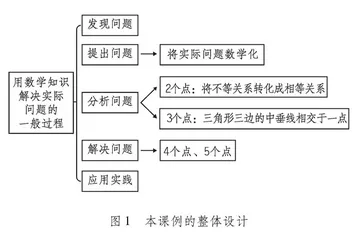
本课例遵循着综合实践的研究规律，关注知识的应用原理，为学生设计了完整的实践过程，希望学生通过学习不仅获得知识技能的积累，更能获得经验积累，尤其是对数学研究与应用的学习和体验。因此，本课例的素材选自线段垂直平分线，因为线段垂直平分线是尺规作图的重点和研究轴对称的基础，对垂直平分线作图的理解和操作步骤的掌握是后续几何学习不可或缺的能力。本课例力争通过综合实践让学生体会数学知识的应用，激发学生的创新精神，开拓学生视野，让学生在实际情境中经历发现问题、提出问题、分析问题、解决问题并应用于实践这一完整过程，让所学知识通过活动的形式得以延伸和应用（本课例的整体设计见图1）。

为了较好地落实本课例的预期教学，现将这节充斥着理性逻辑光华的综合实践课拆分成以下5个核心部分。

1.创设情境，激发兴趣。基于情境认知学习理论，应让知识从情境体现，在情境互动的过程中进行动态学习，激发学生的社会责任感。同时，实际问题数学化也是本节课学生学习中的难点之一，通过教师的引导使学生学会运用数学语言描述世界，能够让课堂教学富有生活特色。另外，总结出用数学知识解决实际问题的一般过程，即“发现问题——提出问题——分析问题——解决问题——实际应用”，整体上为“泰森多边形”的学习提供一条路线图。

教师在上课前可以先让学生观看“长春急救中心宣传片”，让学生变身为“长春120调度指挥中心的调度员”，思考当接到求救电话后如何快速选择急救站，并派出急救团队。通过学生讨论，要想让救护团队最快到达求救地点，学生将考虑到影响决定的最重要因素是急救站与求救者位置之间的距离。为解决问题，教师将问题引导为划分急救站的最佳服务范围，并引导学生将实际问题转化为数学问题，用数学语言描述问题。

2.分析问题，感悟新知。教师引导学生在解决复杂问题时可以从简单到复杂，化繁为简，因此要解决5个控制点的问题，可以从2个、3个、4个控制点逐一考虑;通过不会划分多个急救站的服务范围引发认知冲突，从而形成引入“泰森多边形”必要性的认识;用分类讨论的思想逐一研究每对关系，进而解决问题;通过介绍“泰森多边形”的相关科学史，让学生在学习数学知识的同时了解更多的科学文化。