巧用比较策略，突破学生的学习难点

【摘 要】在小学数学课堂教学中，学生往往会遇到一些难点问题，这些难点的产生有的是因为相似内容的互相混淆，有的是因为学习内容的互相迁移，还有的是因为知识点的螺旋递进等。本文根据教学实践，阐述教师如何巧妙运用比较策略，帮助学生建立知识的联系和区别，提高数学课堂教学效率。

【关键词】数学教学 比较策略 课堂难点

在数学课堂教学中，学生对抽象概念的理解有一定困难，如相似的知识内容、知识点的螺旋递进、知识点的负向迁移等因素。为此，教师往往会选择大量的习题，希望学生通过不断地练习突破这些难点。然而事与愿违，大量的练习不仅让学生产生了逆反心理，而且大大降低了学生对数学学习的兴趣。笔者认为，要帮助学生突破学习的难点，就需要运用比较策略，带领学生整合知识之间的区别和联系，突破学习难点，提高课堂教学的实效性。

一、运用比较策略，串联相近知识

在小学阶段学习的内容中，有一些相近的知识，由于比较零散，不能形成一个完整的知识链，学生学起来容易犯错误。

如有这样一道练习题：4.08dm2=（ ）dm2（ ）cm2这是一种关于复名数与单名数的转化题型。学生由于审题不清，会简单地对原数据进行单位换算，甚至对单名数与复名数之间的转换方法混淆不清，导致出现这样的错误：4.08dm2=（4.08）dm2（408）cm2。如何帮助学生突破这一难点呢？为此，笔者将这道题的错误答案出示给学生，引导学生思考：想一想这道题错在哪里。与此同时，笔者又出示了同类题4.08dm3=（ ）L=（ ）mL，并启发学生比较这两道题目，看看能够从中发现什么。学生认为这两道题相差一个等号，但表示的意思完全不一样。第一道题4.08 dm2=（ ）dm2（ ）cm2，这实际上是把单名数拆分成复名数，也就是把4.08 dm2分成4 dm2与0.08 dm2，第1个括号内填入4，第2个括号内填入8就可以了。而第二道题，4.08 dm3=（ ）L=（ ）mL就复杂了，这是由4.08 dm2=（ ）dm2和4.08 dm2=

（ ）cm2这两道题组成的。

学生分清了这两道同类题目的区别之后，笔者又出示了相应的练习题：5.06 kg=（ ）kg（ ）g

3.6 dm3=（ ）L=（ ）mL

有了这个相似内容的比较之后，学生掌握了单名数与复名数、复名数与复名数之间的转化方法，同时也对单位换算有了深刻的理解，对相近知识能够进行串联，从而实现主动迁移、有效整合。

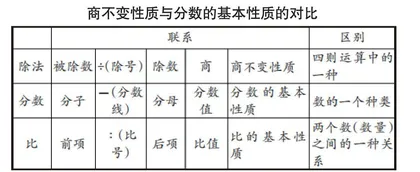
在教学中，让学生比较学过的相似内容，这是帮助学生串联知识点、建立知识体系的有效方法。比如，学生学完了六年级上册“比的基本性质”之后，笔者让学生结合学过的知识“商不变性质” “分数的基本性质”进行比较（见下表）。

商不变性质与分数的基本性质的对比

由此，学生对除法、分数和比之间的相同点和不同点有了深刻的理解，形成了一个完整的知识链条。

二、运用比较策略，区分易混内容

在数学学习过程中，往往会有一些易混淆的数学概念，运用比较策略能帮助学生有效区分概念的本质，加深对数学知识的理解。

比如，有这样一道练习题：飞机模型A在空中飞行6分钟，飞机模型B的飞行时间比飞机模型A的飞行时间短分钟。飞机模型B的飞行时间是多少？学生由于受到解决分数问题思维定式的影响，不自觉地就把分钟看成了分数，导致出现错误的计算结果。为此，笔者先给学生出示错例6×（），引导学生思考：你能发现错在哪里吗？学生指出，是一个数量，因为它带有单位名称，不应该是一个分数，所以答案应该是6-。学生有了认识之后，笔者又出示了以下一组练习题：

①香蕉比桃子多5个，桃子比香蕉少几个？

②香蕉比桃子多，桃子比香蕉少多少？

③甲数比乙数多，乙数比甲数少几分之几？

④甲数比乙数多，那么乙数比甲数少几分之几？

这4道小练习层层递进，学生步步深入，逐步发现了一个规律：如果一个数比另一个数多（A为自然数），那么另一个数就比这个数少;如果一个数比另一个数多（X，A为非0自然数），那么，另一个数就会这个数少。

在上述实践中，学生通过比较，区分了易混淆的分数知识，对分数的单位“1”有了透彻的理解，并且能够熟练运用字母表示数的数学知识，归纳总结得出一个准确的数学规律。在这个过程中，学生不但提升了数学推理能力，而且对所学的分数概念有了深刻的建构。

类似引起学生负性迁移的内容还有很多，比如在解方程时，40%的学生运用的方法是左边乘5，右边也乘5。究其原因在于，学生之前学过分数除法，比如，学生如法炮制，不假思索地解决方程问题，由此产生了负迁移。这时，教师可以给学生出示方程，将其与进行对比，比较这两个方程在解法上的相同点和不同点。通过对比，学生认识到，解方程时，左右两边应同乘除数，而不是乘除数的倒数。由此，学生将分数除法和解方程进行了有效的区分，找到了两者本质的区别。

三、运用比较策略，深化知识提升

学生在学习的过程中，思维大多处在浅层，对知识的理解不深入，这就需要教师运用比较策略，帮助学生深度学习。

比如，学生学完分数之后，在做这样一道练习题时出现了错误：小明小时走了千米。他每小时要走多少千米？走1千米要用多少小时？这道题目学生之所以会出错，是因为学生不能深刻地理解分数所表示的数量关系。为此，笔者出示了一道练习题：小明2小时走10千米，每个小时走多少千米？走1千米要用多少小时？在这道练习题中，学生要弄清楚的是题目中的数量关系。笔者启发学生思考：2小时是指什么？10千米是指什么？问题中要求的分别是什么？这样的分析，能帮助学生梳理清楚速度、时间和路程这三者之间的关系。学生认识到，要求出速度，就要把10千米平均分成两份，求出每一份是多少。通过对这道题目的分析，学生找到了解答的方法，然后把这种数量关系正向迁移运用在分数中。学生通过对两道题目的比较，找出异同点，发现只要把整数变成分数就可以顺利解决这个问题了。

针对知识之间的异同进行相互比较，从而促进学生知识的提升，这是提高课堂学习效率的有效方法。例如，在学习圆柱的体积计算公式时，笔者让学生观察圆柱体转化成近似长方体的模型，让学生思考：转化前后发生了什么变化？学生认为，圆柱转化成长方体后，它们的体积相等，但是表面积增加了两个半径乘高的长方形。在此基础上，笔者带领学生回想之前学过的知识：把圆转化为近似的长方形之后，发生了什么改变？学生认为面积没有变化，周长增加了两条半径。笔者继续引导学生进行比较，看看能得出什么样的结论。学生发现，平面图形，如圆转化时增加了周长，立体图形如圆柱体转化时增加了表面积。通过比较，学生对知识间的理解更加深入，由此获得了思维和能力的发展，深化了学生对知识的应用。

综上所述，在数学课堂教学中，学生会由于各种各样的原因遇到学习难点。这些原因是多方面的，既有教师的原因，也有教材的原因，还有学生本身的原因。运用比较策略，能够帮助学生突破学习难点，解决学习中出现的困惑。这就需要教师从教材入手，深入钻研数学知识，找准学生错误的源头，针对学生容易出现的问题对症下药，有的放矢引导学生展开对比，让学生的数学核心素养获得有效的提升。

【参考文献】

[1]戚宝荣.小学数学分层练习优化设计策略[J].华夏教师，2018（34）.

[2]程明喜.小学数学“深度学习”教学策略研究[J].数学教育学报，2019（4）.

[3]李进存.小学数学教学中的有效引导策略探析[J].西部素质教育， 2016（2）.