依心循理，破立相济

全景教育

研究学生，懂得学生，懂得学生如何学习，是教育中最关键、最重要的事。2017年，我在接受《中国教师报》记者专访时，谈到对全景式数学教育教师团队专业成长的理想时，曾这样殷切地希望：“我和全景式数学教育团队的每一位成员，接下来要苦修儿童心理学、脑科学、认知科学、人学、社会学，真正理解儿童、懂得儿童，理解人，懂得人，从经验之师走向科学之师，从经师真正转变为人师。”本期安排的四篇文章，是全景式数学教育团队的核心成员尝试以“心理动力学、认知心理平衡理论、格式塔学派的整体优先效应（全景式数学理念之‘在整座森林中研究一棵树、大意义整体教学’均源于此）、皮亚杰建构主义理论”为指导，从儿童认知科学和学习心理的视角分析、设计学习活动，分析和实施教学的过程的尝试和探索。目前，我们的认识还是粗浅的，探索还是初步的，权作抛砖引玉，不当之处，敬请各位同仁批评指正。

（张宏伟）

【摘 要】以“认知心理学”为依据，利用“心理动力学”“认知心理平衡理论”，针对“归一应用题”设计了独特的“4破5立”教学，学生的认知在平衡不断被打破与重建的过程中愈加完整、全面，解决问题的策略不断丰富，学生在实现学习目标的同时能够把学习重心更多地聚焦在“完整思维、学会思考、激发创新、开慧启智”上。

【关键词】心理动力学 认知心理平衡理论 归一问题 “4破5立” 策略多样化

传统的“归一应用题”，现今一般编排在三年级，归属于“解决问题”。其主要任务是让学生用学过的知识、技能、方法等解决现实中的实际问题。它是培养学生的应用意识、理解数学和生活、学会分析问题和解决问题的基本方法，是发展学生思维的重要路径和载体。全景式数学教育团队对这节课做了新的尝试：以“认知心理学”为依据，科学利用“心理动力学”“认知心理平衡理论”，设计了独特的“4破5立”教学。在实现上述目标的同时，学生更多地把学习重心聚焦在“完整思维、学会思考、激发创新、开慧启智”上。

“4破5立”中的“破”是指学生突破自己现有的认知平衡状态，“立”是指学生原来已经有的或者重新建立起来的认知平衡状态。

认知平衡理论认为：人总是具有力图保持其内部认知系统平衡与和谐的心理倾向，当新场景中的认知因素与个体原来的认知不同或冲突时，他内部认知系统的平衡与和谐便会被打破，进入不平衡状态。而这种不平衡的认知状态具有较强的动机性，会促使人积极主动改变其认知系统的某些因素，或改变现存的认识，或添加一种新的认识，以达到平衡状态或校正不平衡，最终重新建立新的认知系统平衡……

全景式数学教育下归一问题的学习过程依据上述理论设计，构建了“平衡—打破—……—平衡—打破”如此不断扩展、循环攀升的认知心路历程和思考过程。教学中还利用心理动力学不断激发和强化学生的兴趣与探究欲，文中在相应的实录后进行了分析与说明。

实录和分析

一、1“立”——意料之中：知道……就可以……

1.教师从左向右依次板书如下3个问题，同时，请学生独立静思：“只要知道……就可以求出……”。

（1）一辆汽车， ，7小时行多少千米？

（2）盐外附小三年级， ，6个班有多少人？

（3） ，8支铅笔一共多少钱？

2.学生踊跃反馈，教师根据学生反馈，构成完整题目，并解答。

第（1）题补：每小时行9千米;第（2）题补：每班有32人;第（3）题补：一支铅笔5元钱。

师：请同学们比较一下这3道题，虽然它们说的事不同，数量不同，但是它们有一个共同的特征——只要知道什么，就能求什么。

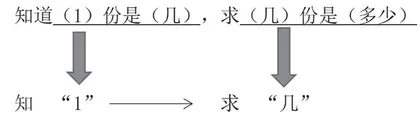
引出：

师：知“1”→求“几”，用乘法。

【学生从一年级就开始学习应用题的基本结构、基本思路和解答流程，低年级形成了分析应用的格式：要求什么，就必须知道谁和谁。到学习归一问题时，学生已经强化了近5个学期。学生建立了相应的稳固的认知平衡，且这种平衡对学生而言已成定式，从所有的学生都使用了“必须”可以看出，学生把求多份量的前提更多单一地定向为“一份量”，对解决问题所需条件的多元化认识产生了负向迁移。第二个教学环节就是对学生这种已有认知平衡的打破。】

二、1“破”——意料之外：还可以……

师（发出挑战）：求8支笔一共多少钱，难道只有知道1支笔的价钱才能求出来吗？（全班一时默然）

过了一会儿，几个学生突然大呼：噢……我知道了！

一个学生情不自禁站起来激动地自说自话：知道2支铅笔……

师：停！我知道你已经想通了，牛！下面的话不说了，给还没有想好的同学留一些独立思考的时间。

【思考的独立是心理独立的重要路径和标志，同时也是创新的核心。教师在教学中一定要给学生提供充分的独立思考的时间和空间，最大化地呵护和激励学生独立思考的积极性、主动性。】

教师又等了一会儿，学生纷纷举手示意自己也想到了，比如，知道2支笔10元钱，也能求出8支笔一共多少钱。（学生解法和反馈略）

师：这道题是属于知道什么是多少，求什么是多少。

生：知道“几”是多少，求“几”是多少。

师：这两个“几”表示的数量一样吗？（生：不一样！）

教师用不同颜色的笔标出两个“几”，以示不同：这道题知道“几”是多少，求“几”是多少。

小结：求“几”是多少，可以寻找的条件有（ ）或者（ ）。

【上面教学环节中，有学生只说出一半的话“知道了2支……”像一重锤，把其他学生保持了5个学期的平衡破开了一个口，产生了“鲶鱼效应”，启发和激发了每一个同伴重新审视自己的认知，探寻另外一种可能。经过自己的思考和群体思维的碰撞，原来狭隘的认识得到矫正，添加了一种新的认识——知道“几”也可以求“几”。至此，寻找解决问题的方向从一个维度变为两个，应用题新的构成要素和框架重新建立平衡，但是，这个刚刚建立起的平衡还是比较弱的、不甚牢固的。】

三、2“立”——求“几”，先求“1”

师：刚才第一步用10÷2=5（元）的目的是什么？

生：把知道“几”是多少，变成已知“1”是多少。

师：这实际上是用转化的思想把“知道‘几’，求‘几’”简化为“知道‘1’，求‘几’”。

总结：知道“几”是多少，求“几”是多少的解答思路是什么？

生：知道“几”是多少，求“几”是多少，先求出“1”是多少，再求“几”是多少。

教师板书箭头和步骤序号，形成如下板书，建立知道“几”求“几”的第一种解决方案。

师：也就是说，要求几份是多少，既可以寻找相对应的1份是多少，也可以寻找几份是多少。

补充板书如下：

【通过这个环节的跟进学习，不仅使刚才建立起的弱平衡（归一问题结构框架）得到强化，还打通了“知1份”和“知几份”间的联系，形成了解决归一问题的基本方案和流程，使认知的新平衡更为丰富、完整和稳定。】

四、2“破”——还可以怎么样想？

教师指着黑板上的题目和解法问：“2支笔10元钱，8支笔多少钱？”难道只能这样做吗？还有别的方法吗？你做做我看看。

学生独立思考，自行尝试各种办法。（教师巡视，不断激励和引导学生，并收集学生的作品。）

展示学生作品：

8÷2=4 10×4=40（元）

8÷2=4（个） 10×4=40（元）

8÷2=4（支） 10×4=40（元）

8÷2=4（份） 10×4=40（元）

师：最后的结果都等于40元。这种做法极可能是对的。现在最重要的是，我们必须理解透它的每一步表达的意义。第一步“8÷2”是想先求什么？得数4后的单位到底是支，是个，是份，还是什么都不是？（大多数学生都非常茫然）

【第1次打破的是解决问题的前提和结构，这次打破的是解答归一问题的策略和方法。】

五、3“立”——先求“倍”，再求“几”

师：大部分同学都不会。画图可以帮助我们分析和理解。我们一起画：用1根竖线代表1支铅笔，2根竖线就代表2支笔。为了便于对比，我们在第二行对应着画出要求的8支铅笔，这样便于对比和分析……

最后形成的板书如下：

【其实，这个学生此时处于认知的“次平衡”状态。她通过观察绝大多数同学和教师的反应知道这种解法是对的，但是自己又想不明白，经过短暂的挣扎与矛盾之后，不排斥但也不接受，处于一种中立状态，即认知的次平衡状态。】

教师指着学生一开始的反馈问：把已知的2支看成一盒，8支就相当于4盒;把2支看成……

学生：把2支看成1份，8支就是4份……

教师把原来的板书改为：

8÷2=4倍   8÷2=4（对）   8÷2=4（组）   8÷2=4（份）

（这里的倍不需写，简写为8÷2=4）

师：知道“几”是多少，求“几”是多少的第二种解法是什么？

生：先求要求的那个“几”是知道的那个“几”的倍数，然后再求“几”是多少。

教师板书：

小结：知道“几”是多少，求“几”是多少。到目前为止，同学们思考出了两种解决路径：路径A是先求“1”是多少，再求“几”是多少;路径B是先求倍数，再求“几”是多少。

【“倍比”与“归一”是显著不同的两种思考，对三年级学生而言是很有挑战性的（教材上没有编排），而一切富于挑战性的事物或活动都有着深刻的心理动力学意义。课堂上学生积极投入的热情状态，以及解决问题后的兴奋都表明：学生是非常享受这种挑战带来的刺激的。】

六、3“破”——“倍”感不适

教师随手在黑板上写出一道题：24支笔120元，8支笔多少钱？

第一步，学生判断出这道题属于知道“几”是多少，求“几”是多少。

师：这样的题，你有几种解决路径？试一试。（学生独立尝试练习）

学生作品1：120÷24=5（元） 5×8=40（元）。（教师让学生说自己的思路）

学生作品2：24÷8=3，3×（学生抓着头叙述完自己的思路：我先算24支笔是8支笔的几倍，求出来是3倍。再算8支笔的钱，我想用3×120，可是我一口算得360元，8支笔不可能是360元呀，我也不知道怎么回事，就没往下写。）

教师引导其他学生一起思考该学生的问题，找出问题到底出在哪里。

【学生刚刚建立的“先求倍数，再乘”的认知再次失衡，让学生“倍”感不适，又欲罢不能，再次平衡的渴望促使他们更为积极地思考和探索“问题到底出现在哪里”。】

七、4“立”——全景倍的关系和运算

学生作品3：24÷8=3，120÷3=40（元）。

师：她这个结果是40，奇怪，我们原来做的这些题算出了倍数后，不都是乘吗，她怎么除了呢？你自己琢磨琢磨，小组间也可以商量商量。

最后，所有学生都明白了，并做了如下讲解：

这道题知道的这个“几”是多的，求的那个“几”是少的。这里的3倍，表示知道的这个钱是3份，求的钱才是1份。知道3份是120，求1份，用除法，不用乘法。（听课教师自发鼓掌）

教师让几个小组把这个思路阐释几遍后，问：那先求倍数，再求“几”的这种思路，什么时候用乘，什么时候用除，你们能总结一下其中的规律吗？

生：把知道的那个“几”和要求的那个“几”比，如果知道的“几”少，用乘法，如果知道的“几”更多，用除法。

【此时，归一应用题的“倍比”解法再次得到矫正、补充，倍比解法重新获得平衡。】