巧建模 悟本质

《图形的运动（三）》的教学重点是围绕旋转方向、旋转角度、旋转中心建构旋转运动的认知模型。如何引导学生迁移已有的对图形平移运动特征的认知，以及建构这种认知的学习路径，通过直观操作，感悟旋转运动的本质，建构旋转运动模型，提升数学素养呢？

一、找准认知起点，让探究方向更明确

《图形的运动（三）》——旋转是人教版数学五年级下册的教学内容。在第二学段，学生通过对轴对称图形和平移运动的探究，已经积累了探究图形运动的基本方法和经验，知道描述平移运动必须具备两个要素：一是找准平移方向，二是找准在此方向上平移的距离。这是学生描述图形运动的知识与经验起点。教师找准学生的认知起点，能让探究方向更明确。

如何清楚地描述图形的旋转运动过程呢？课堂上，笔者先出示教材第83页例1（指针旋转图），让学生说说指针在做什么运动。学生回答“旋转运动”后，笔者引导学生回顾研究图形运动的要素。学生回答：我们在四年级学习了图形的平移运动，是从平移的方向和距离展开探究的，所以研究旋转运动可能也要从这两个方面着手。明确探究方向后，笔者重点引导学生横向迁移知识，寻找解决新知的基本学习方法。笔者提问：观察例1，指针从“12”走到“1”，你能把这个指针的旋转过程用数学语言完整地描述出来吗？一名学生回答：指针向右运动。另一名学生纠正道：指针是沿弧线运动的，运动方向随着指针旋转依次指向“1、3、6、9”等，指针的朝向不断变化，所以向左、向右、向上、向下等用于描述平移运动的词，不适用于描述旋转运动。其他学生纷纷点头赞同，笔者乘机引导：如果不能用“向右”描述指针旋转的方向，那该怎样描述呢？一名学生提出可以用“顺时针方向”来描述。由此，笔者引出了顺时针方向和逆时针方向。从平移运动的方向到旋转运动的方向，学生经历了思维的跃迁，找到了描述新的图形运动的方法。

二、抓准问题冲突点，让概念理解更通透

准确把握认知冲突是探究活动有效开展、有序推进的动力源，是学生通透理解数学概念的关键点。学生在上一个环节通过知识的正向迁移，准确描述了图形旋转的方向。本环节，笔者要重点解决的问题是如何准确描述旋转的距离。

笔者引导：指针从“12”走到“1”，如何描述旋转的距离呢？学生回答：指针从“12”走到“1”，顺时针走了1格。笔者借助课件，对比演示旋转中的1格（一段弧线）与平移中的1格（一段线段），并引导：你还坚持用1格描述旋转的距离吗？学生观察后发现，不能用几格表示旋转的距离，因为弧线无法用“几大格”“几小格”“零点几格”表述，并提议把弧线拉直后量取其长度，用长度表示旋转距离。笔者肯定了化曲为直的想法，但也说明了实践中不好操作，让学生再想想其他办法。学生小组讨论后提出：弧线上的距离可以用角度描述，旋转一周是360°，把360°平均分成12大格，每大格是30°，这样指针从“12”走到“1”就可以描述成“顺时针旋转30°”。本环节，笔者没有急于揭示答案，而是通过适时、适度的引导，引导学生借助几何直观抽象出用角度描述旋转距离的方法。

随后，笔者让学生再次描述指针从“12”走到“1”的运动过程。学生回答：指针从“12”走到“1”，按顺时针方向旋转了30°。为引导学生关注旋转中心，笔者制造认知冲突，用课件动态演示指针绕3个不同的旋转中心（绕指针的一个端点旋转；绕指针的另一个端点旋转；绕指针的中点旋转）顺时针旋转30°后的样子，并质疑：指针按照同学们的要求旋转了，旋转的结果怎么不一样呢？学生马上发现用方向和距离两个要素无法准确描述旋转运动，还要关注绕哪个点旋转。由此，笔者引出“旋转中心”的概念。这样教学，学生深刻理解了描述图形的运动，旋转方向、旋转角度、旋转中心缺一不可。

三、确准认知难点，让模型构建更全面

为了让学生全面建构图形旋转运动的模型，准确、熟练地描述图形的旋转，笔者把教材中的习题进行变式，引导学生通过变式练习深化思维层次，感悟旋转三要素之间的关系。

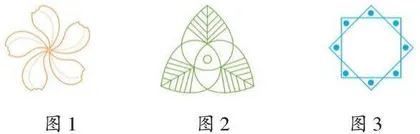
课堂上，笔者出示下图，让学生先找出基本图形，再指出旋转中心，最后说明旋转角度。

以第三幅图为例，学生观察后提出：这幅图的基本图形是正方形，也可以是小三角形；如果以正方形为旋转的基本图形，旋转中心在正方形内部，即正方形两条对角线的交点；如果以小三角形为旋转的基本图形，旋转中心在三角形外部，也是正方形两条对角线的交点。由此，学生发现图形旋转的基本图形不唯一，旋转中心不仅可以在图形的顶端（如图1），也可以在图形的内部（如图2），还可以在图形的外部（如图3）。变式训练培养了学生的观察能力和发散思维，使他们在知道旋转角度不同，形成的旋转图案不同的基础上，进一步认识到旋转中心的位置不同，得到的图案也不同，从而更深入地理解了图形的旋转模型。

（作者单位：谢志勇，武汉市新洲区教学研究室；曹铮铮，武汉市新洲区第一初级中学）

责任编辑 刘佳