初中数学竞赛中图形旋转变换问题探微

作者简介：李军（1988～），男，汉族，安徽无为人，江苏省南京市南京师范大学附属中学树人学校，研究方向：竞赛数学、中高考志愿填报机制。

摘 要：图形旋转变换问题是初中数学竞赛中的一种常见题型。对学生而言，此类题型也是数学竞赛中的一个难点。观察能力欠佳、生活经验不足、解题思路较窄是导致图形旋转变换问题教学效益低的重要因素。鉴于此，教师应采取创设情景、联系生活、变式训练等策略，循序渐进、有的放矢地提升图形旋转变换问题的教学效益，促进学生逻辑推理、数学抽象、直观想象等核心素养的全面发展。

关键词：初中数学竞赛；图形旋转变换；问题探微

中图分类号：G633.6 文献标识码：A 文章编号：1673-8918（2023）47-0064-04

以赛促学是发展学生数学核心素养、提升数学教学效益的一条有效途径。数学竞赛能够较为全面、客观、准确地检测学生的数学核心素养，能够挖掘学生的数学潜能，调动学生学习数学的积极性。图形旋转变换是初中数学竞赛中的一种常见题型，也是一个教学难点。鉴于此，教师应通过细致了解图形旋转变换问题的教学意义，透彻分析图形旋转变换问题的教学困境，深入探究图形旋转变换问题的教学策略，着力提升图形旋转变换问题的教学效益。

一、图形旋转变换问题教学意义分析

逻辑推理能力、直观想象能力和数学抽象能力等，都是初中数学教学中发展学生核心素养的基本内容。“图形的旋转”是苏科版八年级数学下册中的内容。在解决图形旋转变换问题时，学生需要进行逻辑推理、直观想象以及数学抽象等，因此，图形旋转变换问题有助于培养学生的逻辑推理能力、直观想象能力和数学抽象能力等。

（一）有助于培养学生的逻辑推理能力

逻辑推理是指根据已有事实，或已知命题，遵循逻辑规则推理出一个新命题的思维过程。在解决图形旋转变换问题时，学生需要根据已知条件（已有事实），以及与图形旋转变换相关的已知命题，层层深入推导、推理出未知条件。在此过程中，学生的逻辑推理能力也会逐步发展。

旋转的概念、旋转三要素（旋转中心、旋转方向和旋转角）、旋转形成的条件（一个中心、一个方向和一个角度）、旋转的性质等，都属于已有事实，都是学生解决图形旋转变换问题的主要依据。为了能够有序、有效解决与图形旋转变换相关的数学问题，学生必须要深度理解、熟练掌握、灵活运用这些数学知识。在解决不同类型的图形旋转变换问题时，学生需要运用关于图形旋转的不同概念。如：当学生在判断“国旗上升、足球滚动、风车旋转”等生活现象是否属于旋转时，需要根据旋转的概念、旋转的三要素这些已知事实、已知命题，进行逻辑推理。

以解决图形旋转变换问题为契机，学生不仅能够更进一步地理解与图形旋转变换相关的数学概念，而且能够循序渐进地发展自身的逻辑推理能力。随着学生逻辑推理能力的提升，他们解决各种数学问题的能力也会得到提升。

（二）有助于培养学生的直观想象能力

直观想象是指借助于几何直观和空间想象能力，感知事物形态、物象变化的一个过程，也是学生以图形为支架，分析、解决问题的一个过程。通过启迪、指导学生有效解决图形旋转变换问题，能够促进学生直观想象能力的发展，进而提升学生解决数学问题的能力。

例如，在引领学生解决图形旋转变换问题时，为了降低学生解决问题的难度，提升学生解决问题的效度，教师需要利用信息技术手段，联系实际生活，创设形象生动的教学情境；教师也需要利用一些实物教具，让学生直观感知、细致探究图形变换规律等。无论是教师利用信息技术手段创设的教学情境，还是教师利用实物教具创建的学习场域，都能够将抽象、复杂、枯燥、低效的图形旋转变换问题形象化、简单化、趣味化、高效化。尤为重要的是，通过探究、分析、解决图形旋转变换问题，学生的直观想象能力能够得到发展与提升。

在教师的指导下，学生通过依托教学情境、借助实物教具有效解决图形旋转变换问题，能够更为清晰、准确、真切地感知图形旋转变换规律，能够逐步形成直观想象能力，进而促进学生数学核心素养全面发展。

（三）有助于培养学生的数学抽象能力

从数量与数量关系、图形与图形关系之中，抽丝剥茧抽象、概括、总结出数学概念的过程，是发展学生数学抽象能力的一个过程。图形旋转变换问题重在研究图形旋转之前与旋转之后、图形旋转与图形静止之间的关系。因此，图形旋转变换问题有助于培养学生的数学抽象能力。

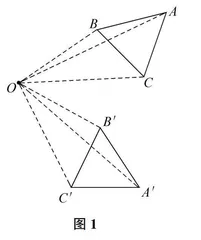
例如，在引领学生探究图形旋转的概念时，教师借助板书（如图1）向学生展示了△ABC旋转的过程。通过观察教师的板演，学生发现：△ABC在旋转过程中，始终围绕O点；在旋转一定的角度之后，△ABC到达了一个新的位置，且从原来的视角观察时，该三角形的形态也发生了一些变化，即△A′B′C′，但实际上，△ABC的形状与大小并没有发生改变，只是改变了图形在平面中的位置。根据△ABC在平面中旋转的全过程，学生能够抽象、概括出图形旋转的概念。

从上面的案例可以看出，通过思考、分析、解决图形旋转变换问题，学生不仅能够形象直观地观察图形旋转变换的过程，而且能够概括、提炼出图形旋转的抽象概念。而这，也有助于促进学生数学抽象思维能力的发展。

二、图形旋转变换问题教学困境分析

找准图形旋转变换问题教学的现实困境，是实施图形旋转变换问题教学的切入点。从多年辅导学生参加数学竞赛的经历来看，图形旋转变换问题教学所面临的困境主要包括以下三个方面。

（一）观察能力欠佳

细致、准确地进行观察是学生解决图形旋转变换问题的基本方法。但是，因为学生观察能力欠佳，所以无法细致入微、准确无误地观察图形旋转变换的过程，导致他们找不到解决问题的切入点，进而影响解决问题的效果。观察的角度、方法等，是影响观察能力的关键因素。

例如，一个三角形经过多次旋转之后，形成了一个新的图形（如图2），问：这个图形是该三角形旋转多少次而形成的？每次都旋转了多少度？在解决这两个图形旋转变换问题时，学生需要仔细观察图2，然而，因为学生的观察能力参差不齐，所以他们的观察结果也千差万别。学生甲说：新图形是原三角形旋转10次形成的，每次旋转了36度。学生乙说：新图形是原三角形旋转8次形成的，每次旋转了45度。学生丙说：新图形是原三角形旋转7次形成的，每次旋转了45度……显然，学生甲和学生乙的答案都是错误的，只有学生丙的答案是正确的。通过与学生进一步沟通，教师发现：学生甲和学生乙之所以会出现错误，主要是因为他们的观察方法欠妥，观察能力欠佳。

学生的观察能力并不是与生俱来的，而是经过后天培养逐步形成的。既然学生观察能力欠佳，那么，教师就应该立足图形旋转变换问题，有的放矢地培养学生的观察能力。

（二）生活经验不足

数学与生活之间有着密不可分的联系。各种图形旋转变换题目源于多姿多彩的现实生活场景。但是，因为学生的生活经验不足，即在现实生活中未曾经历、体验过相关的生活场景，所以他们对图形旋转变换题目理解不透彻、不准确。此外，生活经验的不足，也会导致学生无法将图形旋转变换与现实生活联系起来。

例如，有一块直立在地面上的长方形空心砖ABCD（如图3），工人师傅将这块砖轻轻地推倒。在此过程中，空心砖的A点始终保持不变，B、C、D点发生了旋转，分别旋转到了B′、C′和D′，构成了一个新的长方形AB′C′D′，问：该空心砖旋转过程中的旋转中心在哪？该空心砖旋转了多大角度？因为学生在实际生活中未曾有过在地面上旋转空心砖的经历，所以他们对该生活场景比较陌生。相关生活经验的缺乏，也成为学生解答这道题目的主要障碍。

在解答图形旋转变换题目时，如果学生生活经验不足，那么，他们就无法基于已有生活经验解决相关问题。因此，根据图形旋转变换的过程，联系实际生活，创设相关的情景，也就成为教师丰富学生生活经验的有效路径。

（三）解题思路较窄

同样的问题，往往可以从不同的角度予以解决。此举能够拓展学生的解题思路、提升学生的解题能力。聚焦学生解决图形旋转变换问题的过程，可以发现：解题思路较窄是图形旋转变换问题教学所面临的现实困境之一。窄化的解题思路，禁锢了学生的解题思维，降低了学生的解题效果。

例如，在解答一些图形旋转变换问题时，因为学生循规蹈矩、思维僵化，所以解题步骤烦琐、解题过程复杂、解题错误频出。同时，学生创新思维的发展也会受阻。学生之所以循规蹈矩、思维僵化，一方面，是因为教师在指导学生解答图形旋转变换题目时，未能有序、有趣、有效地开展变式训练，未能有针对性地拓展学生的思维和解题思路；另一方面，是因为学生缺乏创造性解决问题的意识、能力，教师未能通过启迪、点拨、评价唤醒学生的创新意识、点燃学生的创新激情等。

窄化的解题思路不仅会影响学生的解题效果，而且会影响学生创新思维的发展。因此，在图形旋转变换教学中，适时适当地拓展学生的解题思路，也就成为教师提升教学效益的当务之急。

三、图形旋转变换问题教学对策分析

针对图形旋转变换问题教学中所面临的学生观察能力欠佳、生活经验不足以及解题思路较窄等现实困境，教师应采取创设情景、联系生活和变式训练等策略，培养学生的观察能力、丰富学生的生活经验以及拓展学生的解题思路，以此提升图形旋转变换问题教学的效益，促进学生直观想象、数学抽象和逻辑推理等核心素养的全面发展。

（一）创设情景，培养学生的观察能力

鉴于学生观察能力欠佳的现实问题，教师可依托信息技术、利用实物学具，创设图形旋转变换情景，以此拓展学生的观察视角，指导学生熟练掌握各种观察方法，提升他们的观察能力。

1. 依托信息技术，创设图形旋转变换情景

随着教育信息化时代的到来，信息技术在初中数学教学中的运用越来越广泛。为了让学生动态观察、深入探究图形旋转变换的过程、规律等，教师可依托信息技术手段，创设图形旋转变换情景。

例如，某学生将一张长方形的白纸ABCD（如图4）沿GH对折之后，点C落在了点Q处，点D落在了点E处，EQ与BC交于点F，若AD=8cm，AB=6cm，AE=4cm，则△EBF的周长是多少厘米？因为学生受到自身空间想象能力的限制，所以他们无法想象、观察题目中所描述的问题情景。为此，教师依托信息技术手段，动态展示了该问题情景。与此同时，为了引领学生更为细致地观察图形旋转变换过程，教师还利用信息技术手段，多视角、全方位地进行了展示。

信息技术的巧妙运用，让学生观察长方形白纸ABCD沿GH对折过程的视角更广阔、更细致，原本抽象、复杂的问题情景变得形象、简单。依托信息技术创设教学情景，能够降低学生解题的难度，提升学生解题的效度。

2. 利用实物学具，创设图形旋转变换情景

为了让学生理解抽象的图形旋转变换过程，教师也可以组织学生利用一些实物学具，自主创设图形旋转变换情景。如此，在动手操作、亲身体验的过程中，图形旋转变换情景就会变得可视、可触。

仍然以“某学生将一张长方形的白纸ABCD沿GH对折”的问题情景为例，教师可指导学生拿出一张白纸，并根据题目要求动手折叠。在此过程中，一张貌似微不足道的白纸，就成为学生的实物学具。聚焦真实、有趣的折纸活动，学生能够直观、清晰地观察、了解题目中长方形白纸的旋转变换过程。而这，也有助于学生找准解决问题的切入点，提升学生解决问题的实效性。

此外，在实际教学中，教师可组织学生根据图形旋转变换的问题情景，利用废旧纸盒、雪糕棒、棉签棒等低成本物品，制作一些简易学具。之后，指导学生利用这些实物学具，模拟演示问题情景中图形旋转变换的过程，将抽象的问题形象化、复杂的问题简单化。