数形结合解题思路在初中数学教学中的应用方法探究

摘 要：代数与图形是初中数学学习中的两大要素和主要研究对象，初中数学教学内容处处涵盖数形结合，它既是一种题目类型，也是一种思维方式与解题思路，学生要想更好地掌握初中数学教学内容，就必须掌握好数形结合的解题思路。教师在对初中生展开数学教学时，必须将数形结合渗透到课堂教学中，为学生打下一个良好的思维基础，为高中数学大量的数形结合问题的解决做准备。文章对数形结合在初中数学教学中的运用方式进行探究。

关键词：数形结合;思维方式;数学教学;运用能力

中图分类号：G633.6   文献标识码：A   文章编号：1673-8918（2022）06-0070-04

一、 引言

初中数学中涉及大量的几何问题与代数问题，几何与代数的联合在初中数学中也十分常见，很多时候数与形是分不开的，有学者认为数与形之间的关系类似与钥匙与锁之间的关系，数与形双方都可以是钥匙也可以是锁。当我们将数与形互为工具，最终的目标在于解决问题，当“形”为已知量，那么数就是钥匙，当“数”为已知量，那么“形”就是钥匙。通常来讲“形”更加的直观，教师在展开数学教学时，可以将“形”作为一种教学工具，将抽象的知识图形化、具体化，从而帮助学生更好地理解，培养学生的抽象思维。

二、 数形结合的四种形式

（一）以形变数

以形变数适用于几何知识教学，这时候“形”，也就是几何图案为已知，教师通过赋予不同几何图形、同一几何图形不同组成部分数字的概念，帮助学生借助数字建立不同几何图形之间、同一几何图形不同组成部分之间的联系，帮助学生对几何图形内涵进行深入了解，从而帮助学生打下几何基础。

（二）以数变形

以数变形适用于数字知识的教学，教师用不同的图形去对数进行解释，从而更好地帮助学生了解数的内涵。比如教师在对七年级上册第一课《正数与负数》一课展开教学时，可以通过画坐标轴的方式将正数与负数在坐标轴上表示出来，教师画出坐标轴以后，分别将-3、-2、-1、0、1、2、3这几个数字在坐标轴上标出来，让学生对不同数字之间的位置进行观察。这样一来，学生可以一目了然地看出负数与正数之间的相对关系，借助图形表示，学生不用对“负数数字越大值越小，正数数字越大值越大”的大小规律进行死记硬背，可以自己从图中得出答案，这样学生记起来也更牢固，不会因为缺乏理解忘记知识。从上述小案例中我们可以发现以数变形教学方法运用的优势。

（三）数形结合与互变

随着初中数学教学难度的不断增加，数字与图形之间的联系也会越来越紧密，因此会涉及数与形的互变。数形互变常见于几何与数字结合习题的解答中，在遇到这种复杂题型时，教师需要引导学生将所有已知量转变为另一种形式，丰富已知量，让解题思路更明朗。

（四）具有几何意义的等式或代数式的结构

数学这一学科题目变化多样，出卷人不仅考查书本上的数学知识，还重视学生数学思维的考查，除了数形结合互换、以形代数、以数代形外，还会出现给出图形，让求数学公式的题目。以2010年浙江湖州的一题目为例，题目中给出甲乙两个图形，两个图形均分为黑白两个部分，并用a、b两个未知量来标出图形边长。题目让根据阴影部位与空白部位的未知量表达以及甲乙两个图形之间的关系来求表示图形面积的数学公式。该题目为非典型以形代数或以数代形题目，与常见函数、图形等知识不相关，而是旨在通过让学生找对应关系的方式来考查学生的数学思维，学生只有具备数形结合的思维，才能找到对应关系，得出答案。

三、 数形结合解题思路总结

从以数助形的解题角度来看，主要包括两种解题思路：一个是利用数轴、坐标系将几个问题转变成常见的代数问题，另一个是用面积、距离、角度等几何量来将几何问题解决，常见的包括用勾股定理对角的类型进行证明、用数字概念的线段来对几何图形的相似进行证明等。根据教学经验，可以发现在用坐标与相关函数公式等解决几何问题的时候，有时候需要借助辅助线来进行解题，这就要求学生具备一定的空间想象能力，能够一眼望去看出给出几何问题的特殊性，并借助这一特殊性作好辅助线，以便迅速将问题解决，借助辅助线解决问题也是初中数学学生学习与教师教学的难点。勾股定理是初中数学教学中重点中的重点，常见用勾股定理证明垂直关系的数形结合题目，该类型题目多用以数助形的方式来进行解答，娴熟的代数运算可有效帮助学生迅速获得解题思路，学生具有较强代数能力之后，对数字与图形结合的敏感度也会随之提升。为提升学生数形结合解题能力，可从提高学生代数运算能力着手。几何图形也可以用来解决代数问题。通过几何图形推导代数公式可以有效避免学生对代数公式死记硬背，从而避免学生在考场上因为对公式不熟练一时间解不出题目。以完全平方公式为例，就可以借助正方形的分割图来帮助学生推导以及解析公式，让学生在理解的基础上将公式记得更牢。再比如梯形面积公式可以通过拼接两个全等梯形为平行四边形的方式来进行推导。数轴以及坐标系可以赋予代数表达式几何意义，能够有效简化或者是解决问题。以绝对值意义的表达为例，绝对值作为数字元素可以用数轴来进行表示，数轴上两点之间的距离就是绝对值。数的大小同样可以用数轴表示，左边的数总要比右边的数小。相反数则可以看作数轴原点两端对称点所代表的数字。函数性质可以以函数图像的方式表现出来，像是函数的倾斜程度、二次函数的开口等都可以从图像上看出来，而一元二次方程的根则刚好可以看作函数图像与坐标轴之间的交点。此外，初中数学教学中学生较难理解的常数项的意义也同样可以用函数来表示，常数项可以看作函数图像与坐标轴的交点。对锐角三角函数来说，可以用直角三角形中的线段比例进行表示。

四、 当前数形结合在初中数学教学中的应用不足

（一）教师忽视对数形结合教学方法的应用

数形结合不仅是一种题目呈现方式，还可以作为一种教学方式帮助学生对数学原理进行理解。不过在实际初中数学教学中，很多教师缺乏这种将数形结合当作教学方法去运用的意识，在一定程度上影响学生接触数形结合次数，影响学生数形结合思维的养成。为此教师在教学过程中要深化对数形结合的理解，发挥逆反思维在教学中的应用作用，从出题人对学生能力考查的角度展开数学教学。

（二）对数形结合的应用不够深入

很多初中数学教师虽然已经将数形结合当作一种教学方法应用到日常的数学教学中，不过由于平时缺少深入探究，数形结合教学方式应用浅，在一定程度上影响教学效果。这和教师对数与形之间的关系研究不够深入有关，要想进一步提升数形结合应用能力，教师就必须加强对数与形关系的理解，多多尝试数形结合的不同教学方法。

五、 数形结合在初中数学教学中的应用方法

（一）借助数形结合原理帮助学生深化知识点理解

很多教师在开展数学教学时，更习惯于将数学学习归结于简单的公式套定，习惯于为学生构建一个数学模型，然后让学生在遇到问题以后将问题已知量与未知量套在这个数学模型上。有些理解能力比较强的学生能对公式的由来以及问题的解决流程进行自我理解;而一些理解能力比较差的学生，在利用公式解决问题的时候往往心中存有疑惑，即便能够根据数学模型指导明确解题流程得出正确答案，从本质上来看，并没有真正对知识进行掌握，这就导致学生在面对更复杂一些的问题时不能够举一反三，也很难将所有知识融会贯通。比如教师在对一元一次方程展开教学时，会将书本上给出的情境案例作为一种数学模型，“已知长方形的面积为5850平方米，长方形长宽之差为25，求长方形的长和宽各是多少”，教师将问题用一个等式来进行描述“x（25+x）=5850”，之后教师直接告知这个等式是一元一次方程，从而让学生对什么是一元一次方程有所了解。这时候虽然对一元一次方程的概念有所了解，但是一旦脱离具体的例题，相信很多学生仍然无法解释到底什么是一元一次方程。

教师在一开始的时候借助图形来帮助学生了解什么是一元一次方程能够帮助学生更好地理解一元一次方程概念。教师可以设置两个简单的等式，分别为y=5x-3和y=x+2，之后教师结合这两个简单的等式设置一个简单的情境，该情境能用5x-3=x+2描述出来即可。然后教师在板书上画一个坐标系，分别在坐标系上将上述两个简单的等式描述出来，两个等式最终会以两条线的形式呈现在坐标系上，而两条线中间交叉的位置就是x的值。从数字与图像的双重角度对等式进行描述，从而帮助学生将等式与图像建立联系，同时丰富学生的解题思路，从而达到更好的教学效果。

（二）利用图形描述将抽象的数学问题具体化

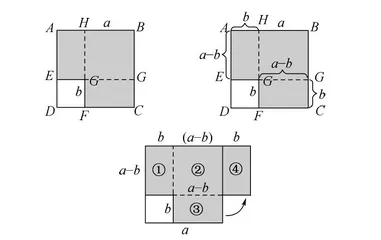
教师在对学生就一些几何知识与几何现象展开教学时，可以借助数字来让几何关系更加直观。比如教师在对等腰三角形的相关内容展开教学时，教师可以不直接告知学生等边三角形的特性，即等边三角形边长相等、内角相等且都为60°，教师可以让学生在草稿纸上画出等边三角形并对边长与角度展开测量。再比如教师在对平方差公式一课展开教学时，要避免直接将平方差公式的用途与计算方式告知给学生，而应借助图形来带领学生对平方差公式进行推导。首先教师在黑板上画一个大四边形，并在四边形的四个角以顺时针分别标上A、B、C、D，之后在AD之间取一点E，在DC边上取一点F，并在大四边形内部取一点G，让EG与GF垂直，EG与DF平行，这样我们就得出了一个大四边形和一个小四边形，小四边形在大四边形内部。将小四边形以外、大四边形以内的面积涂黑，画FG的延长线与AB相交于点H，再画EG的延长线与BC相交于点J，大四边形的边长用a来表示，小四边形的边长用b来表示，带领学生求阴影部分的面积。阴影部分的面积可以用两种方式来表示，两种方式分别得出一个式子，方法一为用大四边形面积-小四边形面积，用式子描述为a2-b2，方法二为用四边形AEGH面积+四边形HBJG面积+四边形GFCJ面积，分别用a与b将上述三个小正方形的面积表示出来。之后引导学生发现GFCJ的面积等于AEGH的面积，然后在黑板上将四边形GFCJ进行旋转从而得到一个新的图形，这时候阴影部分的面积可以用（a+b）[b+（a-b）]来表示，整理之后为（a+b）×（a-b）=a2-b2，最后得出来的就是平方差公式。整个公式推导思路十分清晰，学生只要认真听都可以听懂，起到了将复杂问题简单化的作用，在最大程度上帮助学生进行理解，从而达到更好的教学效果。（见下图）

（三）借助多媒体优化数形结合教学质量，提高课堂效率

传统初中数学教学中，教师在展开数形结合教学时往往是在黑板上现场画图，这在一定程度上影响课堂效率，每节课只有45分钟，教师画一个图至少用5分钟，课堂效率比较低。多媒体教学方式的流行为数形结合教学效率的提升创造了条件，不过很多教师对多媒体的运用能力不够强，在一定程度上造成教学资源的浪费，因此教师应该加强多媒体教学技术探究，提前将课上所需要用到的图形在PPT上呈现出来，将课上画图时间放在课下，从而提高课堂效率。比如教师在对反比例函数展开教学时，反比例函数的内涵比较难理解，教师需要在课前对反比例函数进行深入分析，并将反比例函数与实际生活联系起来，从而帮助学生更好地对反比例函数内涵进行理解，避免陷入盲目套公式的误区。函数的本质在于变量变化规律以及变量之间的关系，教师可以将实际生活联系起来建立函数模型，借助图形与生活实际进一步帮助学生进行理解。生活中能用反比例函数来表示的关系主要有四种，第一个是压力一定时压强和受力面积之间的关系，第二个是电压一定时电流与电阻之间的关系，第三个是长方体容器中水的体积一定时排水量和所需排水时间之间的关系，第四个是气体的气压和气体体积之间的关系。压强、电阻、水压、气压的特性学生在物理课上有所了解，因此在借助这些案例对学生展开反比例函数教学的时候，学生能够较快将反比例函数与原有知识建立联系，更快的理解反比例函数内涵。教师在备课的时候将上述生活实际案例不同变量之间的关系均在PPT上以图像的方式呈现出来，课上先让学生回忆压力与压强以及压力和受力面积之间的关系、电流电压关系、排水体积时间关系，之后再向学生展示提前准备好的图像PPT，引导学生对图像展开观察分析，等学生对反比例函数有了一定概念之后，将提前准备好的例题呈现给学生展开习题训练，对学过的知识进行巩固。