实施“呈题五化”法，培养初中学生数学求异思维能力

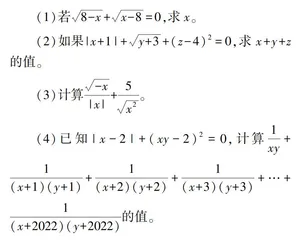
作者简介：蒋萍（1984～），女，汉族，浙江杭州人，杭州市富阳区大源中学，中学一级教师，研究方向：初中数学教学。

摘 要：基于人的个体差异，数学学习对每个学生来说的难易程度是相对的，而每个学生提升学习成绩可是绝对的;面对当前初中学生数学“两极分化”愈演愈烈的情况，文章认为：要实现素质教育、提高初中学生的数学成绩，在课堂教学中，教师不仅要“治标”更应“治本”。让学生感觉学习是一件愉快的、而且是可以实现的事情的前提下，教师通过“呈题五化”法，在解题过程中培养学生的求异思维能力，借此减少初中学生的“学习负担”和“两极分化”现象。

关键词：初中数学;学习负担;两极分化;呈题五化;求异思维

中图分类号：G633.6 文献标识码：A 文章编号：1673-8918（2022）38-0095-04

在大力提倡素质教育的今天，减少义务教育阶段学生的“校内作业”和“校外补课”负担、减少“两极分化”、要求学生全面发展，已成为全社会共识。然而人是具有个性差异的，同样的学习内容和学习要求对不同的人的负担是完全不一样的。所以说，面对当前存在的初中学生数学的“学习负担”越来越重而班级成绩“两极分化”愈演愈烈的情况，不仅要治标更要治本。

研究表明，求异思维具有流畅性、多端性、灵活性、精细性、新颖性等特点;学生求异思维能力的高低，不仅对数学问题的解决有着直接的影响，更是对减轻学生的“学习负担”、减少“两极分化”有着举足轻重的作用。在数学学习的过程中，学习者与众不同的探求思路，别具一格的思考方法，灵活多变的解题技巧，就是学习者求异思维的发展，就是内驱力涌发的标志，就是体现创新素质的萌芽，就是撇开学习负担的基础。教师可通过培养学生具有举一反三的数学求异思维的能力，使学生感觉做数学题目是轻松的，学习数学是快乐的。

要达到上述目的，数学题目的教学呈现尤其重要。笔者在初中数学课堂教学中，借助“呈题五化”法培养学生的数学求异思维，从而减轻学生“学习负担”、减少班级“两极分化”。

一、题目设置梯度化，诱导求异，拓展流畅思维，减轻淤堵压力

学生的求异思维是以其创造性思维作基础的，而创造性思维是强调个体差异的智力品质。由于各人的创造能力不同，所以对同一个数学问题所表现的创造性精神也不同。题目设置梯度化，一题多变，步步推进，可大大增强学生对解决问题思维的流畅性。梯度化题型所催生的思维惯导作用能减轻学生的解题压力，使各层次的学生在问题解决的遨游过程中均有收获。

【例1】 已知在△ABC中，AB=AC，∠A=α，求∠B的度数（应用三角形内角和性质）。

变形1：已知△ABC中，AB=AC，∠EAC是∠BAC的补角。∠EAC=α，求底角∠B的度数（应用等腰三角形性质和三角形外角性质）。

变形2：在等腰△ABC中，若∠A=40°，则∠B=___________度（按∠A、∠B和∠C是顶角时的三种情况分类讨论）。

学生的求异思维，难度在于解决数学问题时的思维淤堵。设置的题目采取梯度形式，如本例，从基础到变形1再到变形2，步步加深，在避免习题“一览无余”的同时始终以一种“惯性”牵引着学生解决问题中的思维。这种促进以学生主动参与学习辅以教师指导为学习方式，设置最近发展区，诱导求异，畅通思维，避免淤堵，形成了一种有利于再创造的求异思维情境，在无形中减轻了学生的学习负担。

二、典型知识题组化，串珠成络，构建多端思维，提高求异能力

数学问题的求异能力，不仅需要学生有相当的知识积累，而且能将这些知识在大脑中按自己特定的而又是科学合理的方式储蓄，构建的多端集中思维能在知识应用时自由地选择、提取、组合。在初中数学课堂教学中，教师将重要的、典型的知识题组化，串珠成络，帮助学生解决问题思维的多端出击，不仅便于学生发现和接受新知识，更能方便学生疏通、排查，提高其求异能力，从根本上减轻学生的学习负担。

【例2】 关于非负数的题组，使非负数的性质展现无遗。

（1）若8-x+x-8=0，求x。

（2）如果|x+1|+y+3+（z-4）²=0，求x+y+z的值。

（3）计算-x|x|+5x²。

（4）已知|x-2|+（xy-2）²=0，计算1xy+1（x+1）（y+1）+1（x+2）（y+2）+1（x+3）（y+3）+…+1（x+2022）（y+2022）的值。

由上面例子可知：把零散的知识按一定解题规律串成网络状，形成了良好的知识组块，有利于学生在数学问题的解决过程中产生多端的思维向认知结构的同化迈进，是减轻学生认知负担的有效方法，也是促进学生形成求异思维的必要条件。

三、探究方法多样化，百花齐放，引发灵动思维，增进解题活力

初中学生注意力高度集中的时间短，半节课后就会出现疲劳症状，效率下降;还有，初中学生的成就欲不高，稍有成就就容易表现出满足状，这是形成数学“两极分化”的原因之一。如果能经常要求学生做到一题多解，采取独立思考与两人小组（四人小组）讨论相结合的方式，有启发、有争论，有效地转换大脑兴奋点，激活脑细胞，实现多角度多方位地观察、归纳、猜想，就能增加解题活力，也能减轻学生的学习负担。

【例3】 如2022年4月本校“学情诊断”七年级期中数学第16题：已知9x=25y=15，则代数式（x-1）（y-1）+xy+3的值是________。

对七年级学生而言，这个题目是有点难度的，多数学生初看此题感觉一时无从下手，但在经过短暂的自虑、讨论，很快有同学根据性质“若a≠0，ax=ay，则x=y”得到方法一：

由已知得3²x=5²y=3×5，∴3²x-1=5，5²y-1=3，∴（5²y-1）²x-1=5，∴（2y-1）（2x-1）=1，∴x+y=2xy，∴原式=2xy-（x+y）+4=4。

接着，灵动的思维出现了。据此，很快有同学类推，得到方法二：

由已知得3²x=5²y=3×5，∴3²x-1=5，5²y-1=3，∴（3²x-1）²y-1=3，∴（2x-1）（2y-1）=1，即x+y-2xy=0，∴原式=2xy-（x+y）+4=4。

到这里，学生的思维更加活跃，有学生提出，既然有性质“若a≠0，ax=ay，则x=y”，那么可否得到“若a≠0，amx=amy，则mx=my，即x=y”这样的结论？老师当即指出，这里要增加“m≠0”这个条件;于是又有了方法三：

设9x=25y=15=axy，则9=ay，25=ax，又∵ax+y=ax·ay，∴ax+y=9×25=15²，又∵axy=15，∴a²xy=15²，∴ax+y=a²xy，∴x+y=2xy，∴原式=2xy-（x+y）+4=4。

这里的一题多探，不但激活了与问题相关的各知识点，而且学生通过活跃的观察、尝试、猜想等活动，在目的性、相似性、和谐性和批判性等指向原则指导下，形成解决问题方法的宏观判断，实现了学生已有知识、经验与问题情境的同化，不仅提高了问题探索的兴趣，增加了解题的活力，而且减轻了学生学习的畏惧心理。

四、呈题训练三步化，鼓励猜想，诱导精细思维，凝聚参与动力

数学的猜想是诱导学生精细思维的极好途径，是思维登高的梯子。笔者对解题训练按“读、讲、解”三步施行，诱导学生人人参与，使得学生个个都是学习的主体。

读题：全体学生一起读题，理解题意。从已知条件结合图形，一步一步探究，寻找隐含条件，分门别类列举在屏幕（黑板）上。

讲题：四人（两人）小组讨论，大胆猜想，大步骤思维、判断，选择解题方向，同时发挥优等生的“领头雁”作用，调动困难学生的思维积极性，共同探讨解题途径，制订解题策略。

解题：根据逻辑性和严密性原则，各人用数学语言表达完整的解题过程、方法。

【例4】 已知AB是⊙O的直径，C是AB延长线上的任意一点，CD切⊙O于D，DE⊥AB于E，求证：∠EDB=∠CDB。

读题（把重点内容、关键词画线或板书）：

（1）AB是⊙O的直径，若连接AD，则△ABD是直角三角形。直角三角形中两锐角互余、勾股定理、射影定理能否使用……

（2）CD是⊙O的切线，那么切线性质……、弦切角性质……

（3）CD是切线，CA是割线，那么切割线定理……

（4）弦DE⊥直径AC，那么垂径定理……

讲题（大胆猜想，穷举可能）：

生1：连接AD，则DE是Rt△ABD斜边上的高线，得出∠A=∠EDB，又由CD是圆的切线得∠A=∠CDB，∴∠EDB=∠CDB。

生2：连接OD，∵OD=OB，∴∠ODB=∠OBD，由CD是圆的切线得∠ODB与∠CDB互余，而∠OBD与∠EDB互余，∴∠EDB=∠CDB。

生3：延长DE交⊙O于F，连接BF，则由垂径定理得∠EDB=∠EFB，而由切线CD得∠CDB=∠EFB，∴∠EDB=∠CDB。

生4：过点B作⊙O的切线BM与CD交于M，则MD=MB，∴∠DBM=∠CDB，又∵DE∥MB，∴∠EDB=∠DBM，∴∠EDB=∠CDB。

生5：过点B作BN⊥CD，连接OD，则BN∥OD，∴∠ODB=∠DBN，而∠ODB=∠OBD，∴∠OBD=∠DBN，∴∠EDB=∠CDB。

解题：由学生自行完成（略）。

实行“读、讲、解”三步式析题，改变了老师说、学生听或者是优等生说、学困生听的局面（对数学成绩欠理想的同学，能说上一句、一点，都是进步，都可得到表扬）。人人参与题目的解读，集思广益，在参与过程中加强了学生思维的开放性和探索性，使学生的求异思维得到发展，个体参与的动力得到了凝聚与培养。

五、展示数学美丽化，陶冶情操，激活新颖思维，驱发内部学力

大千世界，数学花园风景独异，教师在课堂上有意识地展示数学美，能给学生一种数学学习的享受感，使学生内心有一种“想要学”的欲望。

例如，初三几何中的“黄金分割”是数学美的典型，而三角形的“四心”更是数学美的体现：

内心：三角形三内角平分线的交点;

外心：三角形三边垂直平分线的交点;

垂心：三角形三边的高线的交点;

重心：三角形三边的中线的交点。

爱美之心人皆有之，教师在讲解类似的题目时，不可单纯地为了解题而讲题，应极力地渗透数学的美，激活学生的新颖思维，陶冶学生美的情操：

再看下面这组填空题，在空格处填以下4个之一：内心、外心、垂心、重心：

（1）锐角三角形的内心是它的切点三角形（即三个切点所组成的三角形）的________心;

（2）锐角三角形的外心是它的中点三角形（即三边的中点所组成的三角形）的________心;

（3）锐角三角形的垂心是它的垂足三角形（即三边高线的垂足所组成的三角形）的________心;

（4）锐角三角形的重心是它的中点三角形（即三边的中点所组成的三角形）的________心。

学生进行分析：

（1）因为三角形的内心是其内切圆的圆心，D、E、F为切点，如图1，则OD=OE=OF，根据定理“到一条线段的两个端点的距离相等的点在这条线段的垂直平分线上”得：O点在线段DE、EF、FD的垂直平分线上，故O点是△DEF三边的中垂线的交点，故O点是切点△DEF的外心。