核心素养背景下初中数学建模素养培养策略分析

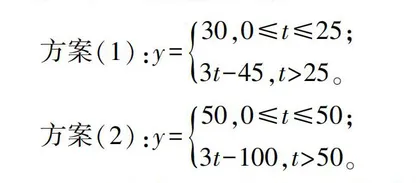
摘 要：从数学教育的整个发展历程来看，数学应用始终为关键性任务。有关数学建模，其是数学和现实生活有机结合的重要桥梁，一方面为针对现实问题实现数学化抽象，另一方面则呈现出综合水平更高的素养能力。而数学建模思想在增强实践能力、自学能力的基础上，助力核心素养的提升。尤其在核心素养背景下，初中数学课堂进行数学建模素养的培养及教学，显得至关重要。为此，文章立足初中数学课堂，重点探讨培养数学建模素养的具体方法。

关键词：数学建模素养；核心素养；培养策略；研究分析

中图分类号：G633.6 文献标识码：A 文章编号：1673-8918（2022）48-0066-05

作者简介：贾莉（1981～），女，汉族，甘肃庆阳人，甘肃省白银市平川区魏家地学校，研究方向：初中数学教育教学。

一、引言

依据学生需求形成的核心素养框架，各门学科也制定出相应的学科素养，而数学建模则是构成核心素养的关键部分。数学建模主要指的是将问题数学化，为问题的分析及处理提供基础。基于此，初中数学教师应积极引导学生思考，将初始的形象思维朝着抽象思维顺利过渡，帮助学生提高问题处理能力。数学建模在初中阶段的数学教学中也是一个重点内容，从实际情况来看，很多学生未能形成数学建模素养，因此应采取针对性的培养策略，提高其数学建模素养。

二、核心素养背景下数学建模素养构成要素

（一）建模知识

所谓建模知识，主要指的是学生认知建模，以及参与建模活动所需的知识。针对建模认知方面的知识，主要和建模相关的案例知识，而建模活动包含的数学知识属于基础性的建模知识。通常建模知识是由案例知识和基础性知识组成的。

（二）建模能力

所谓建模能力，主要指的是问题数学化，建立合适的模型求出模型的解，将解放回到原题检验，解释或是解决问题所需的能力。结合数学建模的具体要求，建模能力由以下几方面组成：阅读理解、计算、逻辑推理以及数学化等。

（三）建模思想

建模思想不仅是对知识的实质性理解，也是从理性角度出发理解数学规律，在数学内容以及认识中形成的数学观点。其能在学生的认知过程中反复利用，帮助学生建立通过数学知识处理问题所需的指导思想，具体包含模型、统计、分类以及化归思想等。

三、核心素养背景下培养数学建模素养的基本原则

（一）因材施教

关于数学建模素养的培养及思想渗透，属于逐渐提升和循序渐进的一个过程。因为不同学生在思维水平、知识储备、解题习惯等方面均存在一定差异，所以针对层次不同的学生，应该分析他们的实际接受能力，尽量选择学生可以普遍接受的方法，至于能力相对薄弱的学生可以单独提供指导。初中数学建模教学，并非仅是培养学生的应考能力，而是要促进学生技能、知识、思维等方面的综合发展。通过建模锻炼学生对实际问题的解决能力。教师通过进行因材施教的教学，也就可以更好地对学生数学建模素养进行培养。

（二）科学性

在初中数学核心素养的指导之下，要想对学生的数学建模素养进行提高，需要教师遵循科学性的原则，使得学生在数学建模的过程当中可以得到相关能力的发展。教师在教学过程当中，若能够保证更加科学，也就可以更好地对学生建模素养进行培养，使得课堂教学的质量更高。事实上，教师在实际进行教学的过程当中，所运用的方法都需要结合学生的实际特点来展开课堂的教学设计，并且进行科学性的数学建模，使得学生可以在教师的引领之下拥有建模的思想，提高自身的思维水准。因此，教师也就需要加强进行科学的建模教学。不仅如此，教师也需要注重进行科学性的评价，使得学生可以在数学建模的过程当中不断进行反思，发现建模过程当中存在的问题，及时采取相应的方法进行调整，帮助学生实现数学建模素养的提高。

（三）活动性

学生对数学知识进行学习的过程当中，仅仅对其进行理论知识的灌输无法使得学生得到更加长远的发展，因此，教师也就需要积极开展实践活动，使得学生可以在活动中实践，在实践中不断提高自身的建模素养，在实际对问题进行解决的过程当中，可以积极建模，以更好地对实际问题进行解决。针对有关折叠、测高等一些实践性探索课题，教师可以改变单向灌输、做习题等传统模式，而是组织学生在课外活动中，通过动手、动脑敢于创新，在积极探索的同时表达个人思想，增强沟通合作能力。学生通过进行数学建模实践，也就可以对数学知识加以总结，在脑海中形成数学建模体系，进而实现对学生数学建模素养的培养。

（四）创造性

教师在实际对初中生进行数学建模素养的培养时，需要发挥出创造性能力，遵循创造性的原则。而教师首要的任务就是对传统的教学观念进行创新，真正做到与时俱进，获得更加先进的教育理念，使得学生可以在更加高效的课堂教学当中，提高数学建模的素养。其次，教师需要注重对建模的教学方法进行创造。通过对不同的教学方法加以应用，进而对学生进行培养，使得学生可以从多个角度对数学建模的思想加以体会，以此进行数学建模，提高实际的建模学习效果。最后，教师需要指导学生发挥出创造力，在实际进行学习的过程当中，运用不同的学习方法，形成更加正确的建模思维，善于动脑，提高学生的数学建模素养。总之，教师需要清楚认识到，教学的核心价值在于推动学生创造力的发展。而建模教学在创造思维、创新意识等方面起到一定的促进作用。在课堂教学中，要求教师能富有创造性地设计数学建模素养培养方案，挣脱传统思维桎梏，为建模思想的有效渗透创造条件。

（五）主体性

教师在培养学生数学建模素养的过程中，还应该遵循主体性原则，对课堂教学中的主体加以明确，进而实现学生数学素养的提升。而实现这一原则的关键就是需要教师更加精准地进行自身定位。也正因为现阶段的初中数学教师没有注重发挥出学生的主体地位，错误地认为自己是课堂中的主体，使之在教学时更加注重依据教学任务开展教学，并不会对学生基本学习状况加以掌握，很难运用针对性的方法对学生建模思想进行培养，导致实际的课堂教学效果不容乐观，阻碍学生综合素养的发展。而在数学建模素养的培养中，教师只有突出学生的主体性，以及自身的指导性，才可以使得学生更加积极以及主动地参与到数学建模的学习当中，主动进行数学的建模，提高学生的数学建模素养。而在这一过程当中，教师也需要对学生进行指导，发挥出引导者的作用，进而使得学生可以在教师的引领之下，得到更进一步的提升。

四、初中数学建模素养培养的意义

对数学建模素养来说，其属于数学核心素养中的重要内容，与新课程的改革方向相一致，可以对学生的思维进行拓展，使得学生的综合能力得到发展。事实上，人的大脑会蕴含十分丰富的知识，最重要的就是需要开发以及利用。而对数学建模素养而言，正是对学生大脑进行优化的主要手段。学生在学习的过程当中，通过进行建模，也就可以解答更多难理解的问题，使得学生更易掌握知识。而且，数学建模也会使得教师对不必要的教学环节加以减少，使得课堂氛围更加热烈，提高教学的效果。由此可知，无论是对学生还是教学来说，数学建模都是十分关键的。

五、数学建模主要步骤

（一）找出并发起问题

数学教师需能引导学生学会思考，主动找出并且可以发起问题。这属于数学建模的第一个环节。需要注意的是，问题的找出及发起必须依托具体的情境，就教学情境或者现实生活场景展开深入思考，其中发起问题属于抽象性的数学问题、现实问题等，有关这一环节发挥关键作用的是提出问题，要求问题需具有一定的思考探讨价值，也只有依据某一或是系列问题，才能进行建模。

（二）问题分析与建模

实际上，分析问题不需要拘泥于数学方面，也需要调动一些生活经验或者是其他学科知识，而在有些时候可能涉及资料差异。这一过程就是对所提出的问题加工，也就是“问题数学化”，转化为一道数学问题，虽然带有不同的现实背景，可是在内部关系上从属于数学层面。其中“再加工”，则是通过已掌握的定理、概念和性质把问题模型化。在上述环节中实现数学抽象，从而现实世界真正进入数学世界，依托数学的规律及方法分析问题。

（三）明确参数与求解

其主要指的是解决问题的过程，而明确参数为重中之重，核心基础是数据质量及其丰富性，那么收集数据便是构建数学建模的主要部分。为此，应确保数据来源的多样性，以封闭问题为例需要使用已有数据，至于开放性问题，通过网络或是教材等途径获得数据。利用数据确认模型所涉及的各项参数，通过计算解决这道问题。由此，可以清楚看到数据分析、数学运算、数学建模的密切联系。

（四）检验结果优化模型

通常截至上个步骤就能得出结果或是有效判断。但是一些问题相对复杂涉及方面较多，模型有可能涉及类型不同的参数，导致计算使用的数据来源相较单一，有可能结果发生偏差，为此需要结合具体情况进行调整。

六、核心素养背景下培养数学建模素养的相关策略

（一）通过问题意识培养数学建模思想

在进行数学学习时，学生在面对部分数学问题时不可避免会陷入困境，可若能积极思考便能形成问题意识，而通过发挥问题意识的作用，有助于学生主动进行学习探究，敢于提出问题并独立分析、解决，这对数学建模素养的培养至关重要。那么，数学教师应为学生提供便利条件，创设合适的问题环境。这是因为借助问题情境有利于数学问题意识的激发，引导学生主动参与，并在相应的问题情境中找出问题。与此同时，创设问题情境应密切结合学生现实生活，不仅要满足学生认知水平，还能激发学生的学习积极性。例如“上网收费方式选择”的生活问题，教师可将其整合成数学建模问题。同学A家有三种可选择的上网收费方式：（1）每月30元、包时上网时间25小时，超时费用每分钟0.05元；（2）每月50元、包时上网时间50小时，超时费用每分钟0.05元；（3）每月120月、包时上网时间不限时。通过小组讨论选择最合适的一个上网收费方式，学生重点讨论（1）（2）收费方式且其数量关系如下：

然后组织学生将这道问题描述为函数问题，通过函数模型转化成现实问题。假设上网所用时间是t小时。方案（1）需要缴纳的上网费用是y₁元，方案（2）需要缴纳的费用是y₂元，方案（3）需要缴纳的上网费用为y₃元，那么：

将问题转化成对比这三个函数的大小，学生选择通过方程或是不等式的方式求解y₁>y₂，y₁=y₂，y₁<y₂时t的值。可是因为y₁、y₂均为分段函数，如果利用不等式进行求解较为烦琐，借此引导学生通过函数图像求解。具体如下，A：0≤t≤50，y₁、y₂函数图像存在一个交点，求解该交点的横坐标，也就是y₁=y₂的情况下，3t-45=50，t=3123。B：0≤t≤3123，y₁的函数图像位于y₂函数图像之下，也就是y₁<y₂，那么方案（1）比方案（2）更省钱。C：t>3123，y₁的函数图像位于y₂函数图像之上，也就是y₁>y₂，那么方案（2）比方案（1）更省钱。D：t>50，函数y₁、y₃存在一个图像交点，将该交点的横坐标求出，也就是y₂=y₃，3t-100=120，t=7313。E：t>7313，y₂的函数图像位于y₃函数图像之上，也就是y₂>y₃，那么方案（3）比方案（2）更省钱。在这道问题的解题过程中，不仅培养了学生的数学建模素养，还锻炼了其对问题分析及处理能力，有利于学生体会方程和函数相结合的数学思想。

（二）依据“循序渐进”原则培养数学建模素养

很多学生在设计建模问题时往往显得缺乏信心，教师则需在建模教学初期，引用精心选择的现实问题。挑选相对容易，密切联系生活且有趣的题目，引导学生构建简单的数学模型，这样能为学生处理复杂的数学题目树立信心。以“一元一次方程”为例，教师可引入这一问题：已知某件童装的价格为150元，因为商场店庆降价为八折出售，但是商家依然获利20%，试求服装进价为多少。对这道方程问题，首先引导学生将问题中的关键量提炼出来，然后依据（售价-进价）进价=利润率构建等量关系。假设童装进价是x元，列出方程150×0.8-xx=20%，解得x=100。打折销售的问题和学生日常生活较为贴近，学生会对其产生一定兴趣，至于有的学生不了解利润率或是利润等概念，教师可以事先让学生利用不同途径搜索答案，相比将定义直接给出能获得更理想的教学效果。然后引入稍有难度的问题，进行能力拔高。例如某工厂采购60箱单价为80元的原材料，该厂A号和B号车间使用其进行染色剂的生产。A号车间使用1箱原材料和4吨水能出产12千克染色剂；B号车间因为使用节能技术，降低耗水量50%，而且B号车间的产出效率和A号车间相比少2千克。染色剂市场售价是每千克30元，水费每吨5元。该工厂为响应国家号召，用水总量要不超过200吨。尝试为该厂设计合理的生产规划，在不超过用水要求的基础上获利最多；预算获利的最大值。因为学生已经初步理解利润及利润率概念，那么解题关键是利润=总售价-材料成本-水费。为此，假设A车间使用x箱材料用于染色剂生产，那么B号车间使用的原料为（60-x）箱，可得A车间一共耗水4x吨，B车间为2（60-x）吨，A车间生产的产品总量为12x千克，B车间则是 10（60-x）千克，A、B车间总共的产品售价是30［12x+10（60-x）］元，如果可得的最大利润是W，列出式子：W=30［12x+10（60-x）］-80×60-5［4x+2（60-x）］=50x+12600；因为工厂的用水总量不能超出200吨，所以4x+2（60-x）≤200，x≤40，即A车间使用40箱原料生产染色剂，能够获得最大利润，也就是14600元。