小议第二学段数学读物整本书阅读策略

当前语文学界对整本书阅读的研究和实践如火如荼，教学走出课堂，走进课外书籍后，再回归课堂，成为普遍的现象。那么数学学科是否有必要引以为鉴？具体应该怎么做？针对这些问题，笔者拟以罗勃·伊斯特威与杰里米·温德姆合著的《三车同到之谜》为例，略行探讨，以作商榷。

一、抛砖引玉——鼓励学生走进数学读物

数学学科少有教师做整本书阅读教学的研究，这是由数学教学本身的语言属性决定的。一方面，数学语言拥有与语文不同的文字、文法与句法，不同的数学规律之间的数学语言可以不相关，这使数学呈现出相对的独立性。另一方面，《义务教育数学课程标准（2011年版）》针对第二学段的教学指出，应“尝试从日常生活中发现并提出简单的数学问题，并运用一些知识加以解决”。这指向了数学的现实性意义，教材中“综合与实践”部分旨在推动数学规律在生活情境中的具体运用，彰显了教学回归生活的倾向。也就是说，从生活中发现数学是培养学生数学思维的优质土壤。在《三车同到之谜》这本书中，描绘生活中的数学现象，阐述作者发现和总结的数学规律。这种同时具有数学思维和生活逻辑的数学读物，便可视为数学学习的有益组成。

二、授人以渔——挖掘《三车同到之谜》教学价值

数学读物将数学知识置于生活场景之中，它显示的是生活与数学的连接，但它不是纯粹的数学语言，更多是一种数学思维方式。教师在教学中，应有意识地渗透整本书阅读策略，授人以渔，鼓励学生回归生活，以数学的思考方式寻找、提炼数学规律。如封面所载的各种问题，汇集数学读物一般性特点的同时，妙趣横生。此读物的教学价值在于可以引导学生品味数学的乐趣和美，还可以借其管窥数学读物这一类书籍的阅读策略。

三、由浅入深——探究《三车同到之谜》阅读策略

数学有着自己的特征，那就是精确、清晰以及范围限定，在此基础上，笔者将从三个方面阐述《三车同到之谜》的阅读策略。

1. 阅读正文之外的内容。

封面、序、导言和目录均载有书的信息和解读密码，注意这些细节有助于理解书的内容和框架。

（1）封面。

本书封面紧扣“趣味”这个主题，公交司机和乘客各自不同的生动表情、巨大的花朵和绿叶都极富生活气息，同时到达的三辆10路公交车点出了书名， “迷人”“有趣”“日常生活中的数学”等文字，指向书的可读性，也提示内容的源头——生活。

（2）序和导言。

序和导言讲述了作者对数学和本书创作的一些观点和看法。例如，“我们不是发明数学，而是发现数学。”提示了数学与人的关系，即数学学科关乎人对事物的探索，《三车同到之谜》的创作基础在于作者对生活的数学思考。读出这些观点和看法，有助于在阅读过程中了解作者的写作逻辑。

（3）目录。

从封面了解书的大致风格，从序和导言中看到作者的数学理念，接下来可以通过目录窥见书的枝脉。阅读目录，不能一读了之，应当大胆质疑、小心求证。例如，当看到类似“为什么我总是在交通阻塞中？”的章名时，也许我们会想到自己经历过的在公路、自动扶梯和超市等场合中令人焦躁而无奈的排队场景。关注此类信息，可以引导学生思考，进而引导学生探测。

2. 阅读正文。

（1）读最感兴趣的章节。

《三车同到之谜》的一个特点是不同章节涉及不同的主题。读目录时，需要带上“这个问题的答案我也想知道！”“到底是怎么回事？”的好奇心，找出自己最感兴趣的章节。有的人可能在意目录中的“我该走哪条路”，有的人可能想知道目录“这是谁干的？”中的具体内容。无论读者在意什么，翻开自己想要了解的章节进行阅读。

（2）跳读快速找到问题的答案。

读数学读物，只需要找到其中的数学关系。也就是说，我们不需要过分在意故事的要素（即时间、地点、人物等）是否真实存在，也不需要关心作者受困扰的具体情感描述，只需要了解作者如何提问题，如何寻找答案。每一章节，作者都会聚焦几个关键数学问题，因此可以考虑以跳读的方式寻找基础问题的答案。以第10章为例，我们可以一边跳读，一边回答下列问题：①作者的好奇和疑惑是什么？分正多边形蛋糕时，我们很容易切出2块、4块或8块，可是如何切出奇数块蛋糕呢？②涉及的数学关系是什么？三角形面积的公式：面积=底×高。由于每一块蛋糕的高相同，体积只与三角形面积相关，因此从蛋糕中心出发，将周长等分后，得到的蛋糕体积相等。③怎样利用数学关系来验证作者的好奇和疑惑？更换不同的多边形蛋糕，试着为不同数量的人切蛋糕，检验你的结果。④有哪些意外情况？不规则的形状，难以适用。

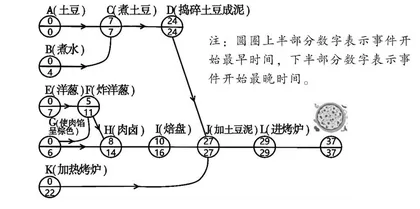
（3）精读图表。

数学读物的精彩之处，还在于语言之外提供了另一种表述方式——图表。本书中的图表不仅以有趣的方式展示了生活场景，如切蛋糕、淋浴、乘坐自动扶梯等，还描绘了生活中的数学，如植物中花瓣的数量、菠萝的螺旋线、苹果中星形和花芽的角度等神奇的数学关系。最后，图表也解答了一些数学现象，例如第18章中关键路径和其他程度问题的图表展示，见下图。

3. 引导学生对数学读物中的内容进行思辨。

数学读物的论述是思辨的过程。阅读时，要注意总结分析作者的发现模式。读完后，引导学生进行思辨，大致有三个方向：

（1）加强作者得出的结论。找到生活中可以支撑作者论述的例子，或者验证其他的一些数学关系。以第17章为例，提到狐和兔数量变化关系，除此之外还可验证其他不同的动物关系组合，如澳大利亚政府为保护袋鼠猎杀了狼，袋鼠的数量随之呈指数增长，但如果狼不被猎杀，狼和袋鼠的数量关系将出现与狐和兔类似的变化曲线，数学规律依然适用。

（2）质疑作者得出的数学规律。很少人想过证明书中的数学规律正确与否，或数学家们如何得出它们，然而数学却需要培养这样的质疑精神。那么，是否还有作者没有提到的新的前提？该前提会不会不符合本文的数学逻辑？

（3）参照本书中的模式，找寻生活中的数学。数学读物阅读的最终目的不是记住数学规律，而是用数学的眼光看待生活，养成从自己好奇和疑惑的事情入手，经常性地发现和验证数学关系。

（作者单位：福州市鼓楼实验小学）