指向“学教评一体化”的数学问题解决教学模式的构建与实践

［摘 要］问题是数学的心脏，数学问题解决是一种重要的认知活动，数学问题解决教学蕴含全新的教学理念与价值诉求，其本质是师生学数学、用数学的过程。基于学习论、教学论和课程论三大理论的内涵挖掘，围绕数学问题解决教学的目标、任务、策略和评价四个方面，建构了指向“学教评一体化”的数学问题解决教学模式，并尝试将其应用于数学单元复习课教学，从操作层面进行实践检验。

［关键词］学教评一体化；数学问题解决教学模式；单元复习课

［中图分类号］    G633.6        ［文献标识码］    A        ［文章编号］    1674-6058（2024）05-0001-05

一、问题提出与模式构建

《普通高中数学课程标准（2017年版2020年修订）》（以下简称《课标》）的“课程目标”中提出，通过高中数学课程的学习，学生能获得进一步学习以及未来发展所必需的数学基础知识、基本技能、基本思想、基本活动经验（简称“四基”），提高从数学角度发现和提出问题的能力、分析和解决问题的能力（简称“四能”）［1］。问题解决已经成为贯穿《课标》的关键词和主题词，数学学科核心素养的形成与发展源于知识的应用与问题的解决。哈尔莫斯认为，问题是数学的心脏。波利亚把数学视为一门问题解决的学科，并把问题解决作为数学教学的焦点。围绕问题解决而开展的数学教学，既是数学教育的重要理念、策略和方法，也是数学教学的基本组织形式，其设计包括运用系统方法分析问题解决教学起点、确定问题解决教学目标、设计问题解决教学活动、选择问题解决教学策略、实施问题解决教学评价、修订问题解决教学方案等重要环节［2］，最终指向问题解决这一根本目标。

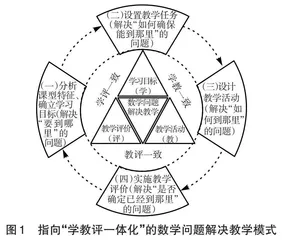
问题解决教学模式已经成为数学教育研究的重要范式。然而，研究发现，当下我国数学问题解决教学还普遍存在“课堂整体观照不足，重教学轻评价”“学习目标定位不准，重知识点轻达成度”“教学评价技术不熟，重判断轻改善”［3］等问题。究其原因是在教学中不能实现学习、教学、评价这三者的一体化。在我国，崔允漷教授最先引进“教学评一致性”这一概念，并从四个方面对其含义作出了解释，构建了“学教一致、教评一致、学评一致”三因素模型［4］。后来，章勤琼、阳海林等人提出“学教评一致性”概念，并主张课堂教学首先要分析好学生学习的内容与要求，才能更好地分析教师的教学和学习的评价［5］。相比“教学评一致性”，“学教评一体化”更符合《课标》的结构特点，也更符合教育教学实践的逻辑。通过深度解读指向“学教评一体化”的数学问题解决教学的本质内涵，以及探讨其从课标走向课堂、从理论走向实践的操作路径与实施策略，构建了指向“学教评一体化”的数学问题解决教学模式（如图1）。

数学单元复习课教学以问题解决为根本目标，强调基于“关键考查问题”“小问题”“具体问题”高考三大考查问题来设计问题链，与其相关的教学内容分析、学习目标确立、教学策略选择、教学评价实施都迫切需要实现学教评一体化。因此，基于指向“学教评一体化”的数学问题解决教学模式的数学单元复习课教学可以概括为以下四个基本环节：一是依据课程标准、核心素养、教材内容、高考三大考查问题，分析课型特征并确立学习目标，解决“要到哪里”的问题；二是依据学生的认知起点和已有的学习经验，剖析教学的重难点，并对确立的学习目标进行评估，解决“如何能到那里”的问题；三是依据确立的学习目标，设计具体的教学活动，解决“如何到那里”的问题；四是依据适切的评价框架，实施教学评价，解决“是否确定已经到那里”的问题。

本文以“平面向量数量积”单元复习课教学为例，探索指向“学教评一体化”的数学问题解决教学模式的构建与实践。

二、基本流程与实践操作

（一）依据单元复习课的课型特征，分析高考三大考查问题的考查要求，确立学习目标，解决“要到哪里”的问题

指向“学教评一体化”的数学问题解决教学，需要回答的第一个问题是如何确定学习目标，即“要到哪里”。相应的“学习目标”应具有“导教、导学、导评”的功能。对于“平面向量数量积”单元复习课教学，教师可通过前测，评估学生求解数量积的整体水平，并实施动态教学分析，以明确“要到哪里”，为教学活动的实施做好铺垫，让学生确定学习的目标、重点、难点，带着问题进行学习。“前测”的试题涉及定义法、基底法、坐标法、投影法和极化恒等式法。本环节围绕“平面向量数量积”这一高考关键考查问题设计了如下前测问题链：（1）已知[a=2]，[b=1]，[<a，b>=2π3]，求[a·b]；（2）在（1）的条件下求[2a-b]与[a]的夹角；（3）在[△ABC]中，[∠C=π2]，[AC=3]，求[AB·AC]；（4）已知[a=（x，-4）]，[b=（1，2）]，若[<a，b>∈π2，π]，求[x]的取值范围；（5）在平行四边形[ABCD]中，[AB=2]，[AD=1]，[E]为[DC]的中点，[AE]与[BD]交于点[M]，若[MA·MB=-49]，求[AB·AD]。

设计意图：围绕基础知识与基本技能，将零散、模糊和死板的问题整合成系统、清晰和灵动的前测问题链，为本节课复习与探究“关键考查问题”“小问题”“具体问题”热身，为知识的重构做好铺垫，明确“要到哪里”。“前测”问题的解决情况反馈，不仅可用于调整、优化本节课的学习目标，还可用于指导教学任务的分析和教学活动的开展。

（二）依据已确立的学习目标，设置“小问题”教学任务，解决“如何确保能到那里”的问题

指向“学教评一体化”的数学问题解决教学，需要回答的第二个问题是如何进行教学任务设置，即设置教学任务，解决“如何确保能到那里”的问题。在此环节中，基于5个“前测”问题，开展师生、生生互动交流，明确解决平面向量数量积问题涉及的知识、技能和方法，梳理出求解平面向量数量积的五种公式、四种方法，以及与之相关的两大上下位知识。本环节围绕“平面向量数量积”这一高考关键考查问题设计了如下“小问题”链：（1）在上述5个问题的解决过程中用到了哪些知识、哪些方法？你有什么体会？（2）结合平面向量数量积的公式及其结构特点，思考[a·b]与[a+b]、[a-b]的内在关系及其几何表达。（3）如果把问题（2）的代数关系迁移到三角形中，还可以怎么表示？三角形中线与数量积有何关系？

设计意图：围绕基本思想与基本活动经验，将浅层、低阶的学科认识问题整合成超越具体知识、体现学科本质、凸显专家思维的“小问题”链，目的在于对单元复习课中学生解决问题需具备的思想、方法进行提炼与加工，让学生运用知识时知其然，也知其所以然。根据“小问题”的解决情况反馈，调整课堂教学节奏，并优化下一环节中“具体问题”的解决教学。

（三）设计问题解决教学的基本事件，优化“具体问题”教学策略，解决“如何到那里”的问题

指向“学教评一体化”的数学问题解决教学，需要回答的第三个问题是如何进行教学策略的开发与选择，即分析指导教学任务完成的策略，解决“如何到那里”的问题。此环节的教学以“具体问题”链为中心，以教师为主导、学生为主体，依据“前测问题”“小问题”的解决与反馈，预设和生成“具体问题”链，确保预设问题是多重的、非线性的，生成问题是学生自主提出的且是自然的。在师生交互下产生的预设问题的呈现顺序、呈现跨度、呈现方式以及呈现内容应随课堂的即时反馈做出调整，追求自然生成。“平面向量数量积”问题的解决，需要掌握最基本、最常用的三大形式（定义式、基底式、坐标式）。要想解决“如何到那里”的问题，教师需要在教学中呈现样例，样例要有较强的针对性和互补性。本环节围绕“平面向量数量积”设计了如下“具体问题”链以及变式子问题链：

具体问题1：由两个确定元过渡到三个确定元：[AC·AE=（AB+AD）AB+12AD]。

（1）在正方形[ABCD]中，[AB=2]，点[E]为[BC]中点，求[AC·AE]。

具体问题2：掌握极化恒等式法求数量积，感悟整体法、方程思想、化归思想在问题解决中的应用。

（2）等边三角形[ABC]中，[AB=2]，[P]为平面[ABC]内一点，求[PA·（PB+PC）]的最小值。

变式1：在[△ABC]中，[D]是[BC]的中点，[AD=3]，[BC=10]，求[AB·AC]。

变式2：已知[AB]为圆[O]的直径，[M]为弦[CD]的动点，[AB=8，CD=6]，求[MA·MB]的取值范围。

变式3：平面四边形[ABCD]，[O]为[BD]的中点，[OA=3，OC=5]，[AB·AD=-7]，求[BC·DC]。

具体问题3：利用几何问题代数化思想，建立坐标系，将“平面向量数量积”动态问题转化为代数问题，感悟在利用坐标法解决“平面向量数量积”动态问题的过程中，正交与斜交的不同及相应问题的解决方法的差异。

（3）矩形[ABCD]中，[AB=2]，[BC=2]，[EB=EC]，[F]在[CD]边上，[AB·AF=2]，求[AE·AF]。

变式1：在[Rt△ABC]中，[CA=CB=2]，[M、N]是斜边[AB]上的两个动点，[MN=2]，求[CM·CN]的取值范围。

变式2：在[△ABC]中，[OM=1]，[ON=2]，[∠MON=120°]，[BM=2MA]，[CN=2NA]，求[BC·OM]。

变式3：在[△ABC]中，[D]是[BC]的中点，[E]在[AB]边上，[BE=2EA]，[AD]与[CE]交于点[O]，若[AB·AC=6AO·EC]，求[ABAC]的值。

设计意图：在探究“具体问题”链的过程中，设计具体、真实、综合的问题解决情境，给学生提供冷静思考的时间和充分表达的机会，引导学生像数学家一样思考问题、解决问题，有效落实了学生“四基”“四能”的培养，提升了学生分析和解决问题的能力。由问题解决与经验生长的共生共存关系可知，并不预先存在一种固定的方式使学生学会解决问题。学生需要在质疑与试错的过程中、聆听与被聆听的情境中、批判与反思的体验中建构个人的知识结构［6］。课堂教学，功在预设，贵在生成。根据课堂中学生的实际情况，教师应及时做出教学调整，在问题解决的过程中兼顾学生提出问题能力的培养。

（四）开展问题解决教学的评价反馈，评价“关键考查问题”教学效果，解决“是否确定已经到那里”的问题

指向“学教评一体化”的数学问题解决教学，需要回答的第四个问题是如何检测学习效果，即如何实施教学评价，解决“是否确定已经到那里”的问题。依托《课标》的课程内容要求和学业质量标准，通过课时对话、单元提炼、作业练习进行评价反馈，检测问题解决教学是否已经实现预期目标，检测学生是否已经掌握解决问题所需的基础知识、基本技能、基本思想，以及其提出和分析问题的能力是否得到锻炼，并通过评价反馈改进教与学。

1.从知识、方法、体验三个角度展开课时对话，夯基固本

（1）知识回顾：本节课，我们学到了哪些数学概念和公式？

（2）方法回顾：除了学到具体的知识，我们是否还掌握了一条研究平面向量数量积问题的路径？

（3）经历回顾：这节课我们经历了什么？

2.围绕“考查问题”“题胚”“变式”展开单元提炼，正本清源

（1）构建单元复习课教学的基本问题框架。基于指向“学教评一体化”的数学问题解决教学模式，围绕“关键考查问题→小问题→具体问题”构建“平面向量数量积”单元复习课问题解决教学的基本问题框架（如图2）。

（2）提炼高考关键考查问题的模胚。基于指向“学教评一体化”的数学问题解决教学模式，关注立意、情境、设问三大命题要素，总结提炼出关注平面向量数量积问题的题型结构及试题模胚。

已知：向量（三角形、四边形）的模长（与模有关的等式）、夹角、点（动点）、坐标。

求解：某两个向量的数量积的值（范围）。

（3）实施高考关键考查问题的变式。基于指向“学教评一体化”的数学问题解决教学模式，从问题表征角度归纳总结平面向量数量积问题的题型结构（题胚），并从问题变式角度归纳总结平面向量数量积问题的考查特点，以归纳解题的一般方法，获得解决此类问题的高级规则和图式。