多维联想　有序思维　聚焦方向

［摘 要］解题不是方法的简单堆积，而是发散思维的呈现，是灵活运用知识的体现。解题能勾勒出知识之间的联系，深化学生对数学思想方法的认识。文章对基于TPACK框架和分层教学理论的解题教学进行探索，具体从求线段的视角对一道联考题分别提出7种解题方法。

［关键词］TPACK框架；分层教学理论；解题教学

［中图分类号］    G633.6        ［文献标识码］    A        ［文章编号］    1674-6058（2024）17-0007-03

在解题教学中，教师不仅是学生学习活动的参与者和观察者，还是学生学习活动的管理者。通过管理学生的学习活动，教师可得到学生的学情反馈，并不断完善整个管理系统的分层结构。通过运用信息化技术，教师还可以实现解法分层、作业分层以及学生分层合作学习等。

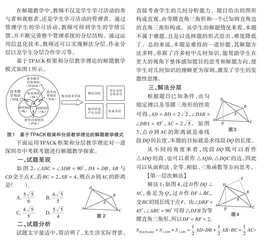
基于TPACK框架和分层教学理论的解题教学模式如图1所示。

下面运用TPACK框架和分层教学理论对一道深圳市中考联考题进行解题教学探索。

一、试题呈现

如图2，[∠ABC=∠ADB=90°]，[DA=DB]，[AB]与[CD]交于点[E]，若[BC=2]，[AB=4]，则点[D]到[AC]的距离是（ ）。

A. [556] B. [655]

C. [455] D. [554]

二、试题分析

试题文字量适中，简洁明了，无生活实际背景，直接考查学生的几何分析能力。题目给出的图形构成直观，由等腰直角三角形和一个已知两直角边的直角三角形构成。从学生的解题情况来看，本题不属于难题，且是以选择题的形式给出，难度降低了。总的来说，本题是难得的一道好题，其解题方法多样，串联了许多初中几何知识，能帮助学生在更大的视角下整体感知题目的思考和解题方向，使学生对几何知识的理解更为深刻，激发了学生的发散性思维。

三、解法分层

根据题目已知条件，由勾股定理以及等腰三角形的性质可得，[AD=BD=22]，[∠DAB=∠DBA=45°]，[AC=25]。如图3，点[D]到[AC]的距离就是垂线段[DQ]的长度，本题的目标就是求线段[DQ]的长度。

从不同的角度来看，线段[DQ]既可以看作[△ADQ]的高，也可以看作[△AQD、△DQC]的边，因此可以从面积法、全等、相似、三角函数等方向思考。

【第一层次解法】

解法1：如图4，过[D]作[DQ⊥] [AC]，垂足为[Q]，过[D]作[DF⊥BC]，交[BC]的延长线于点[F]。由[∠DBF=45°]，[∠ABC=90°]可得[△DFB]为等腰直角三角形，所以[DF=BF=2]。[S四边形ADBC=S△ADB+S△ABC=12AD·DB+12AB·BC=12AC·DQ+12BC·DF=12×22×22+12×2×4=8]。于是[12AC·DQ=8-12×2×2=6]，所以[DQ=655]。

解法分析：作[△DAC]的高[DQ]，而[AC]的长度已知，如果[△ADC]的面积已知，则[DQ]作为[△ADC]的高可求。四边形可以看作由两个直角边已知的直角三角形拼接而成，它的面积是可求的，也可以看成是由[△ADC]和[△DBC]拼接而成。[△DBC]的面积可以通过以[BC]为底来求，于是延长[BC]，构造等腰直角三角形[△DFB]，得到对应的高。

解法2：如图5，取[AB]的中点[G]，连接[CG]，并延长[CG]交[AD]于点[H]，所以[AG=BG=BC=2]，则[△BGC]为等腰直角三角形，所以[CG=DB=22]，[∠DBA=∠BGC=45°]，[∠AGC=∠CBD=135°]，因此[△AGC ]≌[△CBD]，[DB]∥[CH]，且[HG=12DB=2]，又[CD=AC=25]，[CH⊥AD]，于是[S△ACD=12AD·CH=12×22×32=6=12AC·DQ]，所以[DQ=2×6AC=655]。

解法分析：考虑[△DAB]为等腰直角三角形，以及[BC=12AB]，可以取[AB]的中点，构造全等三角形，得到[△CDA]为等腰三角形，[DB]∥[CH]，从而求出[CH]的长度，它也是[△CDA]的高，利用等面积法可求出[DQ]的长度。

【第二层次解法】

解法3：如图6，过D作DQ⊥AC，过[B]作[BJ⊥DQ]，[BK⊥AC]，垂足分别为[Q]、[J]和[K]。在[Rt△ABC]中，[AC=AB2+BC2=42+22=25]。因为[S△ABC=12AB·BC=12BK·AC=4]，所以[BK=455]。在[Rt△BAK]中，[AK=AB2-BK2=855]。易证，四边形[JBKQ]为矩形，[△DAQ ]≌[△BDJ]，所以[DJ=AQ]，[DQ=BJ=QK]，[JQ=BK=455]。设[DQ=JB=QK=x]，则[DJ=AQ=x-455]，所以[AK=AQ+QK=x-455+x=855]，所以[DQ=x=655]。

解法分析：[△ADB]为等腰直角三角形，有一组边相等，可用同角的余角相等，从全等条件分析，可构造[△DAQ ]≌[△BDJ]，所以[DQ=BJ]，将未知的量转换为已知量。于是，过[B]作[BK⊥AC]，得到矩形[JBKQ]，这样[DQ=BJ=QK]，再根据线段之间的关系，可求出[DQ]的长度。

解法4：如图7，过D作DQ⊥AC，垂足为[Q]，过[B]作[BM⊥AC]，垂足为[M]，延长[QA]至点[D']，使得[D'Q=DQ]，延长[MC]至点[B']，使得[MB'=MB]。易得[△D'DQ]和[△BMB']为等腰直角三角形，所以[∠DD'Q=∠BB'M=∠DAB=45°]。由解法3可得，[BM=455]，[AM=855]，所以[AB'=1255]。根据“三角形内角和为180°”和“平角为180°”可得[∠D'DA=∠BAB']，所以[△DD'A ]∽[△AB'B]，所以[DAAB=DD'AB'=22]，所以[DD'=1255×22=6105]，所以[DQ=6105×22=655]。

解法分析：考虑[∠DAB=45°]， 在直线[AC]上构造两个[45°]，利用三角形内角和与平角度数可以得到[△DD'A]与[△AB'B]相似，同时还可以得到[△DD'Q]为等腰直角三角形，利用相似比以及等腰直角三角形的边的比例关系可求出[DQ]的长度。

【第三层次解法】

解法5：如图8，过D作DQ⊥AC，垂足为[Q]，过[D]作[RS]∥[AC]，过[A]作[AR⊥AC]交[RS]于点[R]，过[B]作[BT⊥AC]，延长TB交[RS]于点[S]，交[AC]于点[T]。易得四边形[RDQA]、四边形[DQTS]、四边形[RSTA]均为矩形。因为[∠ADB=∠ARD=∠DSB=90°]，所以[∠RAD+∠RDA=∠RDA+∠BDS=90°]，于是[∠DAR=∠BDS]。又因为[AD=DB]，所以[△ARD ]≌[△DSB]，所以[RD=SB=AQ]，[AR=DQ=ST=DS=QT]。由解法3可得[BT=455]，[AT=855]，设[DQ=RA=DS=QT=ST=x]，则[SB=AQ=RD=x-455]，所以[AT=AQ+QT=x-455+x=855]，所以[DQ=x=655]。

解法分析：此解法与解法3有相似之处，同样借助等腰直角三角形的特征，构造全等三角形，进一步构造矩形，得到边与边之间的数量关系，借助方程思想求出线段[DQ]的长度。

解法6：如图9，过D作DQ⊥AC，垂足为[Q]，过[B]作[BV⊥] [AC]，垂足为[V]，过[D]作[DX⊥AB]，垂足为[W]，交[AC]于点[X]。因为[△DAB]为等腰直角三角形，所以[DW=AW=BW=2]。又因为[∠ABC=90°]，所以[WX]∥[BC]，所以[WX=12BC=1]，所以[DX=DW+WX=2+1=3]。由解法3可得[AV=855]。因为[∠AQD=∠DWA=90°]，所以[∠BAV=∠XDQ]，所以[△BAV ]∽[△XDQ]，于是[DQAV=DXAB]，因此[DQ=AV·DXAB=855×34=655]。

解法分析：考虑[DQ⊥AC]，利用对顶角相等，作[DX⊥AB]，根据三角形的内角和为[180°]得到[∠BAV=∠XDQ]，从而得到[△BAV ]∽[△QXD]，再利用相似三角形的性质可求出线段[DQ]的长度。

解法7：如图10，过D作DQ⊥AC，垂足为[Q]，将[△DAQ]绕点[D]逆时针旋转[90°]得到[DA1B]，并延长[A1B]，交[AC]于点[Z]，所以[DQ=DA1]，[AQ=A1B]，[∠DQZ=∠QDA1=∠A1=90°]，所以四边形[DA1ZQ]为正方形。由解法3可得[AZ=855]，[BZ=455]。设[DQ=DA1=A1Z=QZ=x]，则[A1B=AQ=x-455]，所以[AZ=AQ+QZ=x-455+x=855]，所以[DQ=x=655]。

解法分析：“等腰直角三角形两腰相等，顶角为[90°]”的特征为[△DAQ]旋转提供了条件，同时也自然地构建了正方形，从而得到边的数量关系，借助方程思想可求线段[DQ]的长度。

基于TPACK框架下分层教学理论的解法分层，是基于图形特征和题目所给的已知条件得到的，能呈现出学生能联想的点，学生能由点到面，一步步地解决问题，能在解题中显现出清晰的解题思路。上述三个层次的解法间存在联系（如图11），加强了知识与知识之间的连接。

四、教学启示

（一）纵横相关知识，探寻解题思路

基于TPACK框架的解法分层，使得不同层次的学生，在不同的时间和空间里进行独立学习、独立思考，能够学有所获，提高能力。解题的教学价值不在于把题目的解题过程完美地呈现，而是在于通过分析题目、探究解题思路，达到弥补知识缺漏、积累解题经验、发展数学思维、提升核心素养的目的。获取题目的信息是解答好题目的前提，解题的灵感往往基于某个或者某几个已知条件，通过联想相关知识点或者作辅助线找到解题的关键点。有的学生题目没有读完就开始做题，抑或是对某些关键的已知条件敏感度不够，不能联想到相关知识和方法，其结果或答非所问，或死扣某个已知条件而忽视其他条件导致解题走偏。这就需要教师引导学生重视读题，在某些关键的已知条件处提问，强化这些条件的作用，加深学生对这些条件所引出的相关知识的理解。

（二）明晰解题策略，提升解题能力

抽象、推理、模型是数学基本思想的三个核心要素。数学是讲逻辑的，因此解题是有方向的。解一道题，需要明晰它是什么类型的问题，明确大的方向 ，再根据已知条件不断明晰具体的解题策略。例如，本文用了7种方法求解线段长度问题，从大的方向来说能求线段长度的方法有等面积法、全等、相似、三角函数、勾股定理，这里7种不同的方法是基于对已知条件不同方向挖掘得到的。在教学中，教师要注重引导学生整体把握解题方向，启发学生根据题目条件思考具体的解题策略，培养学生的创新能力；让学生通过一题多解构建知识之间的联系，体会不同的思考方向，在比较中体悟解题方法的合理性，有效掌握解题方法，提升发散思维能力。

（责任编辑 黄春香）