高中物理“摆线运动”微专题复习实践研究

［摘 要］文章深挖微专题的内涵和特点，以“摆线运动”微专题复习为例，探索如何从解决问题的不同方向入手，有针对性地引导学生抓住问题的本质、培养科学思维、建立物理模型、提炼方法形成策略，进而使学生领会物理科学思维方式，提高解决问题能力，从“学会”走向“会学”。

［关键词］微专题复习；摆线运动；建模

［中图分类号］    G633.7        ［文献标识码］    A        ［文章编号］    1674-6058（2024）17-0041-04

电磁场是高考物理的高频考点，由于电磁场的模型众多，学生建模非常困难，且不易发现问题间的内在联系，难以建立知识之间的关联性，因此电磁场部分的复习往往繁杂而低效。设计微专题引导学生复习，可帮助学生建构物理模型，把握知识之间的联系，让学生能够在多变的情境中灵活运用知识。本文以“摆线运动”为例对电磁场的复习进行探究，并利用微专题形式，帮助学生建构物理模型，领会物理科学思维方式，提高解决问题能力，让学生从“学会”走向“会学”。

一、微专题的内涵与特点

微专题的“微”，是指以一个“点”为中心，这个点可以是学生难以理解的一个概念、规律、模型。微专题教学聚焦学生不清楚的知识点，点对点地引导学生梳理知识，用时短，针对性强。

微专题的“专”，指的是对这个“微”知识点，“专”门进行深入细致、透彻的分析。微专题教学旨在循序渐进、由点及面地引导学生运用科学思维方法，定性、定量地对相关问题进行科学推理，从而找出规律、形成结论，进一步认识和体会物理模型在探究自然规律中的作用[1]。

小切口、针对性强是微专题教学的主要特征，确定有价值的教学主题是关键。教师可以结合相关考点，从学生的学情出发，将复习内容按主题进行逐级分解，从一级主题到二级主题，再到微专题，构建逻辑清晰的知识网络，优化学生的物理认知结构。例如在电磁场中“带电粒子在电磁场中的运动”就是一级主题，其二级主题包括“单电场”“单磁场”“复合场”“仪器”。在“复合场”中，“没有约束面的叠加场”是其中一个三级主题，“摆线运动”是“没有约束面的叠加场”下的一个微专题。

二、“摆线运动”微专题教学实践

“摆线运动”微专题教学的思路是首先建构数学模型，提出摆线运动的定义；其次引导学生将数学模型转换为物理模型，分析物理模型的特点和规律；最后精选6道例题，通过建构模型、变式训练等方法，使学生能够对知识进行归纳总结，并学会举一反三，将同一类问题联系起来，提炼解决问题的方法。

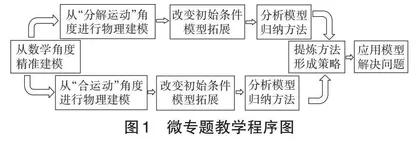
“摆线运动”微专题教学的程序图如图1所示。

（一）从数学角度精准建模

首先，提出摆线运动的定义：如图2，一个圆沿一直线缓慢地滚动，则圆上一固定点所经过的轨迹称为摆线，这种运动称为摆线运动。

其次，从数学角度推出摆线运动的轨迹方程：

[x=a（θ-sinθ）]

[y=a（1-cosθ）]

通过数学方法总结出摆线的性质：

（1）拱高：2a

（2）拱宽：[2πa]

（二）从物理角度精准建模

1.从“分解运动”角度进行物理建模

对比数学对摆线运动的定义，用运动分解的思路把摆线运动分解为匀速直线运动和匀速圆周运动来进行分析，建立物理模型，强调“配速法”的运用。下面以2018年蚌埠的一道模拟题来介绍“配速法”。

［例1］如图3所示，[xOy]坐标平面在竖直面内，[x ]轴沿水平方向，[y]轴正方向竖直向上，在图示空间内有垂直于[xOy]平面的水平匀强磁场。一带电小球从[O]点由静止释放，运动轨迹如图中曲线。关于带电小球的运动，下列说法中正确的是（ ） 。

A. [OAB]的轨迹为半圆

B.小球运动至最低点 [A] 时速度最大，且沿水平方向

C.小球在整个运动过程中机械能增加

D.小球在 [A] 点时受到的洛伦兹力与重力大小相等

解析：带电小球在“没有约束面的叠加场”中运动只受重力和洛伦兹力，且初速度为零，在这种情况下，可把速度分解成等大、反向的两个速度[v1]和[v2（v1=v2）]，如果磁场垂直[xOy]平面向里，小球带正电，它在[O]点的受力情况如图4所示，即小球的运动可以看成是以速度[v1]做匀速直线运动和以速度[v2]做半径为[a]的匀速圆周运动的两个分运动，那实际的合运动就是“摆线运动”，分别满足[qv1B=mg]，[qv2B=mv22a]。

从分运动的角度看，其匀速圆周运动的圆心在做匀速直线运动，半径不变。当小球匀速圆周运动到最低点[A]时，速度[v1]和[v2]同向，合运动的速度是最大的，受力情况如图5所示；从合运动的角度看，此时有  [qv1B+qv2B-mg=m（v1+v2）2r]，解得[r=4a]，并且由摆线运动的性质可知拱高[yA=2a]，即[r=2yA]，所以有些题目会直接告知此曲线（摆线）在最低点的曲率半径为该点到[x]轴距离的2倍。

这是最简单、最基本的情况，所以为了加深学生对摆线运动模型的理解，教师可以创设带电小球在“没有约束面的叠加场”中运动只受重力和洛伦兹力，但有水平初速度的情境，引导学生进行分类讨论。

［例2］如图6所示，一个带正电的小球沿光滑绝缘的桌面向右运动，速度方向垂直于一个水平向里的匀强磁场，试讨论小球运动的情况。

解析：将小球的速度分解为向右的速度[v01]和另一个速度[v02]，其中[v01]满足[qv01B=mg]。由于[v0]大小的具体值未知，因此存在以下三种可能：

（1）[v0=v01=mgqB]，则[v02=0]，小球直接做水平向右的匀速直线运动。

（2）[v0>v01=mgqB] ，则[v02]向右，[v01]引起向右的匀速直线运动，[v02]引起逆时针的匀速圆周运动。

这里又有三种情况：

①[v02<v01]，则在最高点，合速度向右，轨迹如图7所示。

②[v02=v01]，则在最高点，合速度为 0，轨迹如图8所示。

③[v02>v01]，则在最高点，合速度向左，轨迹如图9所示。

这三种情况小球在最低点的速度都是最大的。

（3）[v0<v01=mgqB]，则v02向左，且[v02<v01]，[v01]引起向右的匀速直线运动，[v02]引起逆时针的匀速圆周运动，这种情况是在最低点速度最大，轨迹如图10所示。

以上两道例题的配速是在一条直线上，即把合速度分解为两个在一条直线上的分速度。而2013年福建省高考理综卷第22题第（3）问的配速是不在一条直线上的。下面笔者对该题进行改编，引导学生进一步体会“配速法”。

［例3］如图11所示，空间存在一范围足够大的垂直于[xOy]平面向外的匀强磁场和沿[y]轴正向的匀强电场，磁感应强度大小为[B]，电场强度大小为[E]。让质量为[m]，电量为[q（q>0）]的粒子从[O]点以初速度[v0]沿[y]轴正向发射。不计重力和粒子间的影响，求该粒子运动过程中的最大速度值[vm]。

解析：[v0]沿[y]轴正向，与电场方向相同，把[v0]分解为一个速度[v1]，使其大小满足 [qv1B=qE]，洛伦兹力的方向和电场力相反，则[v1]的方向应沿[x]轴正方向。如图12所示，[v2]的大小满足下列关系：[v2=v20+v21]，[tanθ=v0v1]，在最高点速度是最大的，其最大值[vmax=v1+v2=EB+v20+EB2]。

例2、例3是改变了初速度的条件，可以再进一步拓展，改变粒子的受力，使其运动情况变为受到电场力、重力和洛伦兹力的“摆线运动”。

［例4］如图13所示，某空间内存在电场强度大小[E=100 V/m]、方向水平向左的匀强电场和磁感应强度大小[B=100 T]，方向垂直纸面向里的匀强磁场。一质量[m=0.1 kg]、带电量[q=0.01] C的小球从[O]点由静止释放，到达点[O′]时速率恰好为零。求：

（1）小球运动过程中的最大速率；

（2）小球运动过程中距离[OO′]的最大距离；

（3）[OO′]的长度及方向。

解析：（1）小球同时受到电场力、重力和洛伦兹力，其中电场力和重力的合力可以用等效重力代替：[mg=（mg）2+（qE）2=2]（N），[tanθ=qEmg=1]，[θ=45°]，如图14所示。在初速度为零的情况下，可把速度分解成等大、反向的两个速度[v1]和[v2（v1=v2=v）]，如图15所示，其中[v1=v]满足 [qvB=mg]，解得[v=2]（m/s），[v2= v]满足 [qvB=mv2a]，解得[a=mvqB=210]（m）。当小球圆周运动到物理意义上的最低点时，速度[v1]和[v2]同向，合运动的速度是最大的，如图16所示，有[vmax=2v=22]（m/s）。

（2）小球运动过程中距离[OO′]的最大距离：[ymax=2a=25]（m）。

（3）[OO′]的长度：[OO=vT=2πmvqB=25π]（m），方向：[θ=45°]。

这部分的教学设计思路：通过4道例题，从“只受一个恒力和洛伦兹力，初速度为零”，到“只受一个恒力和洛伦兹力，初速度与恒力垂直”，再到“只受一个恒力和洛伦兹力，初速度与恒力平行”，最后到“受两个恒力和洛伦兹力，初速度为零”，由浅入深，层层递进，帮助学生把“摆线运动”的分解方法——“配速法”的模型建构起来。

2.从“合运动”角度进行物理建模

“摆线运动”除了可用分解运动的思路，根据牛顿第二定律和运动学知识去求解，还可以用动量定理和动能定理去求解。因为洛伦兹力的大小与速度有关，所以洛伦兹力的冲量是非常有特点的。下面笔者通过两道例题来介绍解决“摆线运动”问题的第二种模型。

［例5］在磁感应强度为[B]的匀强磁场中，一质量为[m]、带正电[q]的小球在[O]点静止释放，小球的运动曲线如图17所示，重力加速度为[g]。求：

（1）小球运动到任意位置[P（x，y）]处的速率[v]；

（2）小球在运动过程中第一次下降的最大距离[ym]和此时的曲率半径[r]；

（3）当在上述磁场中加一竖直向上、场强为[EE>mgq]的匀强电场时，小球从[O]点静止释放后获得的最大速率[v′m]、上升的最大距离[y′m]和此时的曲率半径[r]。

解析：（1）带电小球只受重力和洛伦兹力，而洛伦兹力不做功，只有重力做功，所以根据动能定理有[mgy=12mv2-0]，解得[v=2gy]。

（2）如果第一次下到最低点，则根据动能定理有：

[mgym=12mv2m-0]

每一瞬间的受力如图18所示，根据动量定理，水平方向有：

[qvyB·Δt=m·Δvx]，

可以用微积分的思路求解，即[qB（vy1Δt1+vy2Δt2+vy3Δt3+…）=m（Δvx1+Δvx2+Δvx3+⋅⋅⋅）]或者[qvyB·Δt=m·Δvx]，直到小球下到最低点，[vyΔt=ym]，[Δvx=vm-0]，所以有[qBym=mvm-0]，

联立解得[ym=2m2gq2B2]，[vm=2mgqB]，