问题让数学思维在课堂教学中生根

［摘 要］课堂不仅是知识传授的场所，还是思维培育的沃土。教学核心在于培养思维。数学思维的培养离不开问题的提出、分析和解决。因此，利用问题引导学生数学思维的发展是数学课堂教学的一个重点。文章以“菱形的性质与判定”教学为例，探讨如何通过问题驱动，使学生在掌握概念知识的同时发展数学思维。

［关键词］问题驱动；数学思维；菱形的性质与判定

［中图分类号］    G633.6        ［文献标识码］    A        ［文章编号］    1674-6058（2024）29-0015-03

《义务教育数学课程标准（2022年版）》（以下简称《数学课标》）提出，探索在不同的情境中从数学的角度发现和提出问题，综合运用数学和其他学科的知识从不同的角度寻求分析问题和解决问题的方法，能够回顾解决问题的思考过程，反思解决问题的方法和结论，形成批判性思维和创新意识。《数学课标》强调，课堂教学应以培养学生思维为核心任务，超越单纯的知识传授。

传统教学中，教师过于强调知识技能的应用，导致学生的思维停留于浅表层次。偏重应试的课堂教学，易使学生的思维僵化、封闭。为有效发展学生的数学思维，提出问题、分析问题和解决问题必不可少。在“菱形的性质与判定”教学中，笔者尝试采用问题驱动法，让学生在解决问题的过程中既掌握新知，又发展数学思维。

一、教学过程

（一）设置问题，引出新知

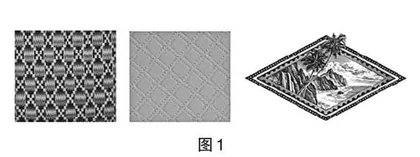
问题1：以下几张图片（如图1）都含有一些平行四边形，观察这些平行四边形，你发现它们有什么样的共同特征？

追问1：你能用自己的语言给这些具有共同特征的图形命名吗？

追问2：你能给这些图形下定义，并猜想它有哪些特殊的性质吗？

师生活动：教师提出问题让学生独立思考。针对两个追问，建议学生分组讨论，通过“观察—猜想—验证”的过程，引导学生得出菱形的定义。教师板书：①找特征；②下定义；③得出包含关系（用椭圆形来表示）；④猜想菱形的特殊性质。

设计意图：通过观察相应图形的特征，促使学生运用度量工具或其他手段进行发现和猜想，体现数学学习“观察—猜想”的基本过程。鼓励学生用自己的语言给具有共同特征的图形命名，从而使学生获得新知识，培养他们的语言表达能力和符号意识。此教学设计立意高远，聚焦于思维发展，引导学生探究菱形的独特属性。

（二）实验操作，概念论证

安排学生事先准备好一个用纸折成的平行四边形（如图2），并回答下列问题。

问题2：如何把这个平行四边形折成一个菱形？（图3）

问题3：观察折好的菱形，回答以下问题。

（1）你能找出菱形具有而平行四边形不具有的特征吗？

（2）菱形是对称图形吗？

（3）你能用数学语言描述这些特征并简要分析其正确性吗？

师生活动：教师引导学生用不同的方法将事先准备好的平行四边形折成菱形，观察菱形的特征，并分享自己的观察结果。

设计意图：本环节旨在让学生通过亲手操作，直观认识菱形的独特性质。学生通过观察、操作以及猜想得出菱形的特殊性质。折纸活动不仅丰富了学生的直观感受，还提升了他们的操作能力，有助于培养学生的几何直观素养。此教学设计从智力因素角度，为学生提供了锻炼具象思维的有效途径；而从非智力因素角度，则有效激发了学生的学习动力。

通过折纸与追问活动，学生初步得出结论：菱形是轴对称图形，四条边相等，对角线互相垂直。

问题4：所得出的这些特征是否准确？

已知：如图4，在菱形[ABCD]中，[AB=AD]，对角线[AC]与[BD]相交于点[O]。求证：（1）[AB=BC=CD=AD]；（2）[AC⊥BD]。

师生活动：引导学生从他们总结的多个特征中提炼出精练且有代表性的进行验证。验证结束后，利用几何画板展示菱形的性质。

设计意图：虽然学生已经得出了一些特殊结论，但这些结论以猜想为主。问题4旨在促使学生通过演绎推理证实结论的正确性，锻炼学生的推理能力，培养学生的验证习惯和思维的严谨性。借助几何画板，从多个角度论证菱形的相关特征，帮助学生进一步明确菱形的基本性质。

（三）典型例题，方法提炼

问题5：如图5，已知菱形[ABCD]中[BD=6]，如果要求出[AB]的值，还需要增添哪些条件？

生1：可以添加[AC]的长度。

生2：可以添加[∠BAD]或[∠ABC]的度数（最好是特殊角）。

生3：可以添加菱形的周长或面积。

……

学生的答案五花八门，教师将这些答案写在黑板上，随后与学生共同分析哪些答案是同一类型，哪些条件是有效的。最后，对筛选出来的有效答案进行归纳总结。

设计意图：问题5作为一种开放性不良题型，旨在促使学生超越仅分析并解决已有问题的阶段，激励他们主动提出与目标相对应的问题，从而将不良题型转化为完整题型。由于结论的指向性明确，因此学生的回答并不是无序的。此问题的设置有助于学生深入理解题目条件与结论之间的关系，同时对培养学生的创新意识有较大的帮助。

问题6：如图6，在菱形[ABCD]中对角线[AC]和[BD]相交于点[O]，[∠BAD=60°]，[BD=6]，求菱形的边长[AB]和对角线[AC]的长以及菱形[ABCD]的面积。

追问1：你能求出此菱形的高吗？

追问2：关于与菱形相关的计算，你能总结出哪些主要方法？

生1：可以把菱形转化为直角三角形。

生2：可以利用勾股定理来求解。

生3：可以利用三角形全等来求解。

……

师生活动：根据问题5中某位学生的回答设计问题6。在解答问题6后，紧接着进行追问。其中，追问2旨在引导学生通过合作学习，学会梳理方法、总结问题的通性通法。

设计意图：问题6旨在激发学生的学习热情。随后的追问则促使学生多角度思考问题，使学生认识到不同条件会导致不同结论，为学生把握知识间的联系奠定基础。问题解决后，引导学生梳理菱形性质应用的基本方法，目的是通过整理解决此类问题的基本方法和步骤，培养学生的总结归纳能力。

（四）应用深化，知识融合

问题7：如图7，在平面直角坐标系[xOy]中，若菱形[ABCD]的顶点[A]，[B]的坐标分别为（-3，0），（2，0），点[D]在[y]轴上：

（1）求点[C]的坐标；

（2）连接[AC]和BD，求[AC]和[BD]的长度；

（3）求菱形[ABCD]的面积；

（4）直线[AC]与[y]轴的交点为[E]，与[BD]的交点为[F]，求线段[EF]长度。

学生活动：先独立思考，随后合作探讨解答，互相检验步骤的正确性。

设计意图：菱形的知识常在解答题中和其他图形结合考查，将菱形融入坐标系，有助于学生更好地理解知识，为学生提供多元思维路径，强化学生几何与代数的融合意识，培养学生的几何直观素养和模型观念。

二、教学反思

（一）问题驱动，激发学习兴趣

当前课堂教学中，问题设计常呈现“零散”和“封闭”等弊端，“零散”导致思维不连贯，“封闭”使问题缺乏探索空间。此类问题多聚焦于知识应用，而与思维培养关联不大，应试倾向明显，难以激发学生的学习兴趣。

本节课，笔者设计了一系列层次分明、结构紧凑的问题，不仅调动了学生的生活常识，还引导他们结合生活经验与学习经验建构菱形的数学模型，并应用于实际问题解决。这些问题环环相扣，不仅深化了学生对菱形的认识和理解，还提升了他们解决实际问题的能力以及分析、归纳、总结等能力。更重要的是，在问题的驱动下，学生的数学思维得到了有效发展。

（二）问题拓展，搭建知识桥梁

笔者设计一系列问题，引导学生经历问题的提出、分析及解决过程，从而深刻领会知识核心。这样的教学方式不仅能促进知识学习，还有助于思维培养。在本节课中，学生思维在解决问题的过程中持续动态变化。所设计的问题促进了师生互动与生生互动，使学生的思维保持活跃。通过问题的不断拓展，学生得以深入理解菱形的概念、性质及掌握相关知识的应用，有效搭建了静态知识和动态思维之间的桥梁。

（三）问题解决，激活思维

数学课堂教学主要通过提出、分析和解决问题来培养学生的思维能力。本节课，笔者设计了一系列问题，旨在让学生通过解决问题理解和掌握相关知识，并进一步认识这些知识的应用方向及其与其他知识的联系与融合。随着问题的不断提出与解决，学生的思维始终保持活跃。

在数学课堂教学中，随着问题的不断解决，学生的数学思维稳步发展。同时，“做中学”和“思中学”的教学模式有助于学生思维的培养和学习的深入。

［   参   考   文   献   ］

[1]  顾明远.课堂教学是培养思维的最好场所[J].基础教育论坛，2018（36）：62.

[2]  中华人民共和国教育部.义务教育数学课程标准：2022年版[M].北京：北京师范大学出版社，2022.

[3]  许礼光，沈琼.高层次数学思维的培养路径[J].数学通报，2019（5）：33-36，39.

[4]  邱志刚.让问题摇动问题，让题干枝繁叶茂：一堂几何复习课的思考[J].中学数学研究（华南师范大学版），2021（24）：5-8.

[5]  陈竺.问题引导：重构初中数学教学新范式[J].中学数学教学参考，2021（33）：26-27.

[6]  郅庭瑾.为思维而教[M].北京：教育科学出版社，2007.

（责任编辑 黄春香）