理想气体状态方程的多维进阶推导探究

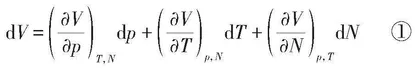
［摘 要］文章多维度深入推导与讨论理想气体状态方程，旨在帮助一线教师更深刻地理解热学问题的基本处理方法。同时，从高中与大学物理知识衔接的视角宏观把握处理热学问题的高阶思维，为提升学生的物理学科核心素养提供有益参考。

［关键词］理想气体状态方程；气体实验定律；麦克斯韦速度分布律

［中图分类号］    G633.7                ［文献标识码］    A                ［文章编号］    1674-6058（2024）32-0037-03

随着2025年四川省新高考政策的调整，选择性必修第三册的热学内容被正式纳入高考范围。由于此前该内容非高考重点，教师对其理论架构、教学要点及考查方式了解不深，特别是对热学核心——理想气体状态方程的理解需进一步加强。理想气体状态方程是热学的核心知识点，其重要性不言而喻。人教版和教科版教材均重视其推导，并特设章节详细阐述利用不同气体实验定律推导理想气体状态方程的方法。这样多样化的推导路径为学生提供了多元化学习视角。然而，从专业物理教师视角看，仅掌握推导过程远远不够。为更好地培养学生的物理学科核心素养，提升学生的高阶思维能力，需将高中与大学物理知识有机衔接，从更高层面来深入探讨理想气体状态方程。基于此，本文多维度深入推导与讨论理想气体状态方程，旨在为教师提供全新教学视角，为提升学生的物理学科核心素养提供有益参考。

一﹑用气体实验定律推导

（一）具体推导过程

根据玻意耳定律、盖吕萨克定律以及阿伏伽德罗定律，我们可以得出气体的体积随压力、温度以及气体分子数的变化而变化，表述为：

[V=V（p，T，N）]

左右两端求微分可得：

因为研究对象是一定量的气体，所以分子数目是一定的，因此①式中的第三部分为0。

两边同时积分得：[lnV+lnp=lnT+C]，令[C=lnR]，为方便计算，将一定量气体设为1 mol，此时[V=Vm]，整理可得[pVm=RT]，两边同乘物质的量[n]，则可得：[pV=nRT]。证明完成。

（二）理想气体常数R的计算

理想气体状态方程中，R是理想气体常数，亦称普适气体常数，其数值是基于标准状况下1 mol气体计算出来的，与气体种类无关，只与单位有关。因此，不同单位下R的数值是不同的。目前，通用的主要有两种，一是用国际计量单位计算出的[R=8.314 J·mol-1·K-1]，二是在1atm下计算出的[R=0.082atm·L·mol-1·K-1]。

当[p=101325 Pa]，[V=22.414 L=0.022414 m3]，[T=273.15 K]，[n=1 mol]时，代入数据得：

二﹑用理想气体压强初级微观理论推导

（一）理想气体的微观模型

实际微观粒子间存在相互作用，短程时表现为强排斥力，长程时则相互作用力较弱，且粒子具有体积，非质点。在标准状态下，1 mol气体是[V=22.4 L]，[n=6.02×1023]个，分子间的平均距离[l=3.34×10-7cm]，而气体直径约为[10-8cm]，故对于温度较高、压强较小的情况，可将具有以下特性的微观粒子视为理想气体。

（1）组成气体的微观粒子都是质点，并遵从牛顿力学定律。

（2）粒子间除碰撞瞬间外，无其他相互作用。

（3）粒子间及粒子与容器的碰撞都是完全弹性碰撞。

理想气体的压强微观本质上可理解为大量分子在单位时间内对单位器壁面积施加的平均冲量。

（二）长方体容器中的气体

（1）一个分子碰撞器壁时，给予器壁的冲量为[Iix=2mυix]。

（2）[dt]时间内运动到[dS]并与器壁发生碰撞的分子数，如图1所示：体积[Vi=υixdtdS]，设单位体积内具有速度[υix]的分子数密度为[ni]，[dt]时间内具有速度[υix]且与[dS]碰撞的分子数为[N=Vini=niυixdtdS]。

（3）具有速度[υix]的分子给予器壁总冲量为[Ii=2miυixN=2miυ2ixnidtdS]。

（三）球形容器中的气体

壁后法向冲量[I=2mυicosθ]，距离下一次碰撞器壁时间差为[2Rcosθυi]，单个气体分子单位时间内碰撞器

三﹑用麦克斯韦速度分布律推导

（一）用麦克斯韦速度分布律推导

我们通过麦克斯韦速度分布律来进行严格推导。设[x]方向的麦克斯韦速率分布函数为[f（υx）]。选择一个平面[dS]，并设垂直于该平面的方向为[x]方向，同时规定面向平面的方向为正方向，则对于速度分量在[υx]附近的分子产生的压力[dF]=单一分子的贡献压力×单位体积内这种分子的数目×体积，即[dF=2mυx·nf（υx）dυx·υxdSdt]，其中[n]是单位体积内的分子数目。整理得[dF=2nmυxυxf（υx）dυxdSdt]，

由于只有面向平面的分子才能撞到平面上，因此上式对[υx]从零积分至正无穷有：

（二）温度的统计意义

（1）理想气体温度是系统内部分子无规则热运动的剧烈程度。

（2）温度是大量分子热运动的集体表现，含有统计意义。

四﹑用统计物理方法推导

五﹑结语

本文以理想气体状态方程的进阶推导为例，遵循由低阶到高阶的教学原则，通过大中衔接的四个维度，深化了师生对理想气体状态方程的理解。本文阐述了物理学理论的进阶发展，为物理学习和研究提供了理论框架与丰富素材，旨在逐步消除学生在物理思维上的障碍，培养他们的物理认知能力和学科意识，并构建稳固的学科逻辑体系。通过具体项目实践，本文进一步实现了物理学科核心素养的培养目标。

［   参   考   文   献   ］

[1]  汪志诚.热力学·统计物理[M].6版.北京：高等教育出版社，2020.

[2]  李椿，章立源，钱尚武.热学[M].3版.北京：高等教育出版社，2015.