立足单元视角　提升核心素养

［摘 要］以北师大版数学教材四年级下册“小数的意义和加减法”单元为例，立足单元视角，梳理单元目标，设计分层、弹性和个性化的作业，以凸显数学本质，帮助学生整体建构知识。这样可促使学生的学习真正发生，助力学生的单元整体学习，发展学生的数学核心素养。

［关键词］作业设计；核心素养；单元视角

［中图分类号］ G623.5 ［文献标识码］ A ［文章编号］ 1007-9068（2024）12-0001-04

作业是教学过程中的一个重要环节，在巩固知识、训练技能等方面起重要作用。但是，许多教师设计的作业出现了形式单一等情况，导致学生对完成作业不感兴趣，最后影响学生的数学学习。《义务教育数学课程标准（2022年版）》（以下简称“数学新课标”）强调单元整体教学。这就要求教师依据数学新课标和单元教学目标，深入钻研教材，梳理单元主题，通过分析、整合、重组等方式进行系统规划和整体作业设计，围绕单元主题确定作业内容，以促进学生对单元知识的理解与掌握，提升学生的数学核心素养。

单元作业是学生日常学习中不可或缺的有机组成部分，既是教师巩固教学效果的重要手段，又是发展学生素养的主要途径。如何基于“双减”政策设计分层、弹性和个性化的作业，是广大数学教师需要深入研究的问题。下面，笔者以北师大版数学教材四年级下册“小数的意义和加减法”单元整体作业设计为例，阐述具体做法。

一、基于单元内容定目标

在设计单元作业之前，教师要深入解读数学新课标和教材，梳理单元知识结构，提炼单元主题，对单元作业进行整体规划，以确立单元作业目标，明晰单元作业设计的整体思路，让单元作业涵盖本单元所有的重要知识点。同时，要将单元教学目标作为单元作业设计的基点，使学生通过完成作业建立学科知识结构，巩固所学的知识和训练可迁移的思维，实现核心素养的发展。

例如，笔者在教学北师大版数学教材四年级下册“小数的意义和加减法”这一单元时，确定了如下的单元作业目标（见表1）。

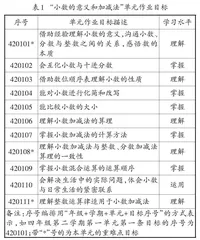
表1   “小数的意义和加减法”单元作业目标

[序号 单元作业目标描述 学习水平 420101* 借助经验理解小数的意义，沟通小数、分数与整数之间的关系，感悟数的本质 理解 420102 会互化小数与十进分数 掌握 420103 借助数位顺序表理解小数的性质 理解 420104 能对小数进行化简和改写 掌握 420105 能比较小数的大小 掌握 420106 理解小数加减法的算理 理解 420107 掌握小数加减法的计算方法 掌握 420108* 理解小数加减法与整数、分数加减法算理的一致性 理解 420109 掌握小数混合运算的运算顺序 掌握 420110 会解决生活中的实际问题，体会小数与日常生活的紧密联系 运用 420111* 理解整数运算律适用于小数加减法 理解 备注：序号编排用“年级+学期+单元+目标序号”的方式表示，如四年级第二学期第一单元第一条目标的序号为420101；带“*”号的为本单元的重难点目标 ]

上表立足数学新课标，较全面地涵盖本单元的知识点，具有关联性、整体性和结构性的特点，旨在帮助教师梳理单元作业目标，整体把握单元作业设计，巩固学生对小数计数单位的认识，理解小数加减法与整数、分数加减法算理的一致性。这样设计单元作业，有助于培养学生的数感和运算能力，提高学生解决与小数加减法相关的实际问题，形成应用意识；同时，能更好地落实育人价值，发展学生的核心素养。

二、依据单元目标定内容

单元作业目标制订后，要思考如何通过层次性、系统性、整体性的作业，将整个单元的教学内容细化，让目标与内容契合。这样可以深化学生对单元知识的理解，促进学生高阶思维的发展，实现提升学生核心素养的目标。数学新课标在第二学段的“教学建议”中指出：“在认识整数的基础上，认识小数和分数。通过对数的认识和数的运算有机结合，感悟计数单位的意义，了解运算的一致性。”“小数的意义与加减法”单元包含了数的认识与数的运算等内容，进行单元作业设计时要注重学生对数学本质的理解，帮助学生形成体现整体的知识网络。

（一）数的概念——感受延续性

小数（十进制分数的改写）是整数领域外的一类数，是数概念的一次扩充，是学生数学思维的一次飞跃。小数与整数的意义相同，都是计数单位及个数的表达。引导学生能顺利地从整数的认识迁移到小数的认识，能从形式模仿走向意义理解，实现小数意义的整体建构，这是小数意义学习的本质所在。正如张奠宙教授所说的：“小数的本质在于‘位置计数法’的拓展，而不在于‘十分之几’的表述。小数是将个、十、百、千等不断扩大的位置计数方式，朝着另一个方向（‘不断缩小’的位置计数方式）加以延伸，即增加了十分位、百分位等新位置，使之成为更为完善的一种位置计数制度。”基于此，设计本单元的作业时，需要体现小数概念的本质。

作业1：看图答题。

（1）下图中可以表示0.3的是（   ）。

[D.][C.][B.][A. ][ ] [十位][个位][十分位][百分位][千分位] [0][1]

（2）请用你喜欢的方式或语言来表示0.03、0.003和3。

作业1的设计，目的是结合直观模型辨析小数的意义，明确整数、小数计数的一致性，即“十进位值”计数；借助多元表征将小数计数单位关联整数计数单位，形成系统，即表达计数单位及个数的多少，直观感知“位值”，发展学生的数感；通过对0.03、0.003和3的表达进行对比，让学生明白小数和整数的本质是一脉相承的，进一步加深学生对小数意义的理解。

（二）运算内在联系——体会一致性

学习小数加减法之前，学生已经掌握了整数加减法的竖式计算方法、整数的四则运算、整数的运算定律等。教学小数加减法时，教师要立足学生已有的知识经验，找准新知识的生长点，引导学生将整数加减法迁移到小数加减法的学习中，理解并掌握小数加减法的算法和算理，体会数运算的一致性，发展学生的运算能力和推理意识。因此，进行“小数的意义和加减法”单元作业设计时，教师要考虑如何才能让学生感悟到运算之间的联系，体会数运算的一致性，即相同数位或分数单位才能相加减。为此，笔者设计了一道探索与总结整数、小数、分数加减法相同点的题（作业2）。

作业2：看算式，写算理。

[（1）

（2）

（3）

我发现：整数、小数、分数加减计算方法的相同点是

。

][1-[25]=  [55]-[25]  =[35]] [转化][小数点对齐][个位对齐][1 3 3

5 6] [1 8 9][+] [4 . 5

2 . 3 3] [2 . 1 7][-]

作业2通过整体设计整数、分数、小数的加减法笔算算式，帮助学生在观察中建立小数与整数、十进分数之间的联系，感知小数加减法与整数、分数加减法是一脉相承的，都是计数单位的个数相加减。这样的作业有助于凸显运算本质，让学生理解算理的一致性。

（三）整体建构——体验发展性

单元作业要注重结构化设计，帮助学生建构单元整体框架，让知识在交融中得到内化。为此，笔者以气泡图和集合图的形式设计了作业3。

作业3：利用双气泡图或集合图比较小数加减法与整数加减法的计算方法。

作业3借助气泡图和集合图沟通小数加减法与整数加减法的相同点和不同点，使学生进一步理解算理与算法，体会数运算的一致性。通过单元整体建构，将小数加减法和整数加减法的特点相互交融，促使学生走向深度学习。

三、根据核心素养定形式

单元作业设计要基于学生的智力、兴趣、能力等因素，既要使作业有梯度，让所有的学生都能达成基础性目标，也要让学习能力强、兴趣广的学生可以选择挑战性作业，提高自身的综合素养。笔者根据布鲁姆教育目标分类理论，从“注重差异性，作业层次化”出发，一共设计了基础巩固、能力拓展和综合应用三类作业，在内容上指向高阶思维的培养，促使学生的“四基”“四能”获得同时发展。

（一）基础巩固类作业——精

“双减”政策下，基础巩固类作业旨在巩固学生的基础知识和基本技能，所以要体现出“精”的特点，即让学生的练习更加精练，并适当梳理与完善单元知识的建构过程，深入理解数学的本质。故而，笔者设计了作业4。

作业4：下图是淘气和爸爸妈妈周末去超市的购物小票，请根据小票内容填好下面的统计表。

[店号： C0037  2022/03/18   19：45：41

收银机： JM26         小票号：  045276

收银员： CB727758   类型： 零售销售

商品名称               数量            单价     成交价

精品超市购物袋大号

6945854147544 1 0.30

向龙食茶叶蛋

2315522455712 1 11.51

金锣精致风味红肠135g

6579425745524 1 6.80

水晶红富士

2456879154721 1 15.46

火焰红葡萄

2313251542541 1 16.27

火龙果

2354651841571 1 25.58

养乐多活菌型乳酸菌饮品100ml

6578491254261 2 23.40

蒙牛风味酸奶饮品

6578492215214 2 26.70

青椒

3516225411415 1 8.54

西红柿

5684972321521 1 9.73

应收： 144.29 件数：  12

实收：        200.00            找零：  55.71

会员账号： 1758425652266412]

[ 熟食类 蔬菜类 水果类 饮料类 价钱 ]

（1）比一比，哪一类用的钱最多？最多的比最少的多多少钱？

（2）请选用合适的数据自编一道运用运算定律解决问题的题目，并解答。

（3）用自己喜欢的方式绘制一幅统计图。

作业4意在结合真实情境，发展学生的数据意识；通过统计，掌握比较小数大小的方法；自编题目并解决问题，体会运算定律在小数中也同样适用；绘制统计图，培养学生的作图能力。

（二）能力拓展类作业——实

这类作业主要发展学生的认知能力和思维能力，故要体现出“实”的特点，即着重发展学生的推理意识和创新意识。由此，笔者设计了作业5。

作业5：依次计算。

假设 A=0.02，B=0.16，那么A+B=      。

A=0.002，B=0.016，那么A+B=      。

A=0.0002，B=0.0016，那么A+B=      。

假设A=                   ，B=                   ，那么A+B=      。