以纵向求联统整数学教学的整体性与一致性

［摘 要］《义务教育数学课程标准（2022年版）》特别强调数学课程的整体性与一致性，力求打通不同学段学习之间的关联。基于纵向求联进行数学教学，旨在以数学知识的内在逻辑联系为起点，用联系的观点为学生构建数学学习的基本思路，使学生在横向的数学知识积累上，纵向深化数学思维的发展。以“稍复杂的组合问题”的教学为例，通过对照、比较、抽象、提炼等方式，发展学生纵向求联的思维能力，促进其思维水平的提高，完善学生的认知结构，实现数学教学的整体性与一致性。

［关键词］统整；数学教学；纵向求联；整体性；一致性

［中图分类号］ G623.5 ［文献标识码］ A ［文章编号］ 1007-9068（2023）30-0001-05

《义务教育数学课程标准（2022年版）》指出数学课程内容的一大特点就是整体性，这是教学实践中应当突出的核心内容，要求呈现不同数学知识之间的实质性关联，展现内容与观念之间的融合，体现课程内容的整体性。郑毓信教授提出数学教学中“求联”的观点，即用联系的观点对学习目标、学习程序、学习内容、学习方法等数学学习中的诸多元素进行组合与排序，形成单向或多向的线性和网状认知建构，实现学生知识结构的掌握和思维品质的提升，这和《义务教育数学课程标准（2022年版）》对数学课程整体性与一致性的要求相符合。在以往的数学课堂中，教师多以横向求联的观点进行教学，虽然横向求联重视知识的结构性和关联性，从单向呈现走向多向关联，但是容易出现学生被动关联、形式关联等问题。相比于知识简单积累的横向求联，纵向求联更加重视在教学中通过具有递进关系的对象，将其系统化联系，以提炼对象之间的本质特征，这对完善学生的认知结构和提升其思维水平、实现数学教学的整体性与一致性更有优势。

为引导学生经历数学知识的发生、发展过程，建立生活与数学以及不同数学知识之间的联系，体会数学知识的本源性、一致性与整体性，笔者在“稍复杂的组合问题”一课教学中，基于纵向求联展开了一系列的思考与实践。

【课前思考】

“稍复杂的组合问题”是人教版数学教材三年级下册“搭配（二）”第三课时的内容，属于排列组合知识范畴。排列组合知识在日常生活中应用广泛，其思维方式也与二年级上册中有序思考、连线表示、用不同数字组合多位数的知识和思考问题方式有关，同时也为后续统计与概率知识的学习奠定基础。本节课围绕“找出四支球队的比赛（每两队赛一场）次数”这一生活实际中的问题，让学生在初步感知排列组合知识的基础上，通过更简洁、更抽象的表达方式，掌握稍复杂的组合问题中所包含的抽象的排列组合知识，进一步发展学生的数感、符号意识、运算能力和推理能力，促进学生数学核心素养的提升。

但是，在以往的教学实践中也发现了一些问题：大多数学生无法用数学方式表达思考过程和呈现解决问题的结果，缺乏有序和全面思考问题的能力，如学生较少运用图解法、列表法等简洁的数学思维方法解决问题。一方面，相较于直接数的方法，运用图解法、列表法等数学思维方法相对烦琐；另一方面，学生缺少对数学思维方法的元认知。同时，还有一部分学生会直接用列算式的方法来解决问题，并且能解释算式的原理。另外，学生知识基础和思维水平的参差不齐，也给本节课教学带来了一定的挑战。在解决实际问题过程中，如何运用抽象的、多样化的解题方法，如排除法、列举法、连线法、列表法等，引导学生有序思考，清晰、有条理地阐述自己的想法？如何引领学生在横向、纵向比较各种方法中寻找联系，体会到“思维层次有别，但方法相通、意义相同”呢？让学生的数学思维有所发展是本节课教学的重点，且学生在解题方法上的梳理、比较、反思、深化，对他们后续的数学学习也起到积极作用。

基于以上思考，将本课的教学目标制订如下。

1.结合生活实例，理解“比赛场次”这一类稍复杂的组合问题，并能运用连线、画图、列表等方法解决问题。

2.经历解决“比赛场次”问题的探索过程，进一步学会从整体出发，形成有序、合理的数学思维方法，积累数学活动经验。

3.通过问题解决，感受到数学与现实生活的密切联系，在问题解决的过程中，体会生活数学与抽象数学之间的一致性。

【课堂实录】

以解决“比赛场次”问题为主线展开：四人小组，一个人要比几场→每个人分别比几场→整个小组共赛几场→交流、分析方法→五人小组一共握手几次→9人拍照一共几张（优化）。

一、前设铺垫：游戏激趣，唤醒经验

（一）课前游戏，激活经验

游戏要求：四人小组友好握手，每两人握手一次，相互道“你好”。

师：（随机采访学生）你握了几次手？

……

【设计意图】 采用课前游戏的方式，让学生在握手中感受每人握几次，为后续的学习积累原始经验。同时，让学生对“比赛场次”这样的组合搭配模型有初步感知，体会数学与生活之间的联系，为寻找生活中的模型做好准备。

（二）回归生活，提出问题

师：学校举行乒乓球比赛，小方、小王、小李、小林分到同一个小组，要求每两人进行一场比赛。面对这样的信息，你能提出什么问题？

生1：小方在小组赛中要打几场？

生2：整个小组共赛几场？

大屏幕呈现：小方、小王、小李、小林参加乒乓球比赛，被分到同一个小组，要求每两人进行一场比赛。小方在小组赛中要打几场？整个小组共赛几场？

……

【设计意图】 教材提供的“三年级4个班进行足球赛”这一学习素材，虽然具有很强的现实性，也贴近学生的实际生活，但是在解决问题的过程中，学生倾向于直接用数学序号代表班级，无法更好地体会符号代表的简洁性。因此，选择具有相同模型的乒乓球比赛问题，并通过握手游戏的铺垫，帮助学生更好地理解情境中的问题。

二、分析思考：解决问题，方法多样

（一）初步探索，解决问题

师：小方在小组赛中要打几场？你能在纸上表示出来吗？

（学生独立思考，教师巡视，选择部分学生的作业在大屏幕上展示，预计学生会出现以下方式）

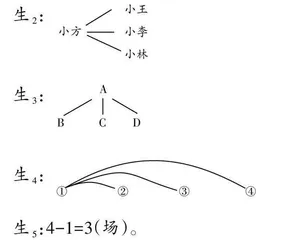
生l：小方——小王，小方——小李，小方——小林。

生5：4-1=3（场）。

师：（问生1）你在每两人之间画一条横线，表示什么意思？

生1：在小方和小王之间画一条横线，表示小方和小王要打一场比赛。因此，三条横线就表示小方要打三场比赛。

师：用一条短横线表示两个人打一场比赛，非常好。

师：（问生3）这里的A、B、C、D表示什么意思？

生3：A表示小方，B表示小王，C表示小李，D表示小林。

师：同学们，你们觉得他的表示方法好吗？好在哪里？

生6：简洁、方便。生4用数字表示四位同学，也很简便。

师：在解决问题的时候，用字母、符号表示具体的事物简洁方便。

师：我对生5的方法很感兴趣，请这位同学来介绍一下自己的想法。

生5：因为小方不用跟自己比赛，而是跟另外三人比赛，所以减去1，就是减去小方与自己比赛的场数。

师：是的。自己不能跟自己比赛，应该减去1。

师：（指着前四种方法，最后停在生2的方法上）大家看，这四种方法在表示的时候都有一个优点，你们觉得是哪一点？

生7：都是先从小方开始思考，再从小王到小李，最后到小林，非常有顺序。

师：是啊！有序思考是一个非常好的思维品质，希望大家都能具备。

……

【设计意图】对于“一个人比赛几场？”的问题，学生能顺利解决，但由于他们的生活经验与知识基础存在差异，所以解决问题的方法在具体表现形式上也会不同。展示学生在独立思考中产生的不同方法，既让学生体会到方法的多样化，又体会到多样化方法之间的共性；既让学生体会到有序列举的优势，为一些知识基础相对薄弱的学生理解和解决后继问题打下基础，又通过解读一些特殊的方法，消除学生的困惑，有助于学生形成自己的解题方法。

（二）制造冲突，引出问题

师：大家刚才都关心小方，现在来关心一下另外三位队员。在整个小组赛中，小王、小李和小林分别要打几场比赛呢？请学着生2的表示方法，交流汇报。

师：我们看到，小方要比赛3场，小王要比赛3场，小李要比赛3场，小林也要比赛3场，那整个小组赛打完共要多少场？

生11：12场，三四十二。

生12：不对，有重复，没有12场。

师：请用自己喜欢的方式来解决“四人小组比赛完共需几场”的问题，要求不重复。

……

【设计意图】对于“四人小组比赛完共需几场”的问题，学生会出现分歧。通过引导学生发现矛盾所在，引发学生进一步思考问题解决的策略。

三、纵向求联：对比交流，深化思维

（一）独立思考，呈现方法

（学生独立思考，教师巡视，选择各种方法呈现在黑板上，按一一列举法、连线法、图式法、算术法等分类，同时预计学生可能会出现以下解题方法）

生4：3+2+1=6（场）。

生5：3×4=12（场），12÷2=6（场）。

生6：3×4=12（场），12-3=9（场）。

（列表较复杂，估计列表法不可能有学生运用）

（二）交流想法，获得启发

师：（在学生独立思考后）现在同学们都已经有了自己的想法，请把自己的想法跟旁边的同学进行交流。

（三）分析梳理，博采众长

师：解决问题的方法有很多，如生1采用一一列举的方法，生2用连线表示的方法，生3用图示的方法，后面几位同学用列算式的方法，我们还可以用列表法来解决问题。（在相应方法的后面板书：一一列举法、连线法、图示法、算式法、列表法）我们先请生1上前来介绍他的方法。

生1：（指着板书）小方和小王、小李、小林比赛3场；到小王的时候，由于已经和小方比赛过了，所以与小李、小林比赛2场；到小李的时候，由于已经和小方、小王都比赛过了，所以只要和小林比赛1场；最后，小林和另外三位都比赛过，就不用画出来了。

师：他汇报时有一个优点，就是已经比赛过的场次不重复表示了。

师：接下来，请生2上前来介绍他的方法。

生2：（指着板书）写数字方便，所以用①②③④分别表示小方、小王、小李、小林。先是①和②、①和③、①和④共比赛三场，然后是②和③、②和④比赛两场，最后是③和④比赛一场，总共比赛6场。我也和生1一样，已经连线过的比赛场次就不重复连线了。

师：生2用四个数字表示四位同学，非常简便；同时，用连线表示一场比赛，很清晰。

师：接下来，请生3上前来介绍他的方法。

生3：（指着板书）我是用字母A、B、C、D分别表示四位同学，中间用直线连接，表示两个人进行一场比赛。首先连线AB、AC、AD，共三场；然后连线BC、BD，共两场；最后连线CD，一场。

师：为了让大家看得更清晰，老师用三种颜色的粉笔再描绘一遍生3说的连线。

师：还有同学用一个算式就表示出了比赛场次，请他也上来介绍自己的方法。

生4：3表示小方跟小王、小李、小林比赛了三场，2表示小王跟小李、小林比赛了两场，1表示小李跟小林比赛了一场，所以一共比赛了6场。

师：你在介绍自己方法的时候，眼睛却看着别人的图示法，那能借着别人的图示，再介绍一遍你的方法吗？

生4：（借用生1的图示）3表示小方跟小王、小李、小林比赛了三场，2表示小王跟小李、小林比赛了两场，1表示小李跟小林比赛了一场，所以一共比赛了6场。